北沟林场华北落叶松生物量模型的研究
姜 鹏,董树国 ,隋玉龙 ,王骄洋,王桂真
(1. 河北农业大学 林学院,河北 保定 071001;2 .承德市园林局,河北 承德 067400;3. 河北省木兰围场国有林场管理局,河北 围场 068450)
北沟林场华北落叶松生物量模型的研究
姜 鹏1,董树国2,隋玉龙3,王骄洋1,王桂真1
(1. 河北农业大学 林学院,河北 保定 071001;2 .承德市园林局,河北 承德 067400;3. 河北省木兰围场国有林场管理局,河北 围场 068450)
本文以北沟林场华北落叶松为研究对象,利用统计学软件SPSS来拟合生物量模型,通过60株解析木的测量数据建立各器官的模型系统。模型系统共包括4部分,分别是:总量生物量模型、树干生物量模型、树枝生物量模型和树叶生物量模型。结果表明:建立的华北落叶松各器官生物量模型预估精度达到98%以上。筛选出总量及各部分生物量模型分别是:总生物量W总=-0.300+0.025D2H,树干生物量W干=-0.536+0.017D2H,树枝生物量W枝=0.054+0.006D2H,树叶生物量W叶=0.182+0.002D2H。各器官生物量残差的散点呈均匀分布,残差分布直方图分布近似正态,证明数学模型具有统计学上的意义。
华北落叶松;生物量;模型
森林生物量是生态学研究的基础工作之一,它也是生态学的重要的研究部分[1]。对生物量和生产力的调查和研究最早是上世纪60年代中期,是由国际生物学计划(IBP)中提出并开始的。而研究森林生物量最主要的方法就是建立生物量模型,同时也是一个比较准确的而有效的方式。林木生物量模型基本类型分为:线性模型、非线性模型、多项式模型3种类型,应用最为广泛和普遍且最具代表性的是非线生长性模型。以往都是以树木的实测数据为基础,对干、根、枝、叶、灌、草的生物量独立建模,这种建模设计合理,但是存在一个不相容的问题,即分量模型估计值之和与总生物量模型估计值不相等的问题,进而提出了比例平差法、直接控制法等[2-5]。生物量模型的成功建立,就可以用林木的易测因子(例如胸径、树高等)来推算出单株立木的生物量,而且可以在一定的判断系数(R2)范围是有效的、精确的,为单株立木的生物量的估算以及森林的生物量的估算提供依据和方便。本文以华北落叶松为研究对象,依托北沟林场为实验基地,对落叶松地上部分的生物量进行研究,做出多因子线性拟合模型。通过对落叶松生物量的基础数据的调查,并结合相关性分析和逐步回归方法,探讨了华北落叶松林的各器官生物量的分配规律,为建立落叶松和其它树种的非线性模型、多项式模型和各器官生物量值之和与全株生物量值相容性奠定基础。
1 研究地概况
研究地位于北沟林场内,林场坐标为北纬40°54′N,东经117°27′E,林场地处七老图岭山西侧,地势东北高,西南低;海拔800~1 600 m之间,色树梁东光顶是全场最高峰,海拔1 600 m;滦河支流——伊玛吐河由北向南从林区穿过,流入隆化境内。北沟林场为木兰林管局13个管辖单位之一,林场经营面积为5 667 hm2,有林地面积为5 000 hm2,占总面积的87.2%。该地区地处寒温带和中温带、半干旱和半湿润过渡的大陆季风气候区,冬季寒冷夏季凉爽,年均气温-1.4~4.7℃;无霜期短,每年无霜期为67~130 d;降雨主要集中在夏季的6~9月份,其年均降雨量390~570 mm之间。林场的土壤类型主要有棕壤、褐土、黑土、灰色森林土为主,和风沙土、草甸土和沼泽土这7类。森林以天然次生林和人工林为主,天然次生林白桦Betula platyphylla、柞树Quercus mongolica、五角枫Acer truncatum、榆树Ulmus spp.、山杨Pobulus davidiana等,人工林主要树种有油松Pinus tabulaeformis、华北落叶松Larix principis-rupprechti、云杉Picea asperata等。林区内生物资源十分丰富,有高等维管植物600多种,野生脊椎动物有20余种,鸟类有80余种。
2 研究方法
2.1 标准地设置及标准木的测定
根据北沟林厂的森林状况,选取落叶松林分生长状况良好且林型基本相同的落叶松纯林为试验设置标准地,选取10块r=20~30 m的圆形标准地,标准地面积为1 256~2 826 m2。以样地的中心为圆心,分别用支架罗盘测量角度,用皮尺测量每株树木到该圆心距离,极坐标为(α,x)。标准地的起测径阶为胸径大于等于5 cm的落叶松,对标准地内的每株落叶松逐株标号,并测量胸径(D)、树高(H)、枝下高、冠幅等测树因子。计算标准地内树木的平均胸径和平均树高,在标准地中找与平均胸径、平均树高接近并干形比较圆满通直的单株树作为解析木。每个标准地选6株标准木,均匀的分布在10个标准地内,共选60株落叶松伐倒,记录每棵树周围环境,并实测树高、胸径、和枝下高等。标准木以0.5 m为一个区分段,每段圆盘,室内测定树干解析的内业数据,测量各段树干鲜重和树枝、树叶鲜重,并按比例取样品烘至恒重,再计算出整株树的树干、树枝、树叶的干物质重量。样地标准木基本情况见表1。
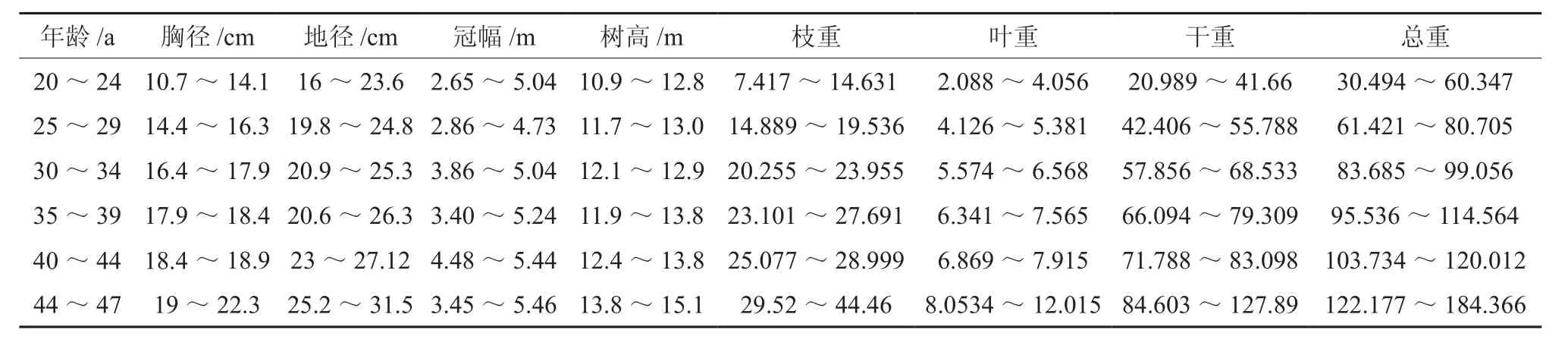
表1 标准木基本情况Table 1 General situation of standard trees
2.2 生物量的相关性和生物量建模及选择
标准木解析的数据处理和材积计算选取excel、SPSS[6]和Forstat[7](统计之林软件)进行处理。使用SPSS对标准木的胸径、地径、树高、枝下高和各个器官的生物量(总生物量量重total t、树干生物量量重trunk t、树枝生物量量重branch t和树叶生物量量重leaf t)进行相关性分析,分析实测数据和各个生物量之间的关系。
森林生物量的估算通过生物量模型。按照研究对象不同分为:单株生物量模型和大尺度森林生物量模型[4],本试验主要是对单株落叶松进行的研究。
同时运用SPSS和Forstat软件对华北落叶松的总生物量及各器官的生物量进行模型模拟分析,根据相关分析选取若干测树因子为预测变量,建立对预测变量与总生物量W总、树干生物量W干、树枝生物量W枝、树叶生物量W叶4者之间的生物量模型,生物量单位为kg。模型的优劣采用判断系数(R2)来进行评价和SPSS中逐步回归法,构建线性模型并进行精度比较,选出的数学模型对生物量的估算要有最好拟合度、最密切相关度,最适合的拟合模型。
3 结果与分析
3.1 标准木的相关性分析
标准木的相关性主要是对实测因子(胸径和树高等)和各器官的生物量(总重total t、树干重trunk t、树枝重branch t和树叶重leaf t)之间的相互关联性,选择Pearson相关系数,进行双尾检验(Two-tailed),结果见华北落叶松各器官和实测因子的相关性表2。
从表1可以看出,实测因子和各器官的生物量之间,各实测因子之间,各器官的生物量之间,在0.01的双尾检验都表现为显著正相关。胸径与各器官的生物量相关系数明显都大于0.94,由此可以说明在显著水平为0.01的条件下,胸径与各器官的生物量之间存在很强正相关关系。其次是树高与各器官的生物量相关系数比较明显,都大于0.89,地径与器官的生物量相关系数都大于0.86,树高和地径与各器官的生物量也表现了较强的正相关关系。枝下高与器官的生物量相关系数小于0.8,说明在显著水平为0.01的条件下,枝下高与各器官生物量的正相关关系一般。当相关系数绝对值大于0.8时,说明两个变量之间有较强的线性关系,相关系数数值越大表现的相关性越密切,使用该因子拟合出来的模型,模型精度高。故选择胸径和树高两个因子作为拟合因子。
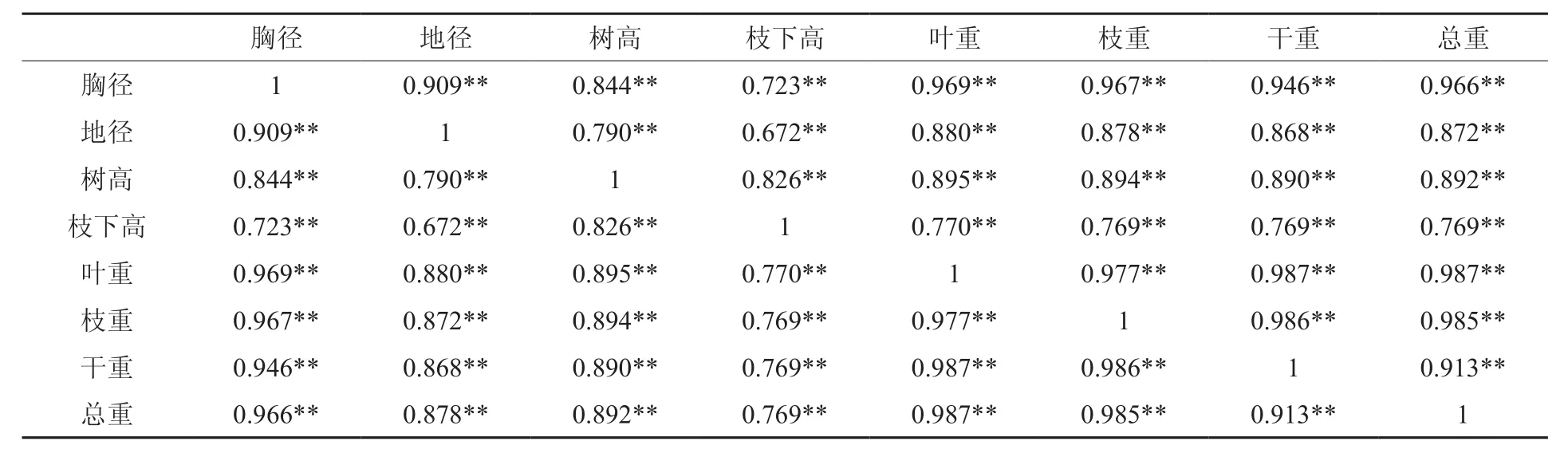
表2 华北落叶松各器官和实测因子相关性Table 2 Correlation between organs and measured factors of Larix principis-rupprechti
3.2 模拟建模与模型分析
考虑到自变量的选择重要性,并根据相关性的分析选取胸径(D)和树高(H)作为自变量,又因为胸径和树高的相关系数为0.844,两者之间表现出很强的相关性,所以添加自变量胸径平方(D2)和胸径平方与树高的积(D2H)。由于各器官生物量与各变量都存在一定的相关性,所选取D、D2、H、D2H这4个自变量分别与各器官生物量有较强的相关性,变量对模型的影响很强,从而可以提高模型的精度。
以各器官生物量和总生物量做为因变量,运用SPSS中的逐步回归法和Forstat软件中的通常线性回归,选用强迫引入法(Enter),使每个自变量一次性进入回归模型,建立实测数据与各生物量之间的一一对映的器官生物量线性模型。根据R2值筛选去掉一些R2值小的数学模型,筛选结果见华北落叶松林木生物量回归数学模型表3。
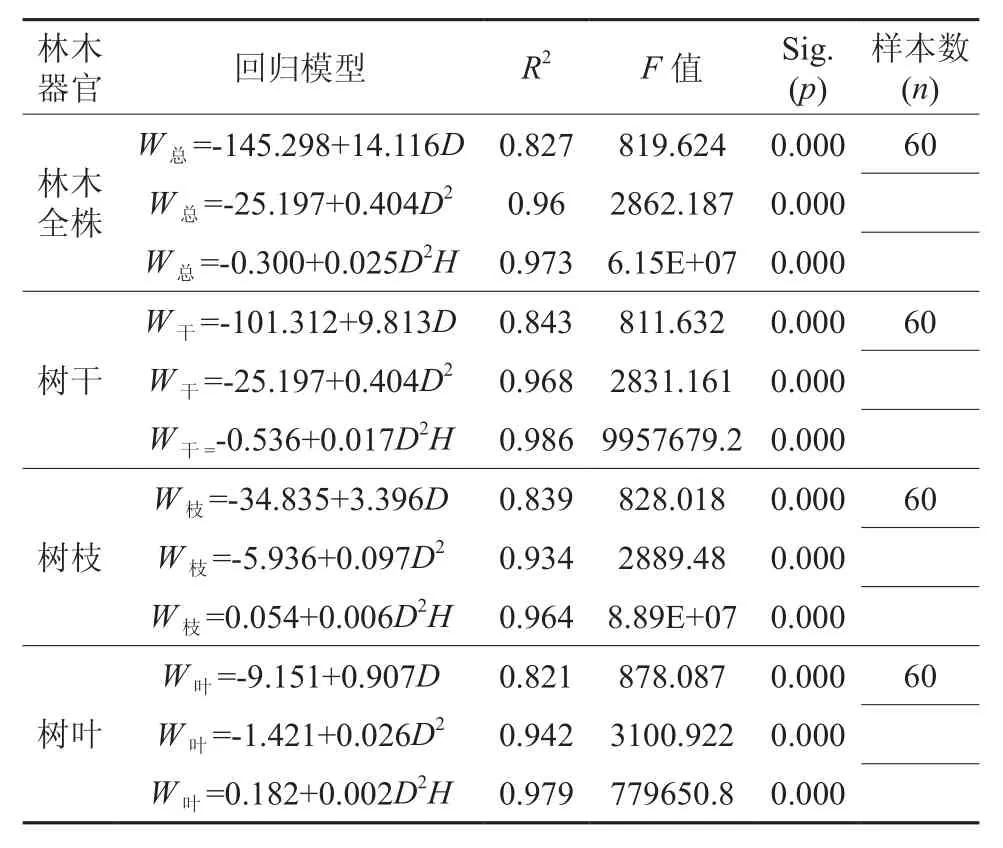
表3 华北落叶松林木生物量回归模型Table 3 Regression models of Larix principis-rupprechti whole-plant biomass and organs biomass
表3显示了,D、D2、D2H这3个变量与落叶松各生物量的拟合数学模型,和较高的数学模型拟合系数。全株生物量模型的R2分别为0. 827、0. 96和0.973,树干生物量模型的R2分别为0.843、0.968和0.986,树枝生物量模型的R2分别为0.839、0.934和0.964,树叶生物量模型的R2分别为0.821、0.942和0.979,四种模型里都是自变量为D2H的因子拟合最好。从表中可以看出所有的数学模型都是一元线性模型,所有的生物量模型的R2值都大于0.8,表现出较高的相关性,且各生物量模型拟合变量D2H较D和D2所拟合生物量模型的拟合相关系数高,表明该变量是一个比较理想的回归变量。
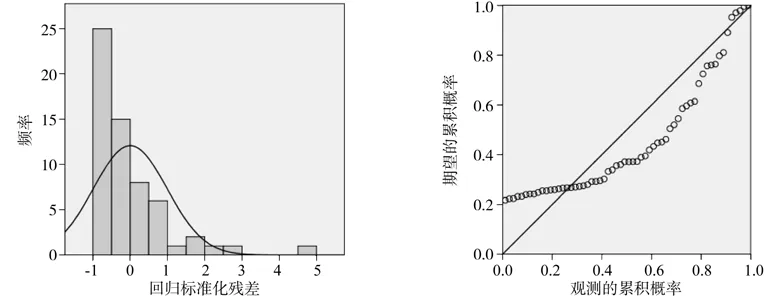
图1 落叶松全生物量的直方和P-P图像Fig.1 Histogram and normal probability of Larix principis-rupprechti whole-plant biomass
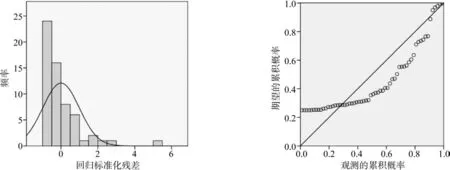
图2 落叶松树干生物量的直方和P-P图像Fig.2 The histogram and normal probality plot of Larix principis-rupprechti trunk biomass
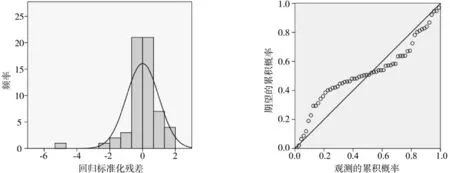
图3 落叶松树枝生物量的直方和P-P图像Fig.3 Histogram and normal probability of Larix principis-rupprechti branch biomass
3.3 标准化残差的检验
根据预测值和实际样本值之间的关系进行残差分析,分别做出华北落叶松各生物量标准化残差的直方图(Histogram)和标准化残差的正态概率图(Normal probality plot,P-P图),对地上部分的全株、干、枝和叶残差分析图分别见图1、2、3、4。
由图1的直方图可以看出,残差比较符合正态分布,正态分布的负偏差的频率大于正偏差,分布整体略微向负偏差倾斜,但也存在这一个非常大的正偏差。而正态P-P图显示出标准化的残差散点基本分布在直线两侧或直线上,线下分布较多,最大偏差出现在(0.0,0.21)左右,整体没有出现发散现象。
图2的直方图和图1的直方图表现类似,正态P-P图稍有区别,个别点距离直线较远,最大偏差出现在(0.0,0.22)左右,不存在整体发散现象。
图3直方图的残差基本符合正态分布,正态分布的正负偏差的频率相差不大,但图中存在着一个非常大的负偏差。其正态P-P图显示出标准化的残差散点比较紧密的分布在直线两侧或直线上,直线的两侧分别差别不大,大约在(0.2,0.4)出现最大偏差,残差散点比较均匀。
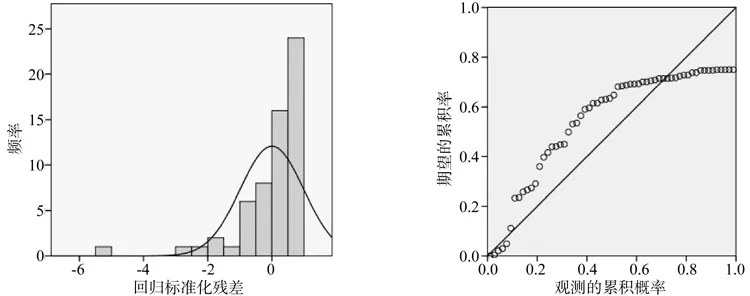
图4 落叶松树叶生物量的直方和P-P图像Fig.4 Histogram and normal probability of Larix principis-rupprechti leaf biomass
树叶的生物量直方图(见图4)可以看出,残差基本符合正态分布,与树干的生物量直方图分布大体相反,正态分布的负偏差的频率小于正偏差,分布整体略向正偏差倾斜,同样存在着一个非常大的负偏差。树叶的正态P-P图也与树干的正态P-P图直线方向上相反,残差散点大体分布在直线两侧或直线上,线上散点分布多余线下,最大偏差出现在(1.0,0.77)左右,整体没有出现发散现象。
综上所述,全株和树干生物量各器官生物量残差的散点分布极为相似,这也符合了树干生物量是全生物量的主要组成部分,占总生物量的50%~70%。图1~图4的各器官生物量残差的分布近似正态分布,出现小部分的正或负偏差和个别的大偏差,在正态P-P图的残差散点分布较均匀,线的单侧散点分布较多,没有发生发散现象,或者出现散点的异常值现象,相关性和残差分析表明对生物量模型的估计良好。
4 结 论
通过对北沟林场的华北落叶松生物量模型的建立与评价,最优模型为:树干生物量W干=-0.536+0.017D2H,树枝生物量W枝=0.054+0.006D2H,树叶生物量W叶=0.182+0.002D2H,总生物量W总=-0.300+0.025D2H。落叶松的生物量残差频率的分布近似正态分布,残差散点在正态P-P图呈现均匀分布,线的单侧散点分布较多,没有出现发散现象或者散点的异常值,相关性和残差分析证明生物量模型是可靠的。
[1] 孙玉军,张 俊,韩爱惠,等.兴安落叶松幼中龄林的生物量与碳汇功能[ J].生态学报,2007,27(5): 1756 -1762.
[2] 张世利,刘 健,余坤勇.基于SPSS相容性林分生物量非线性模型研究[J].福建农林大学学报:自然科学版, 2008, 37(5):496-500.
[3] 多立安,田德昌,崔艳丽,等.羊草十杂类草草原地上生物量增长动态的研究[J].东北农业大学学报, 1995,26(3):297-301.
[4] 吴亚坤,周连仁,郭百雷.肇州县盐渍土生物修复对草地生物量的影响[J].东北农业大学学报, 2006, 37(1): 37-42.
[5] 程堂仁,冯 菁,马钦彦,等.小陇山油松林乔木层生物量相容性线性模型[J].生态学杂志, 2008, 27(3): 317-322.
[6] 洪 楠. SPSS for Windows统计分析教程[M].北京:电子工业出版社, 2000.
[7] 唐守正,郎奎建,李海奎.统计和生物数学模型计算[M].北京:科学出版社, 2008: 291-293.
[8] 王维枫,王雪峰,赵浩彦.森林生物量模型综述[J].西北林学院学报,2008, 23(2): 58.
[9] 张浩军,刘华星,王懿祥.森林生物量相对生长方程的比较选择[J].中南林业调查规划, 1997,16(3): 58-60.
[10] 曾伟生,肖前辉,胡 觉,等.中国南方马尾松立木生物量模型研建[J].中南林业科技大学学报, 2010, 30(5): 50-56.
[11] 李 宏,唐守正.林业产业结构研究综述[J].世界林业研究,2000, 13(2): 41-46.
[12] 曾慧卿,刘琪璟,马泽清,等.千烟州灌木生物量模型研究[J].浙江林业科技, 2006, (26): 14-16.
Study on biomass model of Larix principis-rupprechtii in Beigou forest farm
JIANG Peng1, DONG Shu-guo2, SUI Yu-long3, WANG Jiao-yang1,WANG Gui-zhen1
(1. College of Forestry, Agricultural University of Hebei, Baoding 071000, Hebei, China; 2. Chengde Gardening Bureau, Chengde,067400, Hebei, China; 3. Hebei Administration of Mulanweichang National-owned Forest Farms, Weichang 068450, Hebei, China)
By taking the North China larch in Beigou Forest Farm as the research object, and using statistical software SPSS, the biomass models were fi tted. Based on the metrical data of 60 strains analytic trees, a model system for the organs was setup. The model system consists of four parts, namely: total biomass model, stem biomass model, twigs biomass model and leaves biomass model. The results show that the established larch organ biomass models’ predictive relative accuracies were all over 98%. Eventually, the total amount and biomass model were fi ltered as followings: total biomass Wtotal=-0.300+0.025D2H, trunk biomass Wtrunk=-0.536+0.017D2H, branches biomass Wbranch=0.054+0.006D2H, leaf biomass Wleaf=0.182+0.002D2. The biomass of residuals scatter evenly distributed, residual distribution histogram distribution was approximately normal, thus proving that the mathematical model has statistically meaningful.
Larix principis-rupprechtii; biomass; model
S718.55+6
A
1673-923X(2013)07-0131-05
2012-10-16
“三北”地区水源涵养林体系构建技术研究与示范(2011BAD38B05)
姜 鹏(1984-),男,山东烟台人,硕士研究生,研究方向:森林可持续经营;E-mail:jiangpeng210@126.com
谷建才(1963-),男,河北藁城人,教授,研究方向:林业资产评估与管理
[本文编校:吴 毅]

