花园幽径句的自动分析算法评析
赵文文
(北京航空航天大学,北京 100191)
引言
语言中存在大量的歧义现象,以往对歧义的研究基本局限在永久歧义句,而对暂时歧义句注意得不够。由短暂歧义形成的花园幽径句(garden path sentence)是语言处理过程中一种特殊的局部歧义现象,具有很大的研究价值。目前国内花园幽径句的研究重点主要分为两方面:一方面是基于心理语言的分析,研究如何解读花园幽径句,焦点是消除歧义的机制和手段,即所谓析句策略 (parsing strategies)(蒋祖康2000;冯志伟2003a);另一方面是基于句法的分析,主要探讨该花园幽径句临时歧义的形成原因,一般是从语言结构本身进行探索,提出了“θ—挂靠原则”(θ-Attachment)等理论 (刘国辉,石锡书2005)。上述两类研究都取得了一定的成就,前者对于机器翻译、人工智能很有裨益,后者也在相当程度上揭示了花园幽径句的句法特征及其对歧义形成过程的影响。在当今社会高度智能高度信息化的大背景下,用计算机实现语言的自动分析显得尤为重要。本文将从自动分析算法入手,以实例分析评析花园幽径句的自动分析算法。
1.花园幽径句的定义
1970年,T.G.Bever在《语言结构的认知基础》(The Cognitive Basis for Linguistic Structures)一文中提出了英语中的一种特别的句子,即Garden Path Sentence。很典型的一个例子是“The horse raced past the barn fell”(跑过粮仓的马倒下了)。当读者读到“The horse raced past the barn”时,很自然的认为句子已经完整,raced一词是主要动词,在该句中做谓语,但是,当读者再往下读到fell的时候,才会恍然大悟,raced一词在句中并不做谓语,而是作为定语修饰horse,句中真正的谓语是出现在句末的fell。在理解此类句子时,读到句尾才会发现先前的理解是错误的,于是不得不返回句首对句子进行重新解读。冯志伟(2003a)将此类特别的句子形象的翻译为“花园幽径句”,将其定义为因语言的输入顺序导致句子组成成分之间的语法关系不确定而暂时引起歧义的一种特殊语言现象,并有一段很形象的描述,“我们在理解这个句子的时候,正如我们走进一个风景如画的花园,要寻找这个花园的出口,大多数人都认为出口一定应该在花园的主要路径的末端,因此可以信步沿着主要路径自然而然地、悠然自得地走向花园的出口,正当我们沿着花园中的主要路径欣赏花园中的美景而心旷神怡的时候,突然发现这条主要路径是错的,它并不通向花园的出口,而能够通向花园出口的正确的路径,却是在主要路径旁边的另一条被几乎游人遗忘的毫不起眼的荒僻的幽径。”当然,花园幽径句不只存在于英语当中,而是广泛存在于各种语言当中。如在汉语中,“他一读书就掉了”,在读到“读书”时,读者会很自然的将“读”作为动词,“读书”结合在一起来理解全句,但后来发现其实正确的理解应该是将“读”和“书”分开,“书”是后面的动词“掉”的主语(曲涛,王准宁2005)。
花园幽径句有三个句法语义特征:1)花园幽径句是临时的歧义句,句子的前段有歧义,但是整个句子没有歧义;2)人们在理解花园幽径句的前面的歧义段的过程中,不同的歧义结果之间有优先性,有的歧义解释是人们所乐于接受的,有的歧义解释是人们不太愿意接受的;3)人们不愿意接受的解释其实这个句子正确的分析结果(冯志伟2000)。
2.基于短语结构语法的花园幽径句自动句法分析
工程主义取向的计算语言学家认为从研究程序上讲,计算语言学研究一般分为三个阶段:1)数学建模。计算机无法像人类一样认知自然语言,因此在对自然语言进行处理的时候需要把自然语言形式化,使之能以一定的数学形式严密而规整的标示出来,即为有关的语言问题建立数学模型,因此需要选择恰当的形式语法(formal grammar)使得自然语言中的句子结构用某种数学形式明确而清晰地表达出来;2)算法设计。为了能让计算机根据语法规则自动分析自然语言,必须要为自然语言设计相应的算法。此阶段要将严密而规整的数学形式以算法的形式表达出来,所以需要研究句子分析的严格的手续(procedures)并抽象成机械而明确的步骤,一步步逼近分析结果;3)程序实现。根据算法用程序语言编写计算机程序,使之在计算机上得以实现(computer implementation)(袁毓林 2001)。
计算语言学分析自然语言的方法主要有两种:一种是基于规则的方法,一种是基于统计的方法。实践证明,这两种方法各有千秋。尽管基于统计的方法对于大规模真实文本的处理比较适合,但基于规则的方法的作用也不容小觑,而基于短语结构语法的自动句法分析方法,就是基于规则的方法的一个重要方面 (冯志伟2003b)。
乔姆斯基的形式语法G是一个四元组
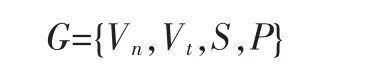
其中,Vn是非终极(non-terminal)词汇集,Vt是终极(terminal)词汇集,S 表示初始符号(starting point),P 表示重写规则 (rewrite rules)。P所表示的重写规则是上下文无关的,该种语法是一种上下文无关语法(context-free grammar,CFG)也叫做上下文无关的短语结构语法(context-free phrase structure grammar),或者叫做短语结构语法(phrase structure grammar,简称PSG)。
冯志伟(2000)介绍了5种主要的基于短语结构语法的自动句法分析方法,即自顶向下分析法、自底向上分析法、富田算法、左脚分析法以及CYK算法。我们通过自顶向下分析法以及自底向上分析法对花园幽径句进行分析,以Pritchett(1988)中的典型花园幽径句为例:

2.1 自顶向下分析法(top-down parsing method)
自顶向下分析法是指在分析句子时,根据重写规则,从初始符号开始,自顶向下的进行搜索,构造推导树,一直分析到句子结尾为止。在搜索过程中,搜索目标首先是初始符号S,从S开始,计算机选择文法中使用的规则来替换搜索目标,并用文法规则右边部分同句子中的单词相匹配,如果匹配成功,则抹去这个单词,在搜索目标中记录有关规则,然后继续对输入句子中的遗留部分进行搜索,如果分析到句子的结尾,搜索目标为空,则分析成功。如果再搜索过程中,搜索目标为空但句子中仍有部分遗留,就会发生回溯(backtracking),在有遗留部分的步骤中改用规则,从而使搜索得以成功。
对于例(1),我们提出以下文法:

根据以上文法,例(1)的分析过程如下(向下的箭头“↓”旁边注明规则的号码):

如果根据规则(9)抹去river,句子中还有遗留部分sank,而这时搜索目标已经变空,分析无法继续进行下去,因而发生回溯,回溯到第(2)步,看一看是否还能利用别的规则进行分析:

在第一次分析过程中,由于使用了规则(2),使得后面的分析无法继续,所以发生了回溯(backtracking),在第(2)步不再使用规则(2)而改为使用规则(3),从而使搜索得以成功。
根据这样的搜索过程,我们可以把例(1)两次分析的推导树表示如图1中的(a)(b)所示:
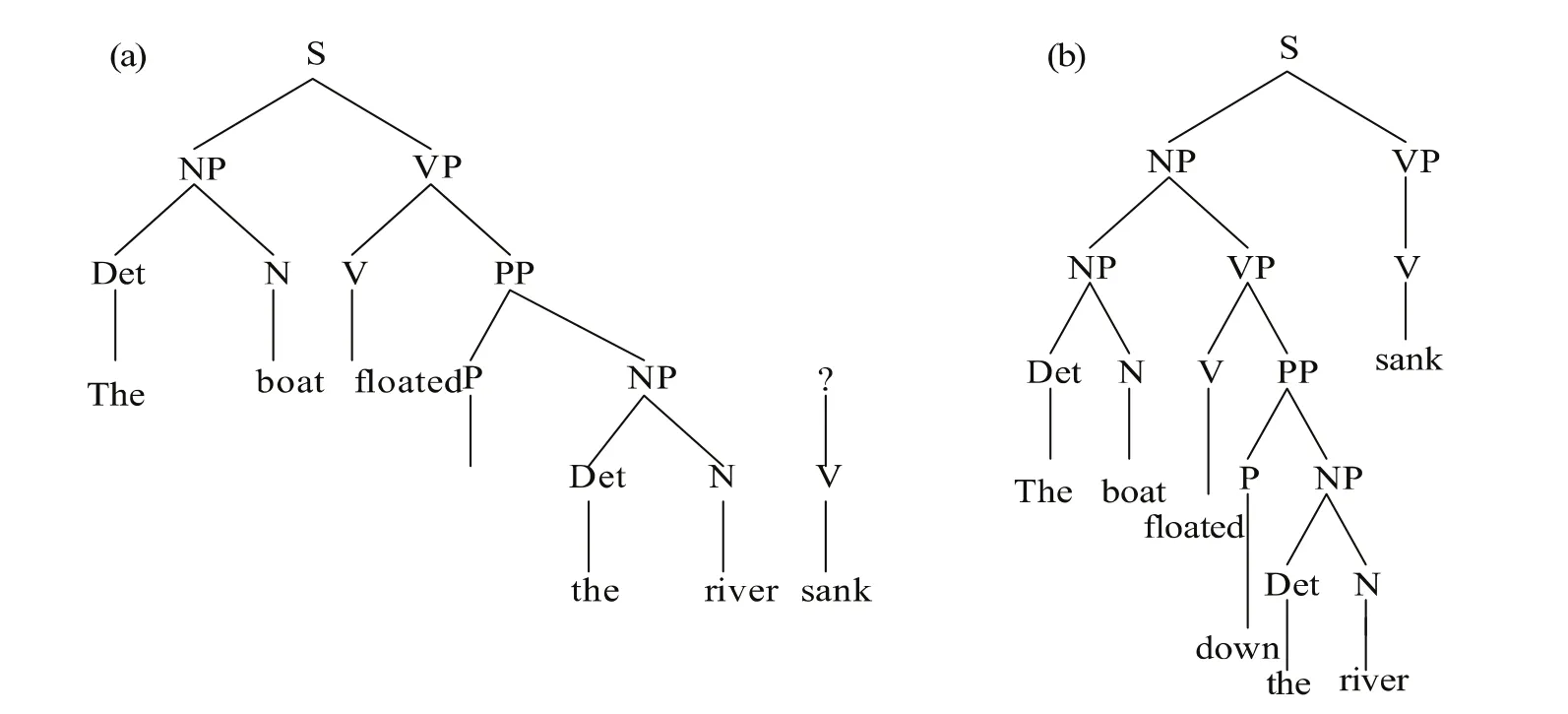
图1 自顶向下分析法推导树
2.2 自底向上分析法(bottom-top parsing method)
自底向上分析法是指从输入句子的句首开始顺次取词向前移进(shift)并根据文法的重写逐级向上归约(reduce),直到构造出表示句子结构的整个推导树为止。它实际上是一种 “移进一归约算法”(shift-reduce algorithm),它对句子中的单词取词是顺次“移进”,而在利用文法中的重写规则时是按条件“归约”。
这种算法利用一个栈来存放分析过程中的有关已经走过的过程的信息,并且根据这种信息和当前正在处理的符号串来决定究竟是移进还是归约。所谓“移进”,就是把一个尚未处理过的符号移入栈顶,并等待更多的信息到来之后再做决定;所谓“归约”。就是把栈顶部分的一些符号,由文法的某个重写规则的左边的符号来替代。这时,这个重写规则的右边部分必须与栈顶的那些符号相匹配。用这样的办法对栈中的符号以及输入符号串进行移进和归约两种操作,直到输入的符号串处理完毕并且栈中仅剩下初始符号S的时候,就认为输入符号串被接受。如果在当前状态,既无法进行移进,也无法进行归约,并且栈并非只有唯一的初始符号S,或者输入符号串中还有符号未处理完毕,那么,输入符号串就被拒绝。在分析过程中,有时既可以进行移进操作,又可以进行归约操作,这种情况,称之为“移进一归约冲突”,简称“移归冲突”;有时会有多个规则都能满足归约条件,这种情况称之为“归约一归约冲突”,简称“归归冲突”。什么时候进行移进操作,什么时候进行归约操作,怎样定义归约的条件,这些问题是移进—归约算法的中心问题(冯志伟,2000)。
以例(1)以及上文中提出的文法为例,自底向上分析法的分析过程如下:

这时,文法中不再有合适的规则,分析无法继续进行,于是返回到第(17)步,先不采用规则(4)规约,而是移进下一个单词sank,然后采用规则(11)进行规约,分析如下:
这时,栈中最终只剩下初始符号S,因此该句被接受,分析成功,分析推导树如图2所示。
根据以上算法分析可以看出,常用的自顶向下分析法以及自底向上分析法在分析花园幽径句是都需要回溯。回溯会影响分析算法的效率。为了避免回溯,提高自动分析算法的效率,冯志伟(2003b)指出,由美国计算机学者J.Earley提出的Earley算法可以有效的避免回溯,而该种算法,是用来分析花园幽径句最优最高效的算法。


图2 自底向上分析法推导树
3.无需回溯的Earley算法
依尔利算法的核心是线图(chart)。在表示语言信息方面,线图比树形图更为优越。在线图中,对于输入句子中每一个词,都可以用一个状态表来表示分析进程对于这个词所达到的位置。在句子分析结束时,线图可以把所有可能的分析结果都精练地表示出来。线图中的状态包括三方面的信息:关于与语法中的某一规则相对应的子树(sub-tree)的信息;关于在这个子树的分析进程中已经完成了的分析结果的信息;关于这个子树当前所处位置与输入句子中相应的位置的信息。这些信息采用点规则(dotted rule)来表示。所谓点规则,就是加了点的上下文无关文法的规则,它与一般的上下文无关文法规则的不同之处就在于规则中加了点,用这个点来表示这个上下文无关规则在分析进程中所处的状态。除了在上下文无关文法的规则中加点之外,在点规则中,还用两个数字来表示相应状态开始的位置和这个点在当前所处的位置。线图是一个非成圈的有向图(Directed Acyclic Graph,简称 DAG)。 Earley 算法有三种不同的基本操作,包括 Predictor(预示),Scanner(扫描),Completer(完成)。文章篇幅有限,本文在此不对Earley算法及其线图表示做详细介绍,只对花园幽径句的线图做一介绍。
对于例(1),我们提出如下文法:

根据Earley算法对其进行分析,分析结构可用线图表示,如图3所示。
在上述分析过程中,在(0,3)之间和(0,6)之间,曾经两次规约为句子S,但是,由于花园幽径句的长度为7,两次规约都以失败告终,只有在(0,7)之间时,分析成功。在(0,6)这一段,弧上的规则有歧义,而当分析完(0,7)时,弧上的规则只有一个,即SNP VP.,整个句子的结构并不存在歧义,而花园幽径句正式这样,属于潜在歧义句,整个句子在读到末尾时并无歧义,这种算法符合花园幽径句的特点。如上我们可以看出,Earley算法的整个分析步骤清晰而紧凑,并未产生回溯,可以大大提高自然语言的分析效率,因此,冯志伟(2003b)建议采用Earley算法来分析花园幽径句。
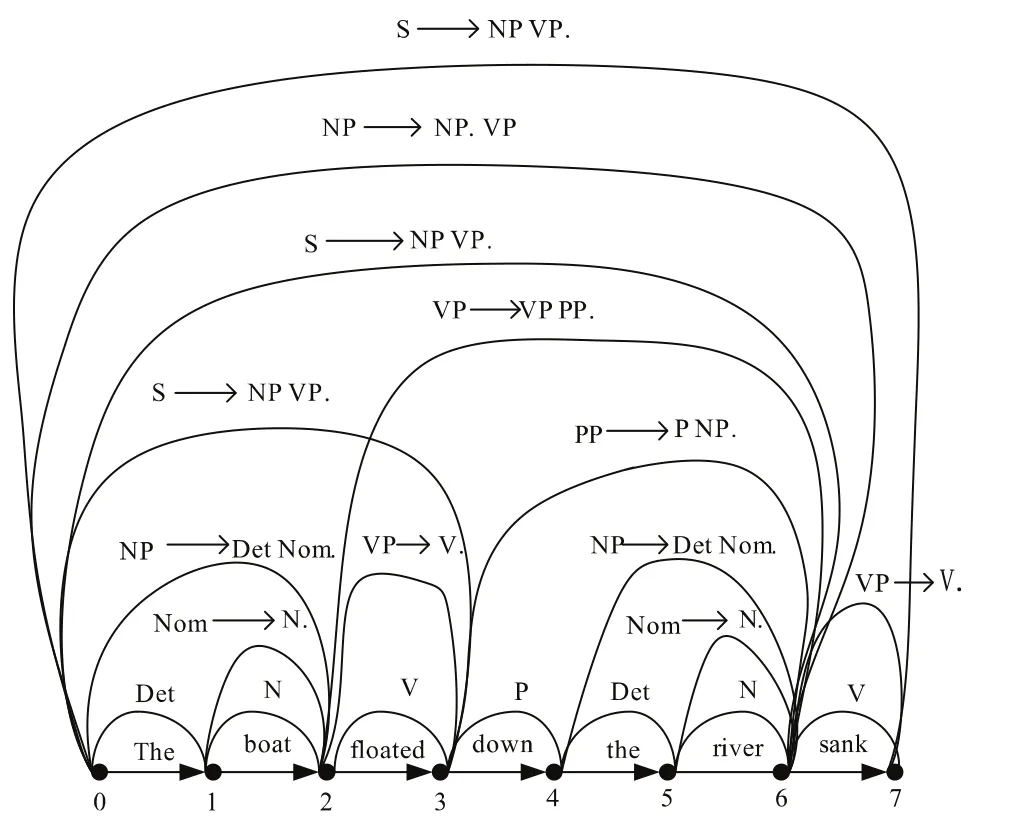
图3 Earley算法分析结果的DAG表示
结语
花园幽径现象具有层级存在性、理解折返性、认识顺序性和纠错控制性(杜家利,于屏方2011),而这体现在机器处理当中,便是自动分析算法中的回溯现象。在自然语言中,有短暂歧义形成的花园幽径句是一种很有研究价值的歧义现象,因为它涉及句法,语义和语用多个方面。计算机语言涉及到自然语言的形式化,在该种上下文无关语法当中,花园幽径句的自动分析也很值得研究,因为很多算法对它的分析都涉及到回溯,无法进行高效的分析。但Earley算法作为一种无回溯的自动分析算法,是自动分析花园幽径句的最优算法。本文只讨论了语言自动分析算法中常用的两种算法,自顶向下分析法以及自底向上分析法对英语中花园幽径句的解析,同时也用冯志伟(2003)指出的花园幽径句的最优算法——Earley算法对其进行了解析,但并未涉及汉语花园幽径句的算法分析,还需进一步深入自动分析算法在汉语花园幽径句中的运用。
Bever T.G.(1970).The Cognitive basis for linguistic structures[A].In J.R.Hayes,Cognition and Development of Language.New York:Wiley.
Pritchett,B.L.(1988).Garden Path Phenomena and the Grammatical Basis of Language Processing[J].Language(64).Linguistic Society of America.
杜家利,于屏方 (2011).花园幽径现象认知解读的程序化特性分析 [J].计算机工程与应用47(21)。
冯志伟 (2000).基于短语结构语法的自动句法分析方法 [J].当代语言学 (2)。
冯志伟 (2003a).花园幽径句的自动分析算法 [J].当代语言学 (4)。
冯志伟 (2003b).一种无回溯的自然语言分析算法 [J].语言文字应用 (1)。
蒋祖康 (2000).“花园路径现象”研究综述 [J].外语教学与研究 (4)。
刘国辉,石锡书 (2005).花园幽径句的特殊思维激活图式浅析[J].外语学刊 (5)。
曲涛,王准宁 (2006).浅谈花园幽径现象 [J].吉林教育学院学报 (8)。
袁毓林 (2001).计算语言学的理论方法和研究取向 [J].中国社会科学(4)。

