摩擦换向抽油系统中摆线针轮的可靠性优化

陆 荣，张兴福，张艳凤

（沈阳农业大学 高等职业技术学院，辽宁 沈阳 110122）

0 引言

在摩擦换向抽油机中，减速器由电机正反向驱动使摩擦轮做换向转动，带动光杆上下运动使抽油泵实现抽油。其中摆线针轮减速器是重要的传动机构，摆线针轮作为关键部件直接影响着系统的可靠性。常规优化设计是把设计变量处理为确定的变量，未考虑可靠性因素建立常规数学模型［1］，难以反映真实工况；而可靠性设计是把相关设计变量处理为随机变量，根据可靠性设计准则建立概率数学模型，未考虑优化方法，则对于某些设计问题也不能给出理想的结果［2，3］。本文结合可靠性理论和优化设计，选取可靠度为约束函数，对摆线针轮建立可靠性优化数学模型，并根据实例进行优化求解。

1 建立数学模型

可靠性优化设计即把机械零部件的可靠度要求结合在优化问题的约束内，或者结合到优化问题的目标函数中，运用优化方法得出参数的最优解［4］。在实际生产中可预先给定可靠性指标，以可靠度作为约束条件，使其他指标（成本、重量、体积）达到最优［5］。

1.1 确定目标函数及设计变量

强度理论表明，对于一定的材料选择合理的体积及参数可使零件的承载能力提高。负载不变的情况下，零件体积越小材料利用越充分；外廓尺寸一定时，应力越小承载能力越高。因此，以减速器的体积为摆线针轮行星减速器设计的目标函数，在满足给定要求的前提下寻求最小值。摆线轮体积［6］可以表示为：

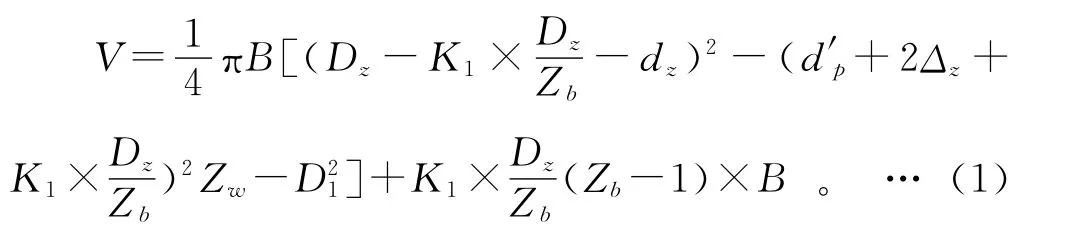
其中：B 为摆轮宽度；Dz为针轮分布圆直径；K1为短幅系数；dz为针 齿 套 外 径；D1为 转 臂 轴承外径；d′p为柱销直径；Zb为针轮齿数；Zw为柱销数目；Δz为柱销套壁厚。

独立 设计变 量确定为：X＝［Dz，B，K1，dz，D1，d′p］T＝［x1，x2，x3，x4，x5，x6］T。

将设计变量代入式（1），则目标函数为：

1.2 选取约束条件

（1）短幅系数约束条件为：

（2）摆线轮宽度限制条件为：

（3）摆线齿廓不根切条件为：

其中：αmin为理论齿廓最小曲率半径系数。

（4）柱销孔最大直径限制条件为：

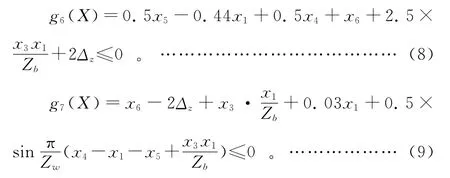
（5）针轮分布圆直径限制条件为：

其中：Mv为输出轴阻力矩。

（6）建立强度可靠性约束条件，以应力及强度为随机变量，设其服从对数正态分布［7］，根据可靠性理论，强度可靠性系数方程为：

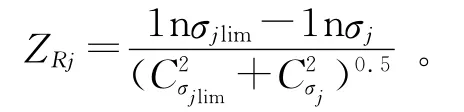
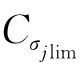
Rj＝φ（ZRj）

其中：φ（·）为标准正态分布函数。

可靠性约束条件为：

其中：［Rj］为摆线针轮齿面强度可靠度。

由此可建立一个单目标函数的数学模型，即包括6个设计变量及10个约束条件的非线性规划：

minf（X） X∈R6

s.t gi（X）≤0 i＝1，2，…，10 。

2 优化求解

利用MATLAB优化工具箱进行可靠性优化的编程求解［8］。可靠性优化程序框图见图1。

3 实例分析

摩擦换向抽油系统中，摆线针轮行星减速系统功率P＝30kW，转速n＝1 000r／min，传动比i＝71，工作时间为每天8h，工作平稳。

优化设计中利用SQP 算法，经过4次迭代，目标函数计算39次，海赛矩阵修改5次，最终优化满足终止条件，搜索方向小于两倍options.TolX，最大违约值小于options.TolCon，计算机停止迭代计算。

图1 可靠性优化程序框图

对计算机迭代计算的最优值进行圆整，将得到优化设计的结果与原设计的结果比较，见表1。从表1中可以看出，每天工作8h，在工作平稳的情况下，当主要元件工作可靠度为0.98 时，摆线轮的体积减少11.33%；可靠性优化结果圆整后的数据并未使得摆线针轮的体积发生大幅改变，与原设计结果比较，体积约减少11.13%。

表1 齿摆线针轮优化设计结果对照表

4 结束语

本文以摩擦换向抽油机中行星减速器为研究对象，对减速系统中的摆线针轮进行了可靠性优化设计，建立了可靠性优化模型，并以实例进行设计分析。从优化结果可以看出，在满足可靠度的条件下通过优化减小体积10%以上，因而在保证其承载能力的前提下，无论是使用寿命及可靠性方面，还是减小结构尺寸、降低成本方面，可靠性优化设计方法对该传动的改善都优于常规设计方法，故该方法体现出明显的优越性，值得推广和进一步应用研究。

［1］ 符曦.系统最优化及控制［M］.北京：机械工业出版社，2004.

［2］ 陈立周.机械优化设计［M］.北京：冶金工业出版社，2005.

［3］ 谢里阳，王正.机械可靠性基本理论与方法［M］.北京：科学出版社，2009.

［4］ 刘金刚，王世鹏，解艳彩.广义随机空间内结构可靠性优化设计［J］.机械设计与研究，2010，26（5）：7－12.

［5］ 尹力.摆线针轮行星传动的可靠性优化设计［J］.重庆交通学院学报，2005，24（4）：149－151.

［6］ 阌帮春.机械设计手册［M］.北京：机械工业出版社，2010.

［7］ 吴迎学.摆线针轮行星减速器的模糊可靠性优化设计［J］.机械设计与制造，1998（4）：325.

［8］ 飞思科技产品研发中心.MATLAB6.5辅助优化计算与设计［M］.北京：电子工业出版社，2003.