模态分析技术在摩托车振动改进中的应用

魏喜明，白清祥，周昌林

（江门市大长江集团有限公司 研发中心，广东 江门 529030）

1 模态分析的定义和基本原理

1.1 模态分析的经典定义

将线性定常系统振动微分方程组中的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程，以便求出系统的模态参数。坐标变换的变换矩阵为模态矩阵，其每列为模态振型。模态分析的最终目标是识别系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。

1.2 模态分析的基本原理

首先考虑一下多自由度的动力学方程问题，设自由度数为n，则有：

其中：［M］、［C］、［K］分别为多自由度系统的质量矩阵、阻尼矩阵、刚度矩阵；｛x（t）｝、｛x·（t）｝、｛x··（t）｝分别为多自由度系统的位移向量、速度向量和加速度向量；｛f（t）｝为多自由度系统的受力向量。

然后对式（1）进行拉普拉斯变换，并且假定初始位移和初速度均为零，则得：

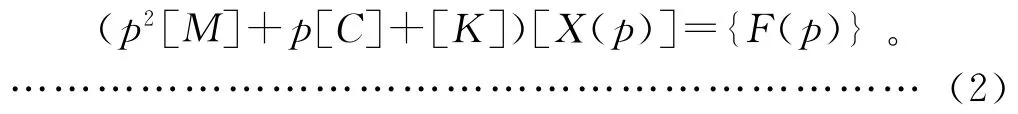
所以位移阻抗矩阵为：

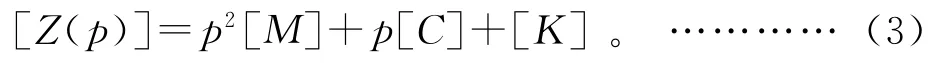
在多维度动力学问题中，传递函数用下式定义：

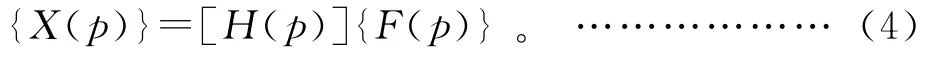
将式（4）对照式（2）、式（3）可得传递函数矩阵为：

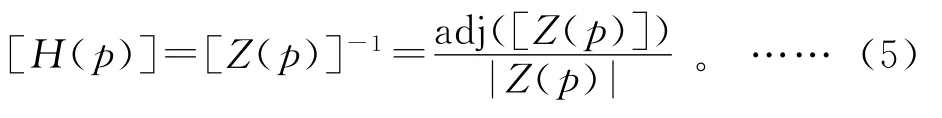
其中：adj（［Z（p）］）为［Z（p）］的伴随矩阵；｜Z（p）｜为［Z（p）］的行列式。显然，如果令：

则可以求得多个p 值，使得式（6）成立，而这些p 值就是系统极点，这些极点所对应的频率就是该系统的多种模态的固有频率。得到的多自由度系统模态的极点和共振频率参数如式（7）和式（8）所示：

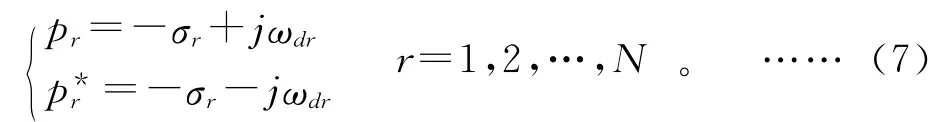
其中：pr和p＊r为多自由度系统的共轭极点；σr为模态阻尼衰减系数；ωdr为系统的有阻尼模态频率。ωdr的计算公式为：

其中：ωr为系统的无阻尼模态频率；ζr＝σr／ωr为模态阻尼比。

模态分析技术的主要任务是找出结构中问题模态的频率和振型，通过对模态频率和振型的理解进行有针对性的改进，从而达到改善振动或降低噪声的效果，本文通过国内某车的振动问题案例来进行具体说明。

2 模态分析技术在某摩托车振动问题改进中的应用

2.1 问题的提出及诊断

国内某摩托车在开发过程中，评价部门提出其左、右脚踏有共振问题，主要是在4 500r／min附近右脚踏共振，5 500r／min附近左脚踏共振。该振动将影响整车的舒适性，必须加以立项改进。笔者根据反馈描述对该车左、右脚踏的振动进行测试，结果如图1、图2所示。

从图1、图2可以看出左脚踏在5 580Hz附近、右脚踏在4 440Hz附近各有一个比较明显的振动放大，这是一个典型的共振问题。需分析该共振的主要共振频率，并对其模态特征进行调查。

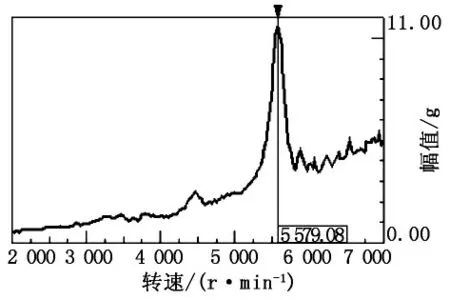
图1 左脚踏振动测试测试结果

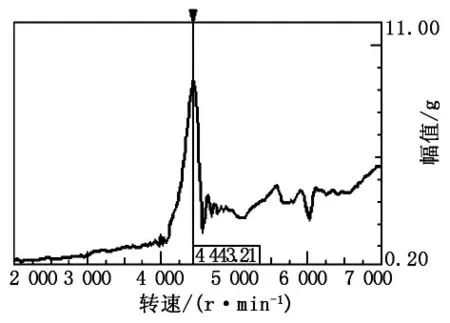
图2 右脚踏振动测试测试结果

2.2 频谱分析

对测得的数据进行阶次分析，分别如图3、图4所示。

图3 左脚踏频谱分析

图4 右脚踏频谱分析

由图3可知，左脚踏5 580r／min附近的共振模态是由发动机的2阶激励激发出来的，该模态的特征频率为186 Hz。由图4可知，右脚踏4 440r／min附近的共振模态也是由发动机的2阶激励激发出来的，该模态的特征频率为147Hz。

2.3 模态锤击实验验证

采用模态锤击法实验测试装配状态脚踏结构的共振频率，如图5所示。

通过锤击法模态实验找到了上述左、右脚踏的两个模态频率，印证了频率诊断中的模态的确存在。

图5 关于装配状态脚踏特征频率的模态实验

2.4 用CAE软件进行模态分析

边界条件：约束安装螺栓孔；网格类型：采用2阶Tetra单元；材料属性：采用橡胶和钢两种材料混合建模，分析结果如图6、图7所示。

图6 CAE模态分析一阶模态计算结果

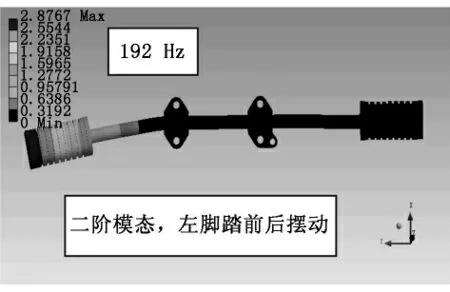
图7 CAE模态分析二阶模态计算结果

2.5 模态结果误差分析

对实验模态与计算模态结果进行误差分析，如表1所示。由表1可知，实验模态结果与CAE 计算模态结果非常接近，误差在2%左右，分析结果可靠，可以作为改进方案的依据。

表1 实验模态结果与计算模态结果误差分析

2.6 改进方案及其测试验证

根据上述CAE 模态计算结果对两只脚踏杆的前、后方向进行了有针对性的改进，改进后的振动测试结果如图8、图9所示。

采用改善方案后，评价部门进行了评价，认为改进方案的振动问题可以接受，该车振动问题得以解决。

3 总结

本文介绍了模态分析的基本原理，通过某摩托车开发中振动问题的解决流程阐述了其应用方法。在此案例中，采用了模态实验、振动信号频域诊断与CAE模态分析技术相结合的方法，解决了该车的左、右脚踏振动问题，为今后解决此类问题提供了新思路。

图8 左脚踏改进前、后振动对比

图9 右脚踏改进前、后振动对比

［1］ 庞剑，谌刚，何华.汽车噪声与振动：理论与应用［M］.北京：北京理工大学出版社，2006.

［2］ 马大猷.噪声与振动控制工程手册［M］.北京：机械工业出版社，2006.