基于改进粒子群优化LSSVM 的飞机发动机故障诊断
庄 夏,戴 敏,何元清
(1.中国民航飞行学院科研处,四川广汉 618307;2.中国民航飞行学院计算机学院,四川广汉,618307)
飞机发动机工作环境复杂、状态变化频繁,这使得飞机发动机的故障表现和故障征兆表现出多样性。及时地对飞机发动机进行故障检测和诊断,能有效地避免事故和由此带来的巨大损失[1]。
目前对飞机发动机进行故障诊断的主要方法主要有:基于气路参数的故障诊断方法[2]、基于融合技术的故障诊断方法[3]、基于Petri网的故障诊断方法[4-5]和基于人工智能的故障诊断方法[6-8]。这些方法都实现了飞机发动机的故障诊断,具有重要意义,但也存在着如泛化能力弱、需要大量样本数据等缺陷。支持向量机(support vector machine,SVM)[9]是在统计学理论的结构风险最小化的理论基础上发展而来,具有需要样本数据少、泛化能力强等优点,但其参数选取的好坏决定诊断性能。
因此,本文中提出一种基于粒子群算法(particle swarm optimization,PSO)[10]和支持向量机的故障诊断方法。实验表明,该方法能较为精确地实现飞机发动机故障诊断,具有很强的可行性。
1 LSSVM 故障诊断
1.1 LSSVM 故障诊断模型
最小二乘支持向量机(least squares support vector machine,LSSVM)[11]在经典SVM 的基础上,采用平方项作为损失函数,并采用等式约束代替不等式约束,从而将二次规划问题转换为线性问题进行求解,以提高训练速度。
LSSVM 的基本原理是通过非线性映射Ψ(x),将样本数据{xi,yi}从原空间映射到高维目标空间,在高维目标空间对未知函数采用下式进行估计:

式(1)中w 为超平面的法向量,θ为偏差。
LSSVM 将回归问题转换为具有最小结构风险的优化问题,如下式所示:
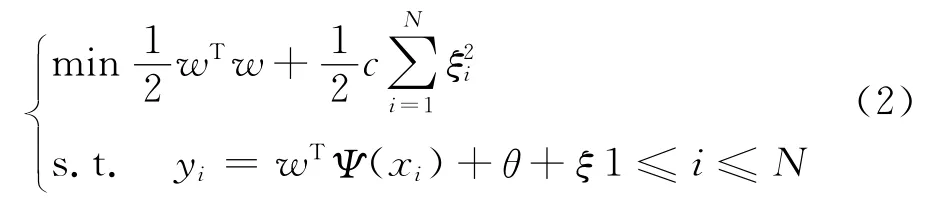
式(2)中c为正则化参数,ξi 表示第i个输出端误差,yi为输出实际值。为了对(2)进行求解,引入拉格朗日函数,消去约束,如下式所示:

式(3)中α 为拉格朗日算子。根据卡罗-库恩-塔克(karush-kuhn-tucker,KKT)条件,即:

利用式(4)对式(3)进行求解,可得式(5):

将上式消去w 和ξi,将式(2)所示的优化问题转换为下述线性方程:
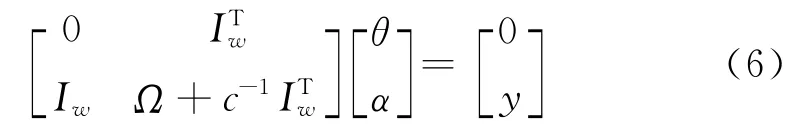
其中,Iw为对角元素为1 的对角矩阵;,Ω 为由元素Ωij组成的矩阵,Ωij=k(xi,xj),1≤i,j≤N,Ωij为LSSVM 中的核函数。
采用RBF径向基函数作为核函数k(xi,xj)=exp(-‖xi-xj‖/2σ2),σ 表示函数宽。将式(6)展开可得
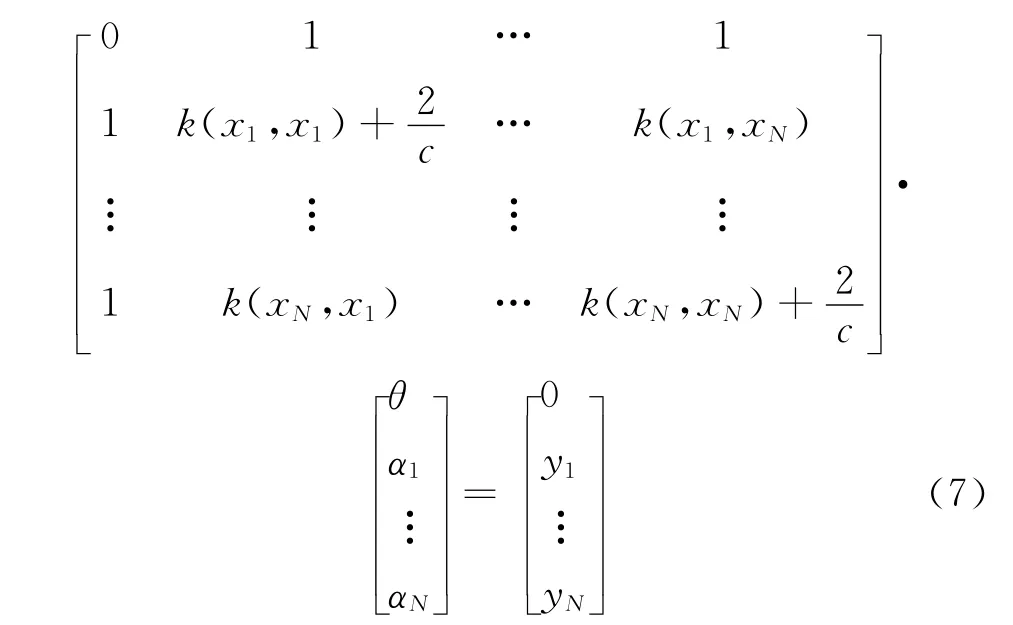
求解(7)可以获得分类决策函数:

1.2 多分类LSSVM 故障诊断原理
式(8)所示的决策函数输出为1或-1,仅能用于解决二分类问题,由于故障诊断通常是多分类问题,所以采用一对一算法,即先将训练集分为所有可能的类别组合,然后对每个类别组合分别使用一个LSSVM进行训练,分类需要构造n(n-1)个LSSVM,n 为故障种类数,最后通过对模型进行投票,将票数最多的定位最终的判别结果。
2 基于粒子群优化的故障诊断
2.1 经典粒子群算法
经典粒子群算法问题空间的每一个解表示为一个粒子。粒子具有2个特征,即位置和速度,位置可以表示为xi(t)={xi1,xi2,…,xiD},速度可以表示为vi(t)={vi1,vi2,…,viD},其中D 为维数。在每次迭代中,粒子均通过2个最优值,即个体最优值pdsti和全局最优值gbst对自身的位置和速度进行不断更新。位置和速度的更新公式为:

其中:c1和c2为学习因子,通常取值为1~2之间的随机数;λ1和λ2为(0,1)之间的随机数;ρ 被称为惯性权重。
2.2 改进的粒子群算法
对经典的粒子群算法进行改进,主要包含以下3个方面:
(1)设计自适应线性变化的惯性权重ρ,在搜索的初始阶段,使ρ取较大值,增强粒子的全局搜索能力,以保持解的多样性最大迭代;在搜索后期,为了让算法收敛,增加算法的局部寻优能力,使ρ取较小值,如下式所示:

其中,t表示当前迭代次数,tmax表示最大迭代次数。
(2)在算法后期最优解连续三代未发生变化时,引入小生境技术[12],以增强粒子的多样性。具体是通过引入排挤机制来实现,即通过产生若干粒子,以排挤种群中的一些相似个体。
(3)设计结合测试误差和训练误差的适应度函数,设e1为训练样本误差,e2为测试样本误差,则综合误差适应度函数Fit可以表示为
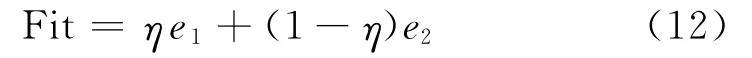
式中,η为侧重性系数。e1和e2由下式获得:
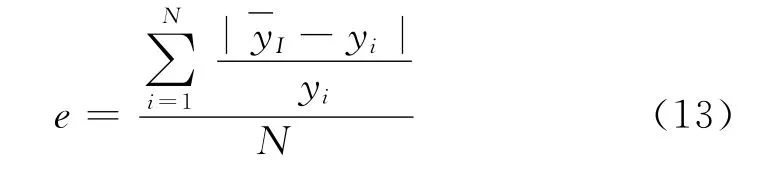
2.3 基于改进粒子群优化LSSVM 诊断算法
从式(8)可以看出,参数c和σ 对LSSVM 的分类性能具有较大影响,所以采用改进的粒子群算法对其进行优化,再采用具有优化参数的LSSVM 进行故障诊断。改进粒子群LSSVM 诊断算法如下:
初始化:学习因子c1、c2,惯性权重最大值ρmax、最小值ρmin,排挤因子CF,小生境半径r,最大迭代次数tmax。
步骤1:将粒子编码为二维向量(c,σ),并生成含有N 个粒子的初始粒子群,随机初始位置和速度。
步骤2:根据式(12)计算所有粒子的适应度并进行判断:当粒子的适应度Fit小于其个体历史最优适应度pbsti,则对pbsti进行更新;当粒子的适应度Fit小于所有粒子的历史最优适应度gbst,则对gbst进行更新。
步骤3:对粒子的历史最优适应度gbst进行判断,如果其值连续三代不发生变化,则引入小生境排挤操作,选择N/CF个粒子参与排挤运算,随机产生一批新粒子,计算新粒子与排挤成员之间的欧式距离d,当满足d≤r,采用新粒子代替排挤成员。
步骤4:根据式(9)和式(10)对粒子的速度vi(t)和位置xi(t)进行更新。
步骤5:迭代次数t=t+1;如果迭代次数t未达到最大值T 时,则转入步骤2继续迭代。
步骤6:采用上述步骤获得全局最优值gbst并用于初始化LSSVM,采用式(8)所示的决策函数构造n(n-1)/2个二分类器,实现故障诊断。
3 仿真实验
选取某型发动机的4个典型截面垂直和水平方向的8 个测点,即:风扇前支点水平和垂直振动速度,分别记为v1和v2;中介机匣水平和垂直振动速度,分别记为v3和v4;低压涡轮支点水平和垂直振动速度,分别记为v5和v6;;外置附件机匣水平和垂直振动加速度,分别记为v7和v8。故障征兆为4种:转子不对中、动不平衡、支撑刚度过大和无故障,因此输入数据维数为8,输出值范围为{1,2,3,4},样本数据共16组,其中8组作为训练数据,剩下8组作为测试数据。训练数据见表1。
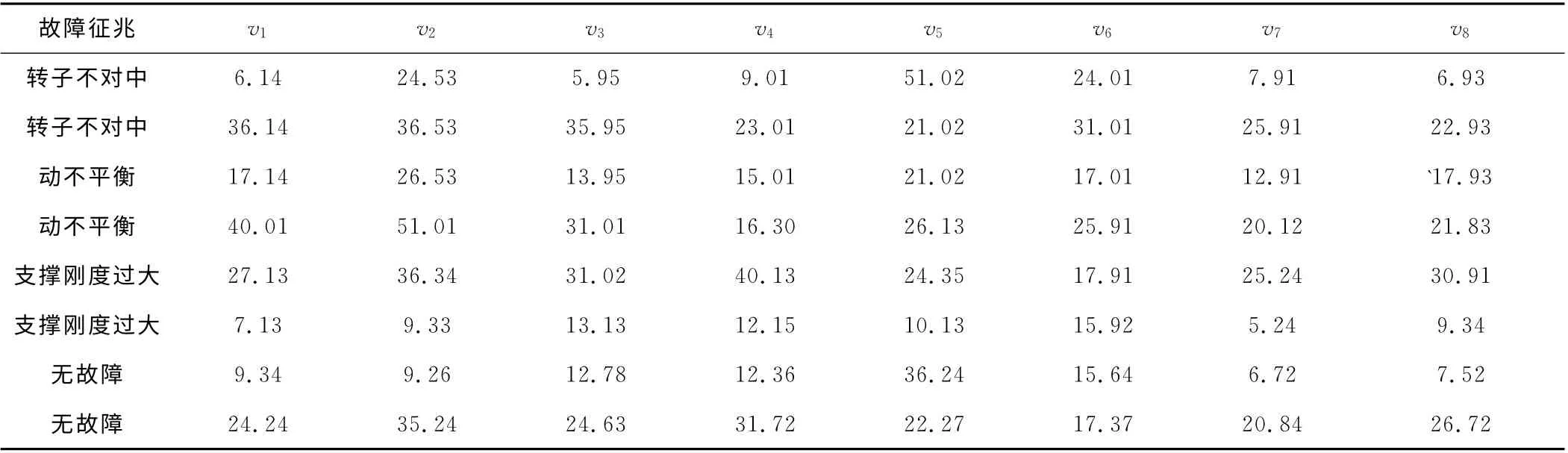
表1 某飞机发动机故障诊断样本数据mm/s-1
采用上述算法进行故障诊断,参数设置如下:粒子种群规模N=60,学习因子c1=2,c2=4,惯性权重最大值wmax=2,最小值wmin=0.5,排挤因子CF=2,小生境半径r=1,最大迭代次数T=0。
首先采用改进的粒子群算法对LSSVM 的参数进行寻优,获得最优参数值:c=0.8,σ=1.2;然后采用测试数据进行诊断,得到8 组测试数据的诊断精度为100%,实现了数据的完全分类。
为了证明本文方法的优越性,将本文方法与文献[7]和文献[8]进行比较,得到的适应度随迭代次数变化的曲线如图1所示。
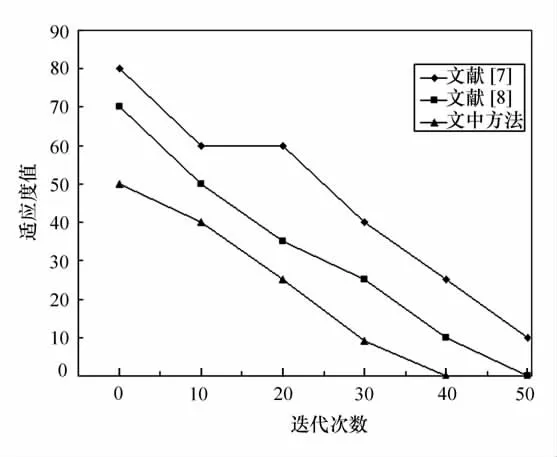
图1 适应度随迭代次数变化曲线
从图1中可以看出,文献[7]对应的适应度最差,本文方法和文献[8]分别在迭代40次和50次时达到了全局在最优值,这是因为文献[7]采用神经网络进行故障诊断,在小样本数据情况下具有较大的训练误差。本文方法由于采用粒子群优化的LSSVM 进行故障诊断,能克服训练小样本的不足,具有较强的泛化能力,且具有较快的收敛速度,所以在迭代到40次时就已经获得最优适应度。
4 结论
本文中提出了一种基于最小二乘支持向量机的飞机发动机故障诊断方法。为了提高最小二乘支持向量机的诊断性能,采用改进的粒子群算法对最小二乘向量机的正则化参数c和RBF宽度σ进行寻优,然后采用经过参数优化的最小二乘支持向量机用于飞机发动机故障诊断。试验结果证明:本方法能有效地实现故障诊断推理,克服了传统诊断方式的不足,是一种能有效进行故障诊断的新方法。
(
)
[1]郝英,孙健国,白杰.航空燃气涡轮发动机气路故障诊断现状与展望[J].航空动力学报,2003,18(6):753-760.
[2]Doel D L.Temper-A Gas Path Analysis T ool f or CommercialJ et Engines[J].Transact ions of the ASME Journal of Engineering f or Gas Turbines and Power,1994,116(1):82-89.
[3]鲁峰,黄金泉,陈熠.航空发动机部件性能故障融合诊断方法研究[J].航空动力学报,2009,24(7):1649-1653.
[4]张鹏,王婷婷,俞利明.改进的模糊Petri网在民航飞机故障诊断中的应用[J].测控技术,2011,30(4):70-73.
[5]王修岩,薛斌斌,李宗帅.基于Petri网的飞机交流发电机故障诊断系统研究[J].中国民航大学学报,2012,30(1):23-25.
[6]王久崇,樊晓光,万明,等.改进的故障树模糊诊断方法及其应用[J].计算机工程与应用,2012,48(14):226-230.
[7]宗慕洲,李学仁,杜军,等.基于相图-BP网络相结合的发动机转子系统故障诊断方法研究[J].计算机测量与控制,2012,20(8):2055-2060.
[8]胡金海,谢寿生,汪诚,等.基于粗糙核Fisher鉴别分析的特征提取及其在发动机故障诊断中的应用[J].航空动力学报,2008,23(7):1346-1352.
[9]Yuan Shengfa,Chu Fulei.Support vector machines-based fault diagnosis for turbo-pump rotor[J].Mechanical Systems and Signal Processing,2006,20(4):939-952.
[10]Eberhart R C,Kennedy J.A new optimizer using particle swarm theory[C]//Proc 6th Int Symposium on Micro Machine and Human Science,Nagoya,1995:39-43.
[11]Suykens J A K,Vandewalle J.Least squares support vector machine classifiers[J].Neural Processing Letters,1999,9(3):293-300.
[12]陈培友,李义玲.基于小生境遗传算法的自动谈判模型[J].计算机工程,2011,37(1):194-200.

