农产品多式联运网络优化研究

张 鑫，赵一飞

（上海交通大学中美物流研究院，上海200030）

中国是农业大国，随着农业的不断发展，其已经进入现代化发展阶段，对农产品的需求量不断增加，如何减少运输成本已成为农产品运输企业需要考虑的问题之一[1]。我国自20世纪90年代发展以来，运输中农产品物流的比例已经越来越大；而农产品公路运输是其最主要的方式[2]。

本研究通过对农产品多式联运和网络规划相关文献的研究，了解到目前该领域的研究现状，创新式将农产品多式联运引入传统单一公路运输方式来构建线性规划模型并对其进行优化，验证其有效性和可行性，最终得到预期的结果[3]。

1 问题及意义

1.1 问题的描述

农产品多式联运是生产商通过多式联运的方式对农产品进行运输，传统单一公路运输方式的流程如图1所示，即图1表示在有2个生产商和2个分销商的情况下，传统单一公路运输方式的流程[4]。

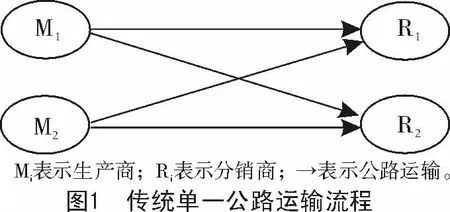
与传统单一公路运输流程不同的是，农产品多式联运在运输过程（图2）中会有铁路运输和水路运输2种方式可选择（每种运输方式都包括公路短驳运输方式，所以形成了多式联运）。而本研究的目的就是在传统单一公路运输方式上引入多式联运来对其运输总成本进行优化求解。

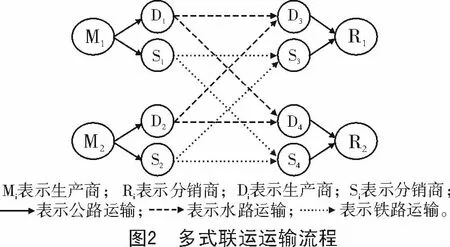
1.2 理论意义

目前网络规划模型已经是很成熟的模型[5]，在很多文献中已经有所体现。而农产品多式联运是一个相对新的课题，也进行了相关的研究，如王涛等[6]利用网络图论来对多式联运进行优化；王玲玲等[7]则通过遗传算法对多式联运的网络进行优化。但对农产品多式联运总费用进行网络线性规划的研究尚未见报道。本研究是创新式地将多式联运引入传统单一公路运输，并建立优化模型，从而对这种农产品多式联运网络的总成本进行优化[8]。

1.3 社会意义

农产品多式联运的课题虽然已经经过了一系列的研究，但是相应文献中使用的模型及相关理论比较复杂，而且计算量比较庞大，对于企业来说，使用这些模型会付出高额的时间和费用成本，所以并不经济[9]。而本研究通过网络的线性规划模型来解决这个问题，为企业提供一个快速且较低成本的选择。

2 模型描述

在如今行业竞争越来越激烈的现状下，对于物流成本的优化也成为企业决策的重要组成部分之一。传统的单一公路运输的物流成本依然很高[10]，通过结合多式联运和公路运输来决定最佳的运输路径及运输量，对于改善企业的利润状况有很大的帮助[11]。

2.1 传统单一公路运输模型

在传统的单一公路运输的情况下可以进行如下假设。

根据运筹学中运输问题假设：（1）在有m 个供货商（生产商）Mi发出货物（农产品），发货量为Ai（i＝1，2，3…m）。（2）有n 个分销商Rj接收货物Bj（j＝1，2，3…n）。（3）供货商（生产商）的供货量等于分销商的需求量，即：

（4）供货商Mi到分销商Rj的运货量为Xij，考虑到农产品的运输方式，则Xij为整数。（5）供货商Mi到分销商Rj费率为Cij。（6）设每条线路每种运输方式的最大承载量为Lij。这样可以得到传统单一公路运输的模型因变量Z 与自变量Xij的关系，即：

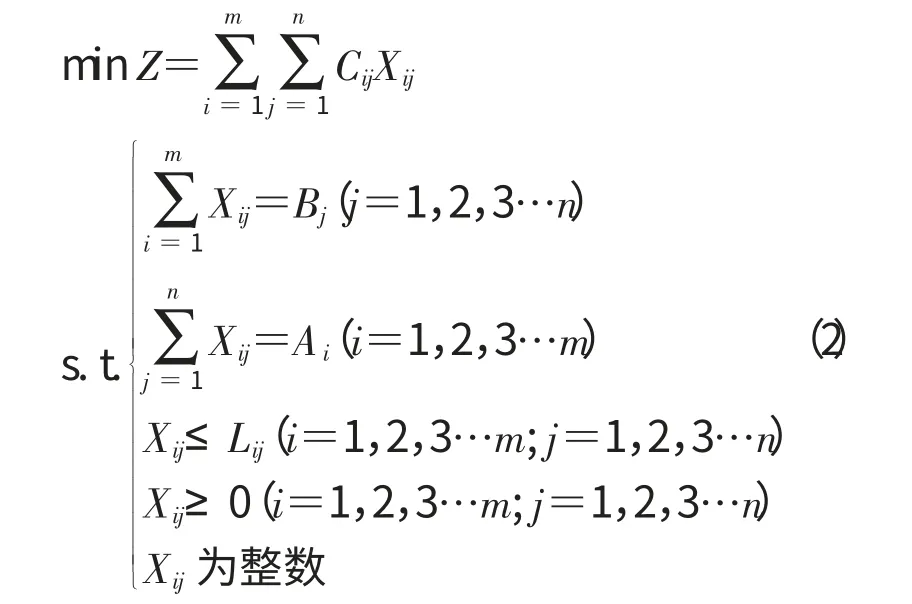
从式（2）可以看到，这是运输网络规划中的整数规划模型，是解决传统单一公路运输简单有效的模型，将引入水运和铁路运输的模型并进行对比。

2.2 引入多式联运的农产品运输模型建立

对于引入多式联运的情况下，模型假设如下。

如果要实现农产品多式联运，存在2种情况：第一，发货点和收货点存在水路运输的可能（即存在港口，或者发货点或收货点可以从附近的城市通过短途公路运输的方式来集货或配货），那么在这种情况下，点与点之间存在3种运输的方式，即水陆联运（水运加短途公路运输），铁陆联运（铁陆运输和短驳）和传统公路运输[12]。第二，发货点和收货点之间无法实现水陆运输，那么就只存在2种运输方式，即铁路运输和传统公路运输。

由于各种运输方式存在着费率的差异，也就为总成本优化提供了可能。

根据运筹学中运输问题假设：

（1）有m 个供货商（生产商）Mi发出货物（农产品），发货量为Ai（i＝1，2，3…m）。（2）有n 个分销商Rj接收货物Bj（j＝1，2，3…n）。（3）供货商（生产商）的供货量等于分销商的需求量，即：

（4）供货商Mi到分销商Rj通过第k（k＝1，2，3）（表示水路、铁路、公路运输方式）种运输方式的运货量为Xijk。（5）供货商Mi到分销商Rj通过第k（k＝1，2，3）（表示水路，铁路，公路运输方式）种运输方式的费率为Cijk，在实际中，对于农产品的运输在不同的运输方式下会有不同的费率，其中包含了水路、铁路和公路的运输费用以及为了达到码头或火车站所需要的短驳运输费用及相应中途仓储费用，这里把各种运输的费用整合到一起定义为该条线路上的费率Cijk。（6）设每条线路每种运输方式的最大承载量为Lijk。

根据上述的假设和约束条件，得到运输的供销平衡模型（模型Ⅰ）因变量Z 与自变量Xijk的关系。

模型Ⅰ的目标函数要使通过陆运、水运和铁路运输的单位费率与运量的乘积总和为最小，从而达到费率最优化的目的；而约束条件为：各个供应商发出的货物和分销商所需要的货物在相应的线路上相等，每条线路上的运输量（包括水路、铁路和公路运输）小于等于每条线路上的最大运输能力，每条线路的运输量都非负。

而在现实中，由于地区的消费能力不同以及季节性销售额的变化，总会出现供大于求或供不应求的情况，根据传统的运筹学中运输规划，可以得到2个相应的数学模型[13]。

在供大于求的情况下，生产商的供应量大于分销商的需求量，也就意味着各条线路上通过不同运输方式的运输量总和小于生产商的供应能力，得到优化模型（模型Ⅱ）因变量Z与自变量Xijk的关系。

在供不应求的情况下，生产商的供应量小于分销商的需求量，各条线路上通过不同运输方式的运输量总和小于该分销商的需求量，得到优化模型（模型Ⅲ）因变量Z 与自变量Xijk的关系。

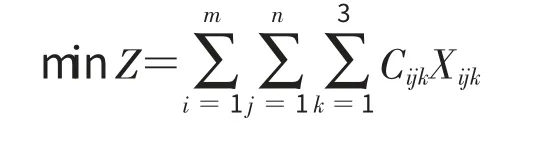
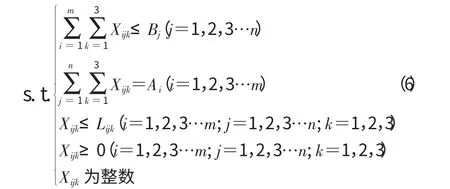
2.3 模型比较

在引入多式联运模型情况下，整数规划模型的复杂性增加，在实际求解中的计算量也增加，这是由于相对于单一公路运输的模型，多式联运模型生产商和供应商之间会多出水运和铁路运输的选择，这样也就会增加模型的计算量[14]。但如果水运和铁路运输的费率优于传统单一公路运输方式，模型也就可以使费率更加优化，也就实现了本研究的意义。

3 技术难点及解决方案

3.1 技术难点

在传统的单一公路运输模型中，由于农产品运输是直接从生产商到分销商，每条线路上的费率只需得到运距和相应线路的运价就可以得出[15]。而在农产品多式联运模型的使用中就要复杂许多，对于每条线路上的费率不但要得到运距的信息，而且包括各种费用，如两端的公路短驳运输费用，铁路运输和水运都是按班次运输，如果没有达到最低的运输量要求，那么也就会有农产品在火车站和码头的存放时间，相应也就带来了费用，而每一条线路上的相应费用又各不相同，这就增大了获取模型数据的难度[6]。

3.2 解决方案

虽然在实际的模型数据获得上存在难度，但是厂商可以通过了解供需状况，并且合理安排农产品的批次，使在火车站和码头的停放费用减少并且稳定，或者通过与承运人签订全程承运合同，使每条线路上的费率固定，这样也就解决了模型使用中的难点。

4 实例验证优化模型

为了证明模型的有效性，将传统单一公路运输和引入多式联运的运输成本进行比较。

4.1 传统单一公路运输方式

假设共有2个生产商和2个分销商，而每个生产商和分销商之间都有3种运输方式可以选择，每条运输方式都有相应的最大承载量Lij以及相应的费率Cij。这样就得到了2个生产商和2个分销商之间关于运量、承载量、费率的关系。假设数据如表1所示。

表1 传统单一公路运输方式下的试验数据

由表1得到这种情况下最优解为64.3万元，下面继续计算在引入多式联运方式情况下的算例结果。

4.2 引入多式联运的方式

假设共有2个生产商和2个分销商，而每个生产商和分销商之间都有3种运输方式可以选择，每条运输方式都有相应的最大承载量Lijk以及相应的费率Cijk。这样就得到了2个生产商和2个分销商之间每条线路关于运量、承载量、费率的关系。根据假设数据求模型最优解。

由表2可知，生产商和分销商之间每种运输方式的运价、运量，以及每种运输方式的最大承载量和每个生产商的供应能力，以及分销商的需求量。

表2 多式联运方式的试验数据

由表2假设数据来看，这是一个供大于求的问题，那么继续使用模型Ⅱ来对这个问题进行求解，得到表3的结果。

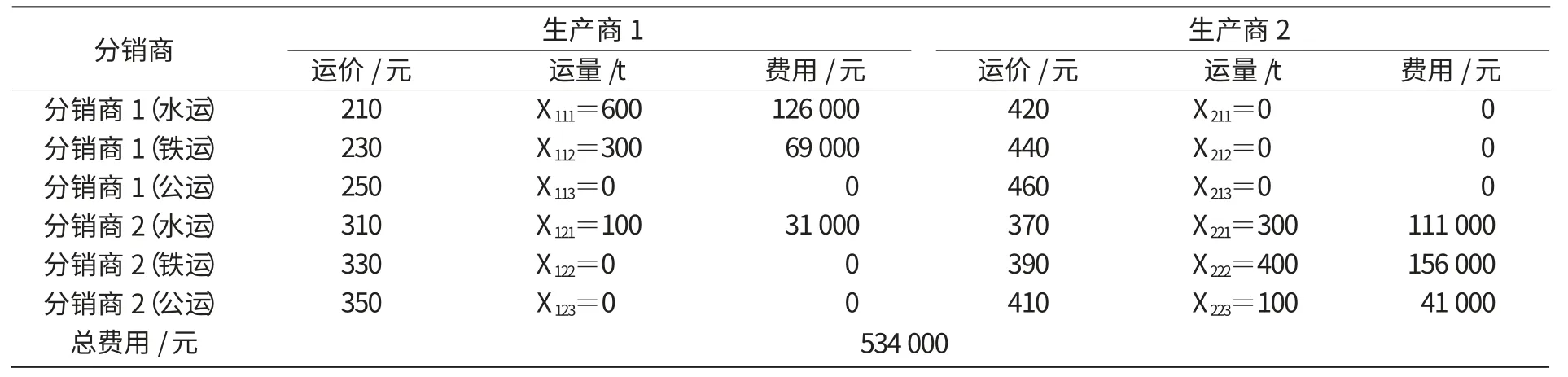
表3 多式联运方式的试验结果

根据表3的结果得到了2个生产商和2个分销商在引入多式联运的情况下，该模型的最优解为534 000元。

4.3 结果与比较

由2种情况的结果可以得到，如果铁路运输或水路运输的费率低于公路运输的线路存在，那么运输的总成本也就可以通过本研究描述的模型来进行优化低于传统单一公路运输成本，从而达到本研究所预期的结果。

5 结语

本研究创新式地对农产品多式联运网络进行线性规划优化，建立模型并证实模型的可行性，从而达到了预期的效果。但是农产品多式联运依然存在着其他的问题，例如在码头或仓库存放农产品的仓储问题以及农产品的保质期等问题，这将会随着课题的发展和研究而最终完善。

［1］朱静波.基于循环经济视角的农产品逆向物流运作模式与实施路径[J].湖北农业科学，2010，49（10）：2614-2616.

［2］凌中南.我国农产品物流产业的主要问题及对策[J].河南农业科学，2009（10）：6-7.

［3］运筹学教材编写组.运筹学[M].北京：清华大学出版社，1990.

［4］张京卫，张兆同.现代农产品物流发展对策研究[J].山西农业科学，2007，35（4）：7-10.

［5］姚裕华，叶耀华.供应链分销网络运输费率优化模型研究[M].物流技术，2004（10）：63-65.

［6］王涛，王刚.一种多式联运网络运输方式的组合优化模式[J].中国工程科学，2005，7（10）：46-50.

［7］王玲玲，覃运梅.多式联运的运输方案选择研究[J].铁道运输与经济，2009，31（10）：78-80.

［8］孙芸.发展农产品物流的对策研究[J].内蒙古农业科技，2009（4）：19-20.

［9］贾金凤，侯智惠.发展我国现代化农产品物流体系的制约因素及其对策[J].内蒙古农业科技，2005（S2）：358-359.

［10］沐士光.遗传算法在网络优化问题中的研究与应用[J].计算机仿真，2010，27（5）：128-131.

［11］姜平，魏霜.鲜活农产品物流发展策略[J].中国物流与采购，2010（3）：74-75.

［12］张建勇，郭耀煌.一种多式联运网络的最优分配模式研究[J].铁道学报，2002，24（4）：114-116.

［13］王巍，张小东，辛国栋.基于多式联运的组合优化模型及求解方法[J].计算机工程与应用，2009，45（7）：212-214.

［14］郭晔.农产品加工企业应急物流系统的研究[J].内蒙古农业科技，2012（2）：65-66，73.

［15］Modesti P.A utility measurefor findingmulti-objectiveshortest paths in urban intermodel transportation networks[J].European Journal of Operational Research，1998，111（3）：495-508.