基于插值方法的EMO 多样性保持策略

陈 琼，叶理德

(中冶南方工程技术有限公司技术研究院，湖北 武汉430223)

演化算法种群的多样性是指种群包含的个体不能过于单一，即种群中既要包含优秀的个体又要包含较差但有潜力的个体，尽可能地保留最终有潜力成为非劣解但因为选择机制而过早被淘汰的个体的基因，使它们有参与竞争演化的机会。多样性保持策略既要保证演化多目标优化算法［1－4］得到的非劣解集具有较好的分布性，也要兼顾算法的效率，使得算法具有较快的收敛速度。

在演化前期或某一代演化迭代结束后，由于非劣解数目缺乏，会出现导致算法搜索到的近似Pareto 前沿间断或不完整的现象。针对该现象，提出了基于插值方法的演化多目标优化多样性保持策略，其主要思想是在算法没有搜索到的新区域，进行内插或外推，引导算法在新区域进行搜索，期望算法搜索到更多更优质量的非劣解。

采用单一的性能评价方法对演化多目标优化算法的性能进行度量会产生偏差，而仅仅采用近似Pareto 前沿与Pareto 前沿的逼近程度或非劣解集的多样性，都不能全面地评价解的好坏［5］。因此，可采用收敛性，即转化的代间距离［6］(inverted generational distance，IGD)和多样性［7］(多样性熵)两个指标综合评价算法的性能。

1 插值方法

插值方法是根据算法搜索到的非劣解信息插入新解的过程。按照插入新解的位置，插值方法分为内插法和外推法，其中，内插法包含均值插值法和凸组合插值法。

均值插值的特点是对于任何一种曲线进行无限等分，两点之间的曲线可以用两点之间的直线近似代替。因此，在无限等分的情况下在两点之间的连线中点插入一个新个体就等同于在两点之间的曲线段上插入一个新个体。插入的新个体为算法在已知的两个非劣个体之间的区域上进行搜索提供了更多的机会，并为算法可能搜索到更多的非劣解创造了条件。

凸组合插值方法［8］是根据算法搜索到非劣解的信息，在两个非劣解之间的区域内进行搜索，引导算法开辟更多的搜索区域。

对Pareto 前沿曲线进行无限划分时，任意两个个体之间的曲线段可以视为一条直线段，但是，在插值过程中，若两个已知个体之间的距离过大，虽然可以利用均值插值在两个已知个体之间插入新个体，引导算法在其区域上搜索，但是当两个已知个体之间的距离过大时，两点之间的直线段和两点之间的曲线段不一致，使插入的新个体远离近似Pareto 前沿，可能导致算法的无效搜索。为了使插入的新个体尽量位于相应近似Pareto 前沿附近，借助于凸组合插值方法来进行插入新个体，以保持种群的多样性。

根据算法搜索到的一部分非劣解集信息，在其非劣解分布区域外插入新个体，为算法在非劣解外部的新区域内进行搜索提供了机会，引导算法搜索到更多的非劣解。

2 基于插值方法的演化多目标策略

插值策略主要是根据已知的非劣解，在其附近的区域插入新个体，使算法搜索到更多的非劣解，而在算法搜索到的近似Pareto 前沿非劣解集中，根据个体之间邻近距离的大小进行判断，无疑对算法进行插入新个体具有重要的指导意义。由概率论可知，以个体之间的邻近距离作为一个变量是服从高斯概率分布的，而插入新个体的情况，即两个非劣解之间或一些非劣解的外部区域内是否插入新个体，可以依据其累积分布函数表示，度量是否插入新个体。

有多种插值方法可以对算法搜索到的近似Pareto 前沿非劣解集插入新个体，如内插、外推、内插外推相结合等方法。另外，如果非劣解集的多样性较好，则不需要插入新个体。在任意两个非劣解之间或外部区域插入新个体之前，应该考量插入新个体的依据，判断是否要插入新个体。通过人为方式控制算法内插、外推或内插外推相结合插入新个体是非常困难的，也就是说，算法应该能够根据不同的情况采用相应的插值策略。因此，提出了自适应控制策略，对每次演化得到的近似Pareto 前沿上的非劣解集是否需要插入新个体进行评估，若需要插值，则进一步确定采取何种插值方法，如内插、外推和内插外推相结合。

图1 所示为自适应控制策略结构图，在某一演化迭代过程中，算法对当前搜索到的非劣解集进行评估，判断其是否需要进行插值，如需要插值，则需要判断当前迭代过程中所搜索到的非劣解集，需要进行的是内插、外推还是内插外推相结合，否则，不插入任何新个体，结束此次操作。插值策略不仅可以增强算法的多样性，保持找到的非劣解集尽可能均匀、离散地分布在近似Pareto前沿上，而且也可以加速算法的收敛速度。由于IGD 指标既可以度量算法搜索到的非劣解集的多样性，也可以度量算法的收敛性。因此可以用IGD 作为判断是否插入新个体的依据。

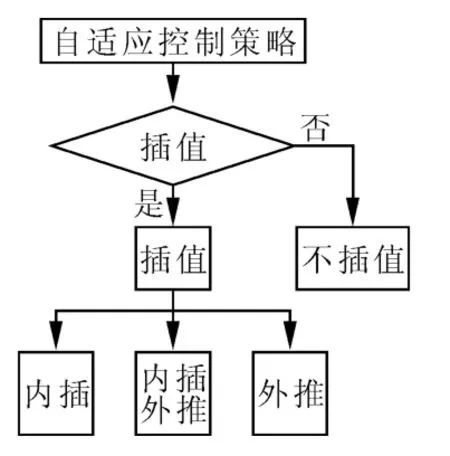
图1 自适应控制策略结构图

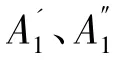
输入相关参数(种群P);输出种群P。

(1)从种群P 中，获取算法搜索到的非劣解集NDSet，并置dur=0 和IGD1=0;

(2)计算出非劣解集NDSet 的IGD 值;

(3)若|IGD1－IGD| ＜0. 01 或IGD1=0，则IGD1=IGD 且dur=dur+1，否则dur=0;

(4)若dur ＞Dur(Dur 为插值策略的间隔阈值)，则跳转至步骤(9)，否则继续下一步;

(5)对种群P 进行内插方法，生成新种群P1，并计算IGD 值得IGD1;

(6)对种群P 进行外推方法，生成新种群P2，并计算IGD 值得IGD2;

(7)对种群P 进行内插外推方法，生成新种群P3，并计算IGD 值得IGD3;

(8)在IGD1、IGD2和IGD3中，选择最小的IGD 值，并利用对应的种群替换种群P;

(9)输出种群P。

3 数值分析

基于层次聚类的演化多目标算法(hierarchical clustering model evolutionary multi－objective optimization algorithm，HCMEMO)［9－10］，采用插值策略后，称之为I－HCMEMO 算法。为了验证算法的有效性，在标准测试函数ZDT1 ～ZDT6 上做了实验，由于篇幅的限制，只列举了连续和非连续的ZDT1 和ZDT3 测试函数对NSGAII(dominated sorting genetic algorithm II)、HCMEMO 和I－HCMEMO 算法进行的测试结果，并通过多样性熵和IGD 指标对测试结果进行说明。

(1)ZDT1 问题求解。NSGAII、HCMEMO 和I－HCMEMO 算法对问题ZDT1 求解时的Pareto 前沿如图2 所示。由图2 可以看出I－HCMEMO 算法求解的近似Pareto 前沿完全覆盖了NSGAII 算法和HCMEMO 算法，因此，I－HCMEMO 算法的结果优于NSGAII 算法和HCMEMO 算法的结果。

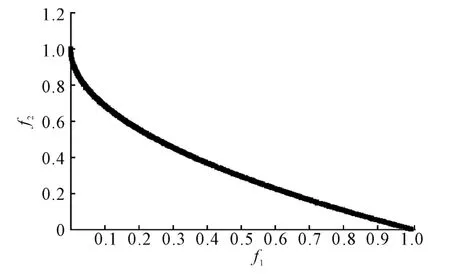
图2 ZDT1 的Pareto 前沿

NSGAII、HCMEMO 和I－HCMEMO 算法对问题ZDT1 求解时算法的多样性熵如表1 所示，可以看出:在演化的前期，种群的多样性相差不大，随着演化过程的进行，I－HCMEMO 算法求解的近似Pareto 前沿的多样性熵在40 代左右达到最大值，并趋于稳定状态，其效果明显优于NSGAII和HCMEMO 算法，但是I－HCMEMO 算法求解的近似Pareto 前沿多样性的波动比较大，后期的演化过程中，多样性的稳定性要劣于HCMEMO 和NSGAII 算法。

NSGAII、HCMEMO 和I－HCMEMO 算法对问题ZDT1 求解时算法的收敛性指标转化的代间距离IGD 如表2 所示，可以看出:I－HCMEMO 算法的IGD 指标值在演化的40 代左右开始趋于最小值，并呈现稳定状态，NSGAII 算法和HCMEMO 算法的IGD 指标趋于最小值，并呈现稳定状态，分别在60 代、100 代左右，但当NSGAII、HCMEMO 和I－HCMEMO 算法的IGD 指标都趋于稳定状态时，I－ HCMEMO算法的IGD指标要略高于NSGAII 算法和HCMEMO 算法的IGD 指标。因此，从整体上来看，在算法的收敛性上，I－HCMEMO 算法要略优于NSGAII 算法和HCMEMO 算法。

(2)ZDT3 问题求解。NSGAII、HCMEMO 和I－HCMEMO 算法对问题ZDT3 求解时的Pareto 前沿如图3 所示，由图3 可以看出HCMEMO 算法求解的近似Pareto 前沿完全覆盖了NSGAII 算法求解的近似Pareto 前沿，其结果要优于NSGAII 算法，而I－HCMEMO 算法求解的近似Pareto 前沿要明显低于HCMEMO 算法和NSGAII 算法，由标准测试函数ZDT3 的函数表达式可以看出，曲线越接近于原点结果越好。因此，I－HCMEMO 算法的求解结果要优于HCMEMO 算法和NSGAII 算法。

NSGAII、HCMEMO 和I－HCMEMO 算法对问题ZDT3 求解时算法的多样性熵如表1 所示，可以看出:随着演化过程的进行，I－HCMEMO 算法求解的近似Pareto 前沿的多样性熵处于较为剧烈的波动状态，在第100 代左右逐渐开始趋于稳定。当在20 代左右I－HCMEMO 算法的多样性熵值，开始达到最大值，但在40 代到80 代左右，多样性波动比较剧烈，并在180 代后，熵值又开始达到最大并高于算法在30 代左右出现的最大熵值，说明I－HCMEMO 算法与NSGAII 算法和HCMEMO 算法相比具有较好发现新解的能力。但从种群的多样性上考虑，I－HCMEMO 算法劣于于NSGAII 算法和HCMEMO 算法。

NSGAII、HCMEMO和I－HCMEMO算法对问题ZDT3 求解时算法的收敛性指标转化的代间距离IGD 如表2 所示，可以看出:I－HCMEMO 算法的IGD 指标值在演化的40 代左右开始趋于最小值，并呈现稳定状态，NSGAII 算法和HCMEMO 算法的IGD 指标趋于最小值，并呈现稳定状态，分别在40 代、80 代左右，但当NSGAII、HCMEMO 和IHCMEMO 算法的IGD 指标都趋于稳定状态时，NSGAII 算法的IGD 值要小于HCMEMO 算法的IGD值，HCMEMO 算法的IGD 值要小于I－HCMEMO算法的IGD 值。因此，在算法的收敛性上，NSGAII算法的收敛性要略优于HCMEMO 算法，而HCMEMO 算法的收敛性要优于I－HCMEMO 算法。

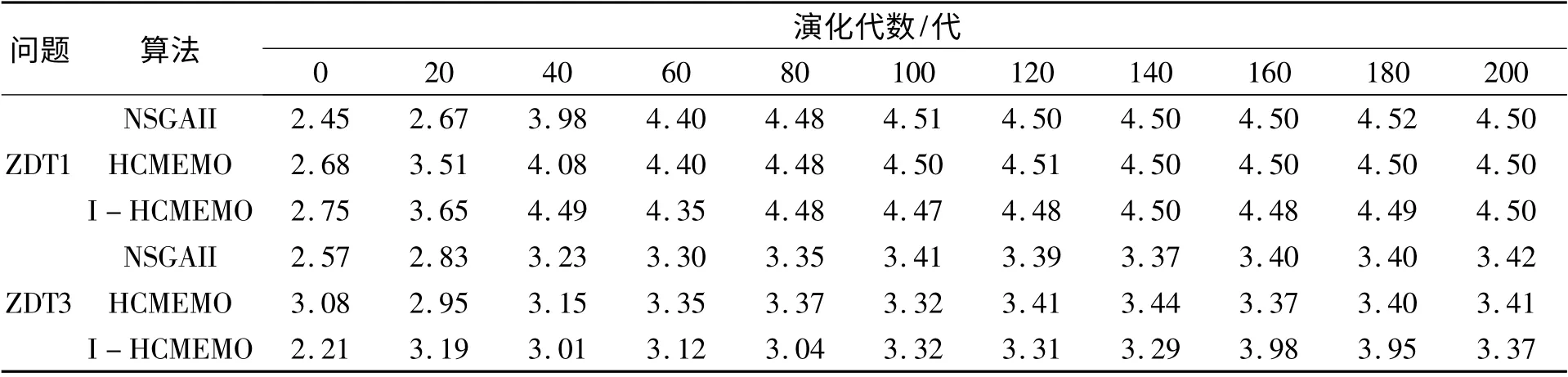
表1 NSGAII、HCMEMO 和I－HCMEMO 算法对ZDT1 和ZDT3 求解时算法的多样性熵

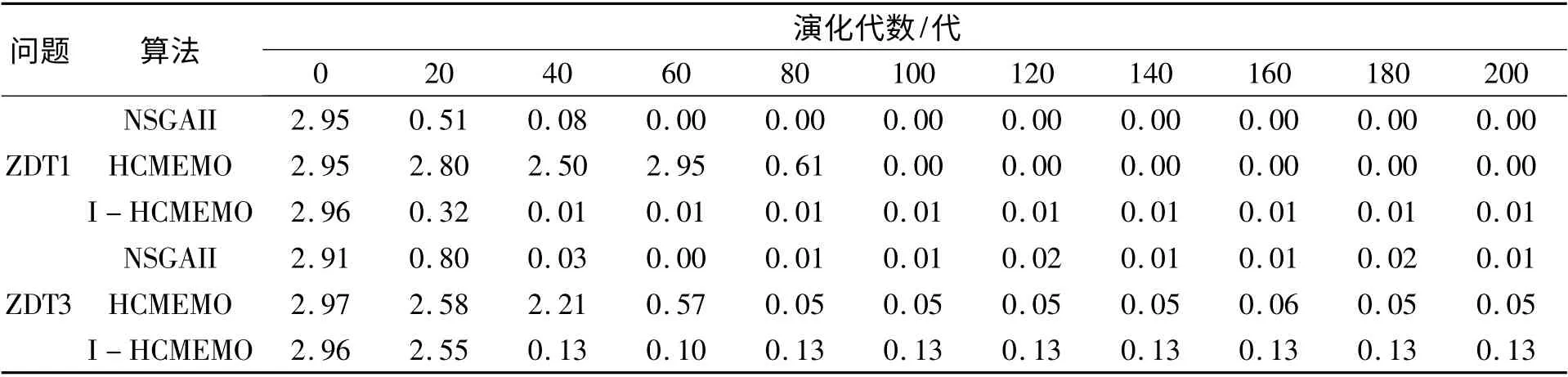
表2 NSGAII、HCMEMO 和I－HCMEMO 算法对ZDT1 和ZDT3 求解时算法的代间距离IGD

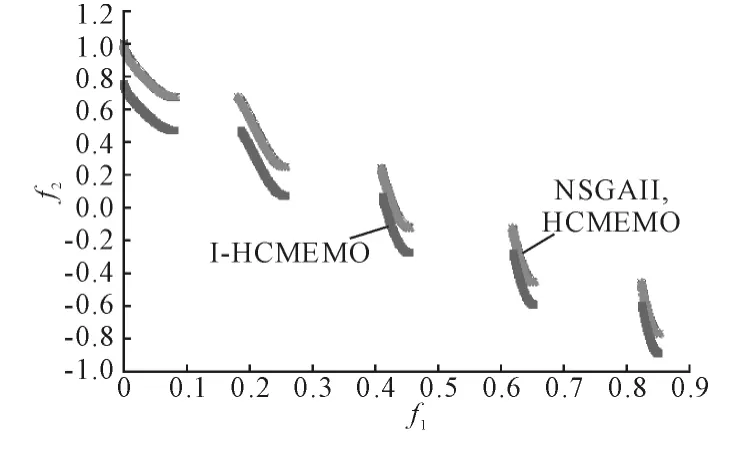
图3 ZDT3 的Pareto 前沿

4 结论

通过对插值方法的演化多目标优化多样性保持策略进行试验测试，从得到的多样性熵分析和IGD 指标分析的结果可以看出，基于插值策略的算法性能得到了明显改进，并优于NSGAII 算法和没有使用插值策略的多样性保持策略。

［1］ ZITZLER E，THIELE L，BADER J. SPAM:set pref erence algorithm for multi－objective optimization［C］∥Lecture Notes in Computer Science 5199.［S. l.］:［s.n.］，2008:847－858.

［2］ 崔逊学.多目标进化算法及其应用［M］.北京:国防工业出版社，2006:86－87.

［3］ VAN VELDHUIZEN D A，LAMONT G B. Multi－objective evolutionary algorithms:analyzing the state－of－ the－art［J］. IEEE Transaction on Evolutionary Computation，2000，8(2):125－147.

［4］ ZITZLER E. Evolutionary algorithms for multi－objective optimization:methods and application［D］. Zurich:Swiss Federal Institute of Technology (ETH)，1999.

［5］ 徐建伟，黄辉先，彭维，等.多目标进化算法的分布度评价方法［J］.计算机工程，2008，34(20):208－209.

［6］ LI H，ZHANG Q. Multi－objective optimization problems with complicated pareto sets，MOEA/D and NSGA－II［J］. IEEE Transactions on Evolutionary Computation，2009，13(2):284－302.

［7］ FARHANG－MEHR A，AZARM S. Diversity assessment of pareto optimal solution sets:an entropy approach［C］∥Proceedings of Congress on Evolutionary Computation (CEC’2002). Piscataway:IEEE Service Center，2002:723－728.

［8］ GARC＇IA A J，VERDEJO V G，FIGUEIRASVIDAI A R. New algorithms for improved adaptive convex combination of LMS transversal filters［J］. IEEE Tram Signal Processing，2005，54(6):2239－2249.

［9］ 吴帆，李石君.一种高效的层次聚类分析算法［J］.计算机工程，2004，30(9):70－71.

［10］ HU J，GOODMAN E D. The hierarchical fair competition HFC model for parallel evolutionary algorithms［C］∥Proceedings of the 2002 Congress on Evolutionary Computation.［S.l.］:IEEE Press，2002:49－54.