基于Adams的齿轮－齿条变幅驱动动力学研究

苏 艳，李涛涛，郭 燕

（武汉理工大学物流工程学院，湖北 武汉 430063）

四连杆门座起重机是当今最为通用的起重运输机械之一，广泛运用于各个码头。而齿轮－齿条变幅又是门座起重机最常用的一种变幅形式［1］。变幅机构齿轮－齿条在传统的设计方法中只保证轮齿的静强度符合要求，并且对于动态效应仅以安全系数来考虑，但在齿轮－齿条啮合过程中，齿轮与齿条的冲击振动十分严重［2－3］。随着现代设计方法的发展，有必要对齿轮－齿条进行动态研究。

以往的研究只建立齿轮－齿条啮合模型，不考虑外界因素影响［4－5］，并且齿条只作直线运动［6］。笔者研究的对象中齿条作曲线运动，齿条的运动可分解为以齿轮轴线为中心的转动和沿着齿轮切线方向的平动这两个运动，在该运动过程中，齿条运动瞬心的位置是随着时间不断变化的。针对这种特殊的运动形式，建立齿条做曲线运动的振动分析数学模型，并利用Solidworks软件及大型动力学分析软件Adams对其进行动力学分析，得到齿轮－齿条动态啮合力，为将来实现变幅机构齿轮－齿条动态设计提供理论基础。

1 齿轮－齿条刚体啮合振动分析模型

图1中，Ip为主动齿轮的转动惯量，Rp为主动齿轮的基圆半径，e为齿轮啮合综合误差，F为作用在齿条上的外载荷。kpy、kgy、cpy、cgy分别为支承箱体、支承轴的支承刚度与阻尼。km和cm分别为齿轮副啮合综合刚度和综合阻尼［7］。

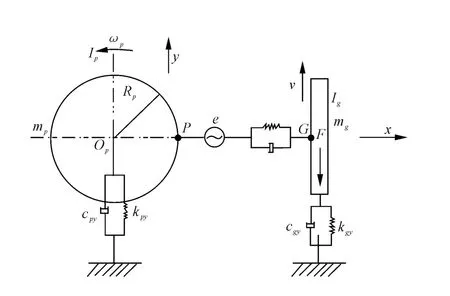
图1 齿条做直线运动时单级齿轮－齿条刚体啮合耦合振动模型

图1所表示的是主动齿轮带动齿条做直线运动的模型，该模型有3个自由度，分别为主动齿轮绕旋转中心的转动自由度和主、被动齿轮沿y方向的平移自由度，设这3个自由度分别为yp、yg、θp，则齿轮动态啮合力可以表示为:

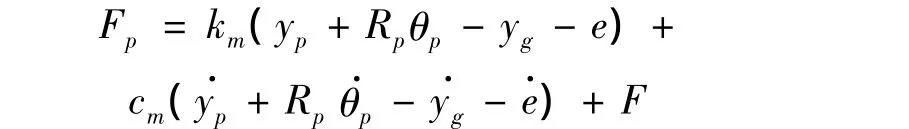
在变幅的过程中，当变幅齿条随臂架前后运动时，摇架会以驱动齿轮的圆心为轴摆动，齿条作以半径为轴心到齿条与齿轮接触线的距离圆的切线方向的运动，其模型如图2所示。图2中Q为齿条运动过程中某时刻的运动瞬心，其他符号意义与图1相同。该模型有4个自由度，除yp、yg、θp外还有θg。齿轮动态啮合力可以表示为:

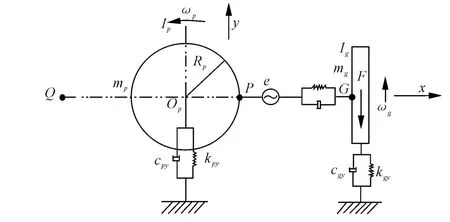
图2 齿条做曲线运动时单级齿轮－齿条刚体啮合耦合振动模型

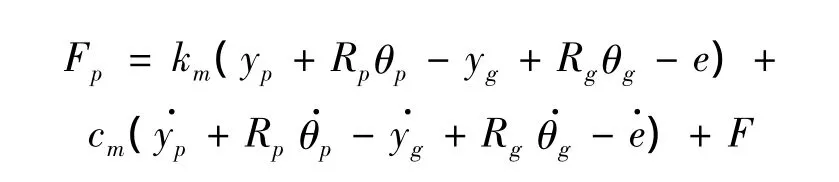
2 变幅机构动力学模型建立

2.1 动力学模型的建立

利用Solidworks对四连杆门座起重机的臂架系统、平衡梁、立柱、摇架及齿轮齿条进行几何建模并装配（如图3所示），将装配体保存为x－t格式，并将其导入Adams中（如图4所示）。在Adams中对模型加约束，在各个铰点处加铰接副，立柱加固定副。在Adams中由专门的齿轮副来进行齿轮啮合的模拟，但这仅限于运动学分析。为了模拟齿轮－齿条的真实运动情况以及得到真实的动态啮合力，在摇架与立柱之间加铰接副，齿条与摇架之间加移动副，小齿轮与立柱之间加铰接副，小齿轮与大齿轮之间加接触。笔者不考虑钢丝绳的变形，以圆柱模拟钢丝绳，赋予其质量并与象鼻梁之间加球铰副，将货物的质量加到球体上并与钢丝绳之间加球铰副（如图4所示）。

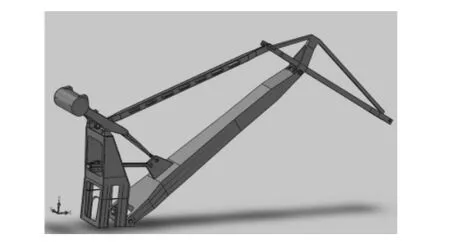
图3 基于Solidworks的变幅机构几何模型

图4 基于Adams的变幅机构模型

2.2 动力学设计参数

在Adams中仿真动态啮合力的关键是接触参数的设置和碰撞形式的确定。为了得到真实的动态啮合力，选择Solid-Solid实体碰撞，并根据Hertz碰撞理论确定齿轮与齿条的碰撞刚度K［8－9］，其计算式为:

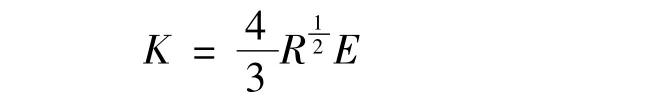
式中:1/R=1/R1+1/R2，R1、R2为接触物体在接触点的接触半径（由于齿高与齿轮分度圆半径相比较小，因此取小齿轮接触半径为分度圆半径，齿条的接触半径取为无限大）；1/E=（1－）/E1+（1 －）/E2，u1、u2为两接触物体材料的泊松比，E1、E2为两接触物体材料的弹性模量。由此可得碰撞刚度为:

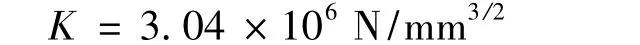
根据Hertz理论，碰撞力的大小主要由弹簧控制，因此阻尼系数C一般取得比较小或者忽略不计，取C=10 N·s/mm。碰撞指数e取1.5，阻尼完全作用距离 d 取 0.1 mm［10］。

3 仿真与结果分析

3.1 基于Adams的变幅机构运动学仿真

齿轮－齿条在变幅中会有一个加速与减速的过程，因此小齿轮的驱动用STEP函数来表达。在变幅的过程中，主要驱动是齿条力，去除小齿轮并在齿条与摇架的移动副上加上与齿条运动方向相同且运动线速度数值相当的移动驱动（如图5所示），测量齿条与臂架铰点的力，即臂架系统在变幅过程中所产生的力。通过这种方法仿真出臂架在变幅过程中所需的变幅力（如图6所示）。

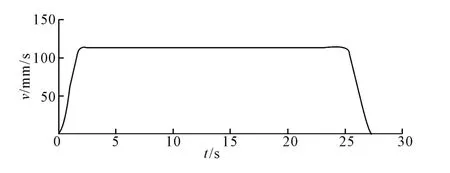
图5 齿条线速度－时间变化曲线

3.2 变幅机构动力学仿真结果与分析

利用Adams对模型进行仿真分析，可以得到齿轮齿条动态啮合力曲线，如图7和图8所示。

图7为齿轮齿条啮合力的真实曲线。图8为改变齿轮－齿条接触刚度后的啮合力曲线。可以看到图7中的啮合力周期变化，变化周期约为1 min，与实际相符。图6（a）和图6（b）是不同坐标系中的同一条曲线，图6（a）的纵坐标取值与图7一致以方便两图的比较。比较图6（a）和图7，可以看到图7的曲线波动较大，而图6（a）是一条比较平滑的曲线，这是因为齿轮与齿条在啮合过程中由于货物的偏摆及啮合间隙等原因导致啮合冲击，从而导致图7仿真曲线的波动。图8是改变齿轮齿条接触设置参数中的接触刚度后得到的曲线，可见其变化趋势与图6（b）完全一致。

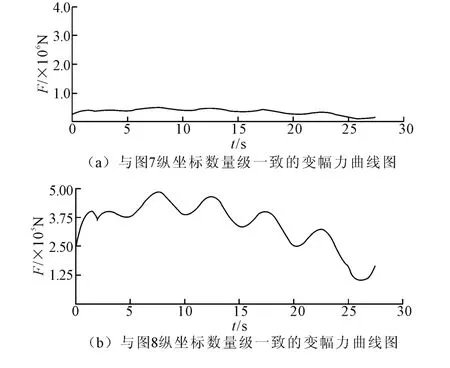
图6 变幅力曲线图

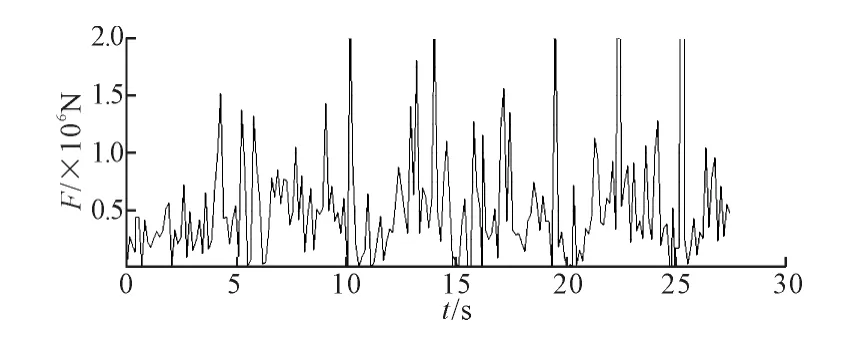
图7 齿轮齿条啮合力曲线图

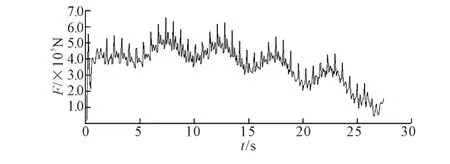
图8 改变接触刚度后的啮合力曲线图

4 结论

引入轮齿间碰撞、支承轴承及箱体的支承刚度等激励因素，建立了内部激励下的单级齿轮－齿条系统刚体啮合振动分析数学模型；对变幅机构进行系统性动力学分析与仿真，得到齿条做曲线运动的齿轮－齿条驱动机构在考虑啮合冲击及货物偏摆影响下的动力学曲线图，将其仿真结果与不考虑啮合冲击影响时的分析结果相比较，吻合度较高；研究原理及方法可借鉴到斜齿轮－齿条传动系统、蜗轮－蜗杆传动系统、非圆齿轮－齿条传动系统及混合式齿轮－齿条啮合系统等复杂传动系统中。同时，为齿轮－齿条机构的进一步优化设计、强度校核和振动噪声进行完整全面的分析提供了一种新的方法。

［1］张质文，虞和谦，王金诺，等.起重机设计手册［M］.北京:中国铁道出版社，1988:65－108.

［2］李勇智.齿轮变幅机构制动过程的动载荷分析［J］.港口装卸，2005（6）:1－2.

［3］丘水盛.齿轮齿条变幅驱动故障分析［J］.港口装卸，2002（4）:8 －9.

［4］徐方舟，魏晓辉，张明，等.基于Adams的齿轮齿条刚柔耦合啮合分析［J］.机械设计与制造，2012（7）:200－202.

［5］周旭辉，疏舒，马俊.基于Adams的小齿轮齿条动力学仿真分析［J］.船海工程，2012，41（5）:119－121.

［6］李宴，王瑾，徐皓，等.汽车转向器齿轮齿条的建模与仿真研究［J］.现代制造工程，2010（12）:73－76.

［7］李润方，王建军.齿轮系统动力学［M］.北京:科学出版社，1996:56－87.

［8］张争艳，张晶华，陆忠华，等.新型混合式多级串行行星齿轮减速器的动力学研究［J］.机械传动，2011，35（3）:11 －16.

［9］张争艳.自升式海洋钻井平台齿轮齿条爬升与锁紧系统设计与研究［D］.武汉:武汉理工大学图书馆，2011.

［10］龙凯，程颖.齿轮啮合力仿真计算的参数选取［J］.计算机仿真，2002，19（6）:87 －88.