模拟随机对照试验——一种新的用于疗效比较研究的统计分析方法

陈少科 赵 倩，2 张 羿，2 程 毅，2 曹 芳，2 严卫丽，2

近年来循证医学领域中疗效比较研究(comparative effectiveness research，CER)越来越受到关注［1］。CER 采用多种方法［2，3］，对“真实世界(real world)”中临床疾病不同治疗方法的治疗效果进行科学的分析比较，产生对临床决策有重要参考价值的证据［1］。对疾病治疗有关的观察性数据进行不同治疗策略或方法间的疗效比较分析时，平衡对比组间混杂因素和对偏倚进行定量的估计，是保障结果可靠性的重要手段，也是统计分析的最大难题。传统的控制混杂因素的方法有多因素的分析方法，倾向性评分(propensity score，PS)对于平衡对比组间混杂因素也很有帮助［4］。寻找更好的控制混杂因素的方法进行更加有效的疗效比较分析，一直是统计学、临床流行病学和循证医学专家研究的方向［5］。本研究探索发明了一种新的数据分析方法，通过对研究对象进行反复模拟随机化分组、借用RCT 的原理、应用新的统计量，对真实医疗过程中产生的疾病结局变量进行不同治疗方法之间的疗效比较分析，为临床决策提供一种新的证据类型，将之命名为模拟随机对照试验方法(simulated randomized controlled trials)，简称sRCT。

1 方法

1.1 设计原理 本研究设计原理如图1 所示。图1 描述了一个统计量odds 值产生的过程。图中浅绿色框架内为同一疾病状态下分别接受A(A 样本)或B(B 样本)治疗的患者经过100 次随机分组后每次的结局变量和混杂因素的处理方式;浅绿色框架外为经过100 次随机分组后结局变量的odds 值计算方式。需要说明的是:①图1 中A 样本和B 样本的样本量可以相等亦可不相等;②图1 中每1 次随机化分组后产生的两组样本与其实际接受治疗不符的理论概率为50%;③图1 中剔除的含义为:利用RCT 统计分析的符合方案集分析(per-protocol analysis，PP)策略，将每1次随机化分组后产生的两组样本与其实际接受治疗不符样本，即将分在A 组中的部分B 样本(图1 中用B－Bn表示)或分在B 组中的部分A 样本(图1 中用A－An表示)作为脱失处理;④由于每次随机化分组后利用PP 策略剔除了部分样本，可能导致混杂因素在组间失衡，故进行混杂因素组间均衡性比较，当100 次混杂因素假设检验结果中，拒绝H0的频数≥5 次，说明混杂因素组间不均衡为非小概率事件，不能用sRCT 进行结局变量比较分析，反之可以进行结局变量的比较分析;⑤根据检验假设的不同，对结局变量可以进行等效性检验、优效性检验或非劣性检验。

为了解统计量odds 值的理论分布，重复100 次图1 中一个odds 值产生的过程，可产生100 个odds 值。如果odds值的分布或者经转换后的分布符合或近似正态分布，可应用正态曲线下面积分布的原理计算odds 值的95%CI，实现对odds 值点估计值的假设检验。

以odds 值及其95%CI 作为最终判断不同治疗方式治疗效果是否存在差异的依据。当odds 值＜1 或其95%CI的上限＜1 时，认为两种治疗方式的治疗效果无差异。当odds 值＞1 或其95%CI 的下限＞1，认为两种治疗方式的治疗效果有差异。当odds 值=1 或其95%CI 包含1，暂时不能给出明确结论。

图1 odds 值计算过程示意图Fig 1 The diagram of calculation of odds

1.2 技术路线 通过对模拟数据库进行分析的方法说明sRCT 的原理、可行性、稳定性及判断结果与真实情况的一致性。以结局变量和混杂因素均为连续变量，每组样本量取50、100、500 和1 000，疗效分析以优效性检验为例。

1.2.1 数据库的创建 利用统计分析软件Stata 11.0 模拟研究对象接受不同治疗(实验组和对照组)的相关数据。并模拟创建疗效无差异数据库和疗效有差异数据库。每类数据库创建过程中均涉及3 个参数:样本量、把握度和效应量。

利用PS(power and sample size program)软件计算出上述两类数据库中不同样本量下(n1 = n2 =50、100、500 和1 000)，把握度(0. 5、0. 55、0. 6、0. 65、0. 7、0. 75、0. 8 和0.85)所对应效应量的大小(表1);再利用计算机模拟产生包含治疗方式、混杂因素(连续性变量)和结局变量(连续性变量)数据。以结局变量为例，进行疗效差异比较;以实验过程中可能存在的混杂因素为例，评价保留下来样本中的混杂因素在组间是否均衡可比。

表1 模拟数据库的特征:样本量、效应量和假设检验把握度Tab 1 Characteristics of simulated datasets:sample size，effect size and power

1.2.1.1 结局变量数据的产生 设定每组样本量为100、均数和标准差分别为27.5 和6，利用invnorm(uniform())* σ+μ 命令产生符合正态分布的实验组结局变量数据，并计算标准差。根据实验组结局变量标准差、把握度(0.50)和效应量(0.42)，产生符合正态分布的对照组结局变量数据。

1.2.1.2 混杂因素数据的产生 设定每组样本量为100、均数和标准差分别为174.5 和4，同样利用invnorm(uniform())* σ+μ 命令分别产生符合正态分布的对照组和实验组的混杂因素数据。由于未设定种子数，因此产生的实验组和对照组的混杂因素数据并不相等。

1.2.1.3 总数据库形成 利用stack、merge 等命令，将上述产生的实验组和对照组数据合并形成总数据库。

1.2.2 随机化方法 采用简单随机化分组方式，以记录号作为随机序列对总数据库进行随机化分组。

1.2.3 统计学分析 数据分析采用Stata 11.0 统计软件。计量数据以±s表示。两组间比较采用两独立样本t 检验，以α=0.05 为检验水准，P ＜0.05 为差异有统计学意义。

1.2.3.1 疗效差异比较 首先对总数据库进行100 次随机化分组，再根据PP 策略对保留下来样本中的结局变量进行假设检验(双侧检验)。检验假设为:H0:两种治疗方式治疗效果无差异;H1:两种治疗方式治疗效果有差异。根据100 次结局变量假设检验的结果，计算得到拒绝H0频数与不拒绝H0频数的比值(odds 值)。根据odds 值分布求得其95%CI。

1.2.3.2 混杂因素均衡性比较 ①两组样本量相等:对两组样本量相等且均为100 的总数据库进行100 次随机化分组，并对每次随机化分组后根据PP 策略保留下来样本中的混杂因素进行假设检验(双侧检验)。检验假设为:H0:混杂因素在组间均衡;H1:混杂因素在组间不均衡。然后分别计算出100 次混杂因素假设检验结果中拒绝H0和不拒绝H0的频数，以此作为判断混杂因素组间均衡性的依据。②两组样本量不相等:对创建的两组样本量分别为30和70 的总数据库进行100 次随机化分组，同样对根据PP策略保留下来样本中的混杂因素进行假设检验。最后分别计算出100 次混杂因素假设检验结果中拒绝H0和不拒绝H0的频数，以此作为判断混杂因素组间均衡性的依据。

2 结果

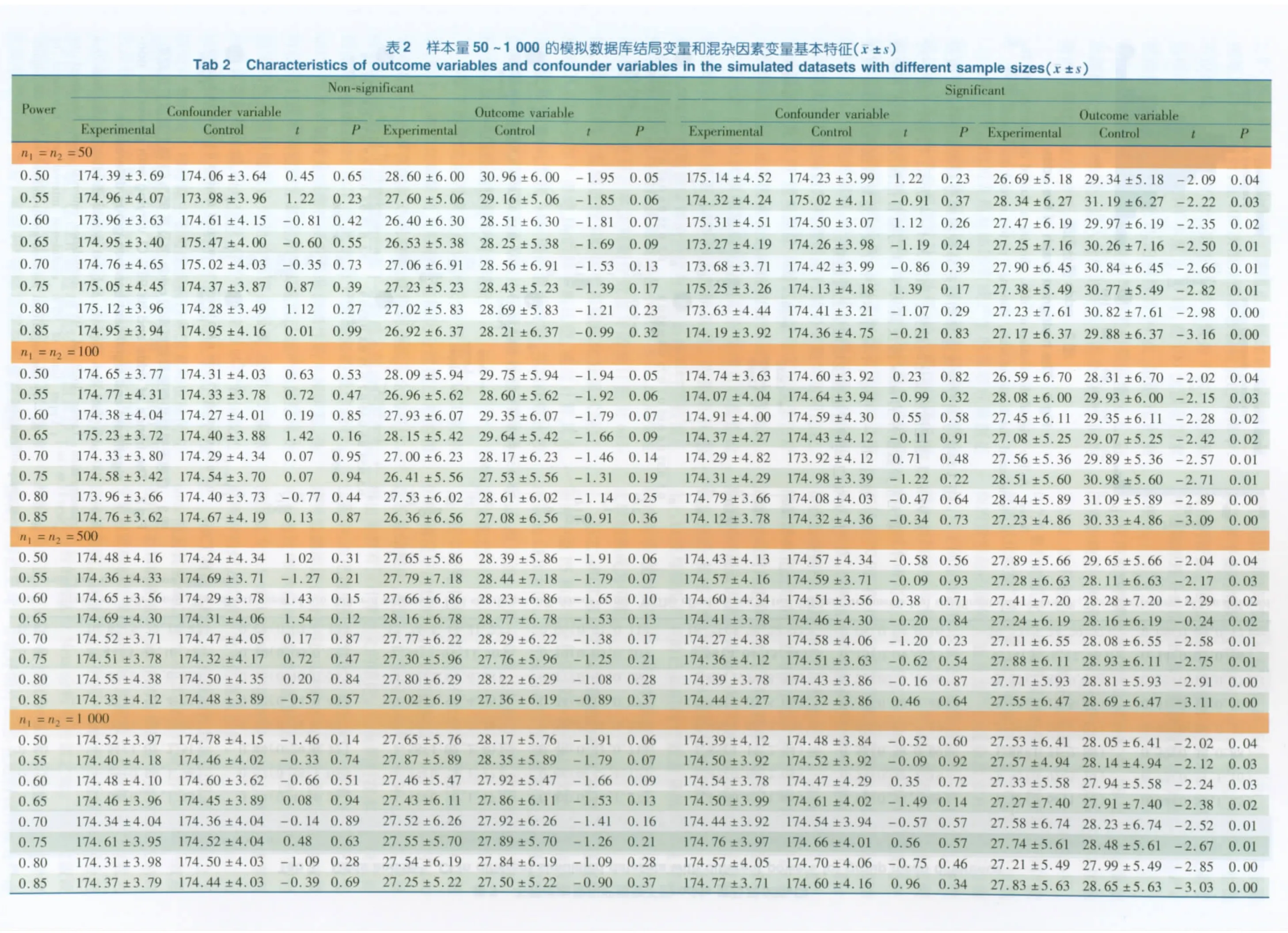
2.1 基本情况 表2 描述了根据表1 中的相应参数创建的每组样本量为50，100，500，1 000 时模拟数据库的基本特征。在数据库中，混杂因素在组间差异均无统计学意义(P ＞0.05);在疗效有差异数据库中，结局变量在组间存在差异(P ＜0.05);在疗效无差异数据库中，结局变量在组间差异无统计学意义(P ＞0.05)。

2.2 odds 值及其95%CI odds 值呈偏态分布(图2A)，对数转换后呈正态(图2B)，在此基础上根据正态分布曲线下面积分布的原理计算95%CI。表3 显示了对全部模拟数据库分析得到的odds 值及其95%CI。从表3 可以看出，对疗效有差异数据库分析得到的odds 值均＞1;对疗效无差异的数据库分析得到的odds 值均＜1。

?

?

图2 odds 值分布图Fig 2 The histogram graph of the odds

图3 描述了对疗效无差异和有差异数据库分析得到的odds 值及其95%CI 随把握度变化的趋势。如图3A1 ～4 所示，不同样本量中疗效无差异数据库的odds 值及其95%CI 均随着把握度增加呈下降趋势。如图3B1 ～4 所示，不同样本量中疗效有差异数据库的odds 值及其95%CI 均随着把握度增加呈上升趋势。

图3 疗效无差异和有差异数据库的odds 值及其95%CI 随把握度变化趋势Fig 3The trends of odds and its 95% CI varying with power for nonsignificant and significant between-group differences

2.3 混杂因素组间均衡性 当模拟数据库的两组样本量相等且均为100 时，在100 次混杂因素假设检验的结果中，不拒绝H0的频数为97 次，拒绝H0的频数为3 次。当实验组样本量为30、对照组样本量为70 时，在100 次混杂因素假设检验的结果，不拒绝H0的频数为99 次，拒绝H0的频数为1 次。说明当两组样本量相等和不相等的情况下，每次随机化分组后无错分进入分析的样本中混杂因素组间均衡的可能性均超过95%。

3 讨论

sRCT 设计的初衷是对临床实践产生的观察性数据进行疗效比较分析时，采用新的方法对可能引起偏倚的潜在混杂因素进行科学合理的统计学处理，最大限度地降低混杂偏倚对疗效比较分析的影响，从而为临床决策提供值得信赖的和较高水准的研究证据。sRCT 对混杂因素的处理借用了RCT 研究的原理，即通过“事后”的模拟随机化分组使混杂因素在组间达到均衡后进行结局变量的组间比较。考虑到采用类似PP 策略删除了随机分组与实际接受治疗矛盾的数据后，混杂因素在组间的均衡性可能遭到破坏，sRCT 设定了100 次模拟随机化分组后混杂因素均衡性检验拒绝H0的频率是否＜5%作为判断依据。当拒绝H0的频率＜5%时，说明删除理论治疗与实际治疗不符的数据后混杂因素在组间均衡性遭到破坏是小概率事件，结局变量的比较才得以进行。本文判断疗效差异的统计量为odds值，是针对同一案例进行100 次模拟随机化分组试验后，拒绝H0的频率和不拒绝H0的频率的比值，通过计算其点估计值和95%CI，实现odds 值的假设检验，并对疗效比较的结果进行解释。sRCT 方法可应用于优效性检验、等效性检验以及非劣效性检验等不同的情况。

sRCT 均衡混杂因素在组间的分布借用了RCT 的原理，RCT 是将研究对象纳入后通过随机化分组使已知的和未知的混杂因素在组间达到均衡，使组间达到完全的可比，疗效比较的差异可以肯定地归因于分组后不同治疗所产生的差异，前瞻性的RCT 因此成为干预研究的最佳设计。sRCT 的基本属性是观察性研究而非前瞻性的干预研究，是对临床实践不同治疗方案或方法实施后已经产生的结局变量采用反复模拟随机化分组均衡混杂因素、应用PP 策略和计算新的统计量odds 值及其95%CI 来反映疗效比较的结果和假设检验。sRCT 与RCT 不同之处在于:①RCT 的研究对象的纳入和排除主要考虑疾病诊断因素和试验的安全性因素，后者的考虑常使其限制过于严格。而sRCT 研究是临床已产生的数据，研究对象已经接受过治疗，因此纳入仅需考虑对疾病诊断和治疗的定义，对特殊人群如幼儿、孕妇等没有特别限制。②CER 的过程是对混杂因素作斗争的过程。sRCT 理论上将产生一半的研究对象其分组与实际接受的治疗相反，采用PP 策略后混杂因素在组间均衡性是进行结局变量比较的先决条件。sRCT 仅适用于混杂因素平衡的情况，这样的设计可以杜绝滥用数据，产生低质量的证据。通过模拟两组样本量相等或不相等，证明了PP 策略原理分析混杂因素均衡性被破坏的概率很小(P ＜0.05)。

应用观察性数据的疗效比较研究中，PS 也是排除混杂因素影响的一种常用方法［6，7］，PS 方法中以匹配法应用最为广泛，但不论是全局匹配还是局部匹配(卡钳匹配)［8］，均为“事后随机化”，均衡可观测的和已知的变量，达到“接近随机化数据”的效果，但对观察性数据中潜在的未知混杂因素引起的偏倚无能为力［9］。混杂因素在组间不均衡性，与不同组间的样本量是否相等可能有一定的关系，本研究中当两组样本量相等情况下混杂因素组间分布是均衡的，同时本研究也尝试了当实验组样本量为30、对照组样本量为70 时，在100 次混杂因素假设检验不拒绝H0的频率为99 次，说明组间样本量不相等情况下混杂因素组间分布也是均衡的，说明sRCT 虽然也是“事后随机化”，但通过模拟随机化分组的方法均衡了潜在的混杂因素。而PS 受观察组和对照组样本量的限制，较难实现充分的匹配以消除组间的混杂因素不均衡。sRCT 通过模拟数据和反复的模拟分析，描述了统计量odds 值的分布特征(对数正态分布)，以及与模拟产生的已知组间疗效差异结果的良好的线性关系，使计算odds 点估计值及其95%CI 来判断疗效比较结果成为可能。

总之，sRCT 吸收了RCT 思想的精髓，期望作为观察性研究中继PS 和多元分析后，又一种可以有效控制混杂因素的新的CER 方法。该方法尚有待于理想的真实数据加以验证，但开创一种用于观察性数据疗效比较研究的新方法，意义重大。

在本研究中未模拟创建不同样本量下把握度为0.9 和0.95 情况下的数据库，因为当把握度为0.9 或0.95 时，100次检验结果中，按照α 的检验水准平均有90 或95 次能够得出差异有统计学意义的结论。与此同时在本研究预实验过程中，对把握度分别为0.9 和0.95 疗效有差异/疗效无差异数据库进行分析时，在100 次结局变量假设检验结果中有超过95 次的结果是拒绝原假设/不拒绝原假设。即当把握度为0.9 或0.95 时，利用sRCT 有超过95%的概率判断两种治疗方式治疗效果的真实差异。

sRCT 有以下特点:①有效的控制混杂因素。②建立了odds 值及其95%CI 作为sRCT 的统计量，作为判断疗效是否存在差异的依据。odds 值的计算原理为通过100 次结局变量假设检验结果中拒绝H0的频数与不拒绝H0的频数之比计算得到。这种针对多个同一目的假设检验结果综合进行二次分析的做法与Meta 分析有类似之处。较单次假设检验结果而言，用odds 值及其95%CI 来判断疗效差异更精确，可靠性更高。③较好的外延性:在进行设计较为严谨的临床试验前，需按照严格的纳入排除标准选择研究对象，使得研究结论的应用人群受到限制［10］。而本研究是对基于真实医疗过程中产生的数据进行分析，研究对象为一组同一疾病状态下分别接受两种不同治疗的患者，这些研究对象的选择可能经过或未经过严格的纳入排除标准的筛选，因此运用sRCT 分析得到的结论将会适用于更广的人群。④小样本量即可实施:对每组样本量分别为50 和1 000疗效有差异数据库分析得到的odds 值均＞1，odds 值及其95%CI 均随着把握度的增加呈近似线性上升趋势。相反，对每组样本量分别为50 和1 000 疗效无差异数据库分析得到的odds 值均＜1，odds 值及其95%CI 均随着把握度增加呈近似线性下降趋势。一方面说明sRCT 稳定性较高，同时也说明sRCT 在样本量较小的情况下也适用，当然更小的样本量有待今后进一步尝试。⑤结局指标的确定:在前瞻性研究设计阶段需要明确定义研究的主要和次要结局指标，因此研究结果只能表明待研究治疗方式对某个特定结局指标的疗效，sRCT 可根据临床研究目的的不同，对观察性数据中两组均存在的结局指标进行分析，可根据临床需要选取关注的结局指标。

本研究中无论模拟数据库两组样本量是否相等，每次随机化分组后根据PP 策略进入分析的样本中，混杂因素组间均衡的频率都超过了95%，混杂因素在组间不均衡的可能性非常小，均提示能进行后续的疗效分析。但模拟数据与真实临床数据仍有区别，仍需复杂环境下的临床真实数据验证，仍有很长的探索之路要走。

作者已将sRCT 实现过程编写为Stata 11.0 可执行的do 文件，有意索取者请与本文通讯作者联系。

［1］Marko NF， Weil RJ. An introduction to comparative effectiveness research. Neurosurgery，2012，70(2): 425-434

［2］Armstrong K. Methods in comparative effectiveness research. J Clin Oncol，2012，30(34): 4208-4214

［3］Sox HC， Goodman SN. The methods of comparative effectiveness research. Annu Rev Public Health，2012，33:425-445

［4］Rosenbaum PR， Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika，1983，70(1): 41-55

［5］Concato J， Peduzzi P， Huang GD， et al. Comparative effectiveness research: what kind of studies do we need？ J Investig Med，2010，58(6):764-769

［6］Austin PC， Grootendorst P， Anderson GM. A comparison of ability of different propensity score models to balance measured variables between treated and untreated subjects:a Monte Carlo study. Stat Med，2007，26(4):734-753

［7］Austin PC. A critical appraisal of propensity-score matching in the medical literature between 1996 and 2003. Stat Med，2008，27(12): 2037-2049

［8］Austin PC， Mamdani MM. A comparison of propensity score methods:A case-study estimating the effectiveness of post-AMI statin use. Stat Med，2006，25(12): 2084-2106

［9］Brookhart MA， Schneeweiss S， Rothman KJ， et al. Variable selection for propensity score models. Am J Epidemiol，2006，163(12): 1149-1156

［10］McLeod RS， Wright JG， Solomon MJ， et al. Randomized controlled trials in surgery: Issues and problems. Surgery，1996，119(5): 483-486