创新投入强度与企业规模——基于分位数回归方法

闫 强

一、引言

1912年熊彼特(Schumpeter)提出的技术创新概念，以及此后所形成的关于企业创新理论，已经过近百年的发展。其中，技术创新与企业规模的研究文献众多，很多学者试图从技术创新的贡献角度探究到底是大型企业的贡献大还是中小型企业的贡献大，但至今仍未达成共识，而且熊彼特本人的观点前后也并不一致。技术创新与企业规模之间的关系一直没有得出确定性结论，也使得这一问题成为了熊彼特创新学派长期争议的焦点。

围绕“熊彼特假说”(Schumpeter’s Hypotheses)，经济学界的相关研究主要集中于支持企业创新投入与企业规模之间存在正相关关系以及两者之间呈现简单的正相关关系，后一种观点认为两者之间存在“U”型关系、“倒U”型关系或负相关关系。国外大量的实证研究揭示了企业规模和创新活动之间的正向关系。如Scherer指出，企业创新成果随企业产值的增长而增加，但通常增加的比率是递减的。[1]Scherer还发现研发同企业规模之间的关系接近线性，但对规模最大的企业有一定的凹性。[2]Cohen、Levin发现企业物质规模和行业性质对企业的R&D活动有重大影响。[3]Cohen、Klepper开创性地指出了企业R&D资本投入强度与企业诸如物质规模、现金流和多元化经营程度等特征有关。[4]Cohen、Klepper从研发成本分摊角度构建了理论模型,并通过实证检验表明,经营单位规模对经营单位R&D支出有显著正影响。[5]Kumar、Saqib通过调查和实证研究发现企业研发支出同规模呈正相关关系。[6]Yasuda、Takehi以日本制造企业的微观数据证明了公司规模等对公司成长中的R&D 行为存在着确定性影响。[7]国内关于创新投入强度与企业规模效应的研究并不多见,尤其是利用微观企业数据进行计量分析的实证研究就更少。柴俊武、万迪昉以西安市近800家企业为研究对象,应用结构方程模型进行了相关研究,发现企业创新物质资本投入与企业规模之间呈“倒U”型关系。[8]朱恒鹏使用国内10个省市800余家民营企业的调查数据，通过计量分析发现企业规模与民营企业研发支出强度之间呈现较明显的“倒U”型。[9]安同良等以江苏省制造业企业为样本,考察企业所处行业、企业规模以及企业所有制等因素对企业R&D 行为的影响,发现江苏小公司、中型公司、大公司的R&D 强度趋势存在着明确的倾斜的V型结构关系。[10]罗绍德、刘春光以制造业为样本研究发现研发投入强度与企业规模成反比。[11]孙晓华、田晓芳运用2006年中国37个工业细分行业的面板数据，考察了企业规模、市场结构、产权结构和资本密集度等因素对创新能力的影响，认为企业规模、市场结构与创新能力之间呈现明显的“倒U”型关系。[12]刘小元、李永壮基于中国创业板企业的数据发现企业规模与研发强度显著正相关。[13]

值得注意的是，这些研究基本都是基于企业微观数据，从企业技术创新经费投入角度出发，来检验企业规模与企业技术创新经费投入之间的线性因果关系，并且所采用的定量方法主要是运用一般的回归方法(包括OLS方法、离散选择模型方法和面板数据模型方法等)，从条件期望的角度分析企业规模与企业技术创新经费投入之间的关系与特征，但缺乏从企业规模对于创新投入强度的异质性边际影响角度进行分析，从微观层面检验熊彼特关于技术创新能力与企业规模之间的关系，并据此分别考察企业各种水平创新活动的经费投入强度与人力投入强度随企业规模的变化效应、特征及相互关系，就具有极为重大的现实意义。然而，目前国内极少见从技术创新投入角度出发，运用能够揭示企业规模对于创新投入强度的异质性边际影响的分位点回归方法，来对企业创新投入强度与企业规模之间的关系特征进行深入研究。因此，本文采用分位数回归方法进行实证分析，并根据相关结果更加全面地解释、说明与完善熊彼特(Schumpeter)关于技术创新能力与企业规模之间的关系，以求丰富该领域的研究内容。

二、理论分析

R&D一般被用来代表知识资产的投资情况。熊彼特明确指出，创新是一种经济活动，具有独特的经济因素和影响。

熊彼特认为技术变革是一个创造性的破坏过程。潜在的典型创新者为新成立的小公司，这些小公司受到的阻止非价格竞争(例如产品创新)的协议约束较少。[14]此外，为了保持活力，其遵循创新战略的激励更大。因此，小公司可以有更多的创新。

熊彼特强调技术变革是一个创造性的积累过程。[15]新创新者的作用是有限的，少数公司将市场分割为一个稳定的寡头垄断市场。规模较大的公司较之小公司，更具市场力量，因而在创新时处于优势地位，即市场力量是创新的必要条件，公司应该具有某种形式的事后市场力量，以防止仿制的新产品和新工艺，从而能够收回R&D投入。大公司由于在确保法律保护上也更具优势，这也将提供充足的短期市场力量，从而有效激励R&D投入。若无任何保护，大公司可能不会投资于创新活动，也就没有技术改变。事前的市场力量能有效降低R&D投资的不确定性破坏激励，从而有利于创新。基于上述分析，熊彼特认为，只有大公司可以诱导技术变革，因为在竞争如此激烈的环境中，小公司将资源花费在R&D上过于危险。

此外，Galbraith和Kraft认为，规模较大的公司有大量的R&D项目，因此更具分散风险的能力。[16-17]如果不同的项目成功的概率是不相关的，那么研究和开发项目的风险会随着项目数量的增加而降低。因此，公司规模越大，研究和开发项目的风险越小。竞争力较小的企业可能有更强的风险规避性，在项目融资时有更大的困难，从而无法充分获得创新活动的收益。

三、模型设定与变量选取

1.分位数回归方法

自Koenker和Bassett[18]首次提出分位数回归(Quantile Regression)方法以来，其在经济学实证研究中得到了广泛应用。传统的OLS方法有着极为严格的约束条件，并且当样本存在异常值时，对回归结果的影响较大。另外，OLS方法仅能度量自变量对于因变量的平均边际效应，无法得到自变量处在不同水平时，对因变量所带来的不同程度的影响。分位数回归方法的假设约束条件则更为宽松，尤其当误差项为非正态分布时，分位数回归估计量更为有效、稳健。可以说，分位数回归方法弥补了传统OLS方法的诸多不足。同时，该方法还可以度量自变量对于处在特征分布不同位置的应变量的异质性作用。

分位数回归模型一般表达式如下：

Qτ(Y|X=x)=x′β(τ)

(1)

其中，Qτ(Y|X=x)为给定自变量X=x时被解释变量Y的条件τ分位数，β(τ)是对应被解释变量的第τ分位数的回归系数向量，x是解释变量向量，τ是被解释变量的分位点。

(2)

这里ρτ(·)是检验函数(checkfunction),有

ρτ(yi-xi′β)=(yi-xi′β)(τ-I(yi-xi′β<0)),

I(·)为示性函数

由式(2)可知，分位数回归是采用加权残差绝对值之和的方法来对系数进行估计，对模型中的误差项不需做特别假定。分位数回归方法的本质是通过分位点τ取0，1之间的任何值，调节回归平面的位置和方向，估计因变量在不同分位点的回归系数。它在一定程度上可代表所有样本的信息，但更侧重于具有较大异质性的样本数据。

Koenker将分位数回归方法运用于面板数据模型估计中，并提出了具体估计方法及相关理论证明。[19]面板数据分位数回归模型能够较好地结合面板数据模型与分位数回归的各自优点,较之一般线性面板数据模型，面板数据分位数回归模型约束条件更少，对异质性更具包容性，估计的稳健性更高，估计所得系数更具显著性，回归分析结果也更为可信。

一般情况下，面板数据分位数回归模型表达式如下：

Qτ(yi,t|xi,t,zi,t)=α(τ)i,t+xi,t′β(τ)i,t+zi,t′γ(τ)i,t

(3)

由于我们的样本数据是混合截面数据，因此我们采用混合横截面分位数回归模型，形式表述如下：

Qτ(yi,t|xi,t,zi,t)=α(τ)+xi,t′β(τ)i,t+zi,t′γ(τ)i,t

(4)

其中，Qτ(yi,t|xi,t,zi,t)是给定解释变量xij,zij时因变量Y的条件τ分位数，βτ是对应因变量的第τ分位数的回归系数向量，xi,t,zi,t是自变量向量，ατ为截距项。

2.变量选取与模型设定

一般文献中，衡量企业创新投入强度的变量基本为创新活动经费支出或创新人力投入，而衡量企业规模的变量则包括企业从业人数、销售收入以及资产。本文在模型设定时则采用企业创新经费投入强度(企业科技活动经费内部支出占销售收入的比例)来作为被解释变量。考虑到创新经费投入强度变量使用了企业销售收入*此处，我们采用朱平芳、徐伟民所设定的方法，对历年销售收入和科技经费筹集总额进行价格平减。具体而言，将价格指数设定为消费物价指数和固定资产投资价格指数的加权平均值，两者的权重分别为O.55和O.45,进而得到实际值。[20]，此处设定的企业规模变量将选择企业从业人数。

在解释变量中，除了企业规模外，我们还加入了一些控制变量：(1)熊彼特经济增长理论认为追求垄断利润的企业是推动创新和技术进步的重要力量，因此，我们可以认为当期企业利润的获得，即企业盈利能力，对于下一期技术创新存在较大影响作用，选取上期的销售利润率作为解释变量也就较为合理。(2)如前所述，我们采用企业从业人员数代表企业规模，为了检验企业规模与创新投入强度之间是否存在非线性关系，我们将企业规模的二次项也作为解释变量加入到模型之中。(3)人作为创新活动中的主体，其支出成本直接关系到企业生产成本的变动。人力成本上升，一方面会增加企业运营压力，另一方面，也会倒逼企业采取各项积极方式，提高其技术创新能力，以维持企业持续发展。这里我们选取人均工资作为衡量人力成本的重要变量。(4)创新经费筹集能力的强弱直接影响到企业创新投入，并且由于创新活动的高风险以及企业融资困难，经费筹集能力较强的企业，其创新活动投入也相应较多，因此我们选取了企业科技活动经费筹集总额这一变量，对经费筹集能力与研发投入强度的关系加以考察。(5)企业在不同年份，可能会因为受到不同的经济政策、制度和环境变化等复杂因素的影响，引起创新投入强度发生改变，为此我们加入时间这一变量，以求得到不同年份对于企业创新活动的影响情况。综合以上分析与说明，模型变量定义见表1，具体模型设定如式(4)、(5)所示：

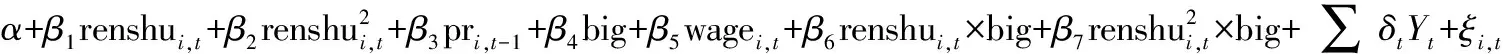
(5)

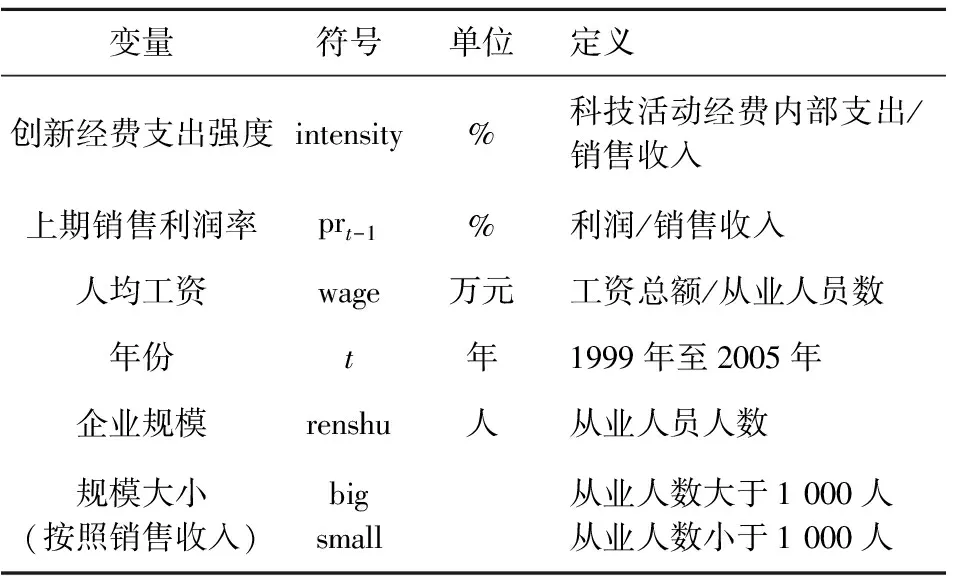
表1 变量定义

3.数据来源与统计描述

本文采用的数据是上海市1998年至2005年大中型工业企业的8年数据。在样本选取过程中，基于数据的完整性和可靠性原则，我们剔除了部分企业，本文最终选取了1 308家企业的年度数据(混合截面数据)作为研究样本。由于混合截面数据通过从不同时点在一个总体中抽取多个随机样本并混合起来得到，在增加样本容量的同时，也可以获得更为精确的估计值，从而为本文的计量分析提供有利条件。

通过对样本中创新经费支出这一被解释变量的样本数据进行描述性统计分析(见表2)，我们发现该变量明显不具备正态性，JB统计量也大大超过了临界值，这都充分验证了样本数据的非正态性与非对称性。因此，若我们采用OLS估计方法进行回归分析，会使得估计出来的系数出现严重偏误，不利于依据回归结果做进一步分析。因此，我们拟采用分位数回归方法，以求实现更为合理、有效的回归结果。

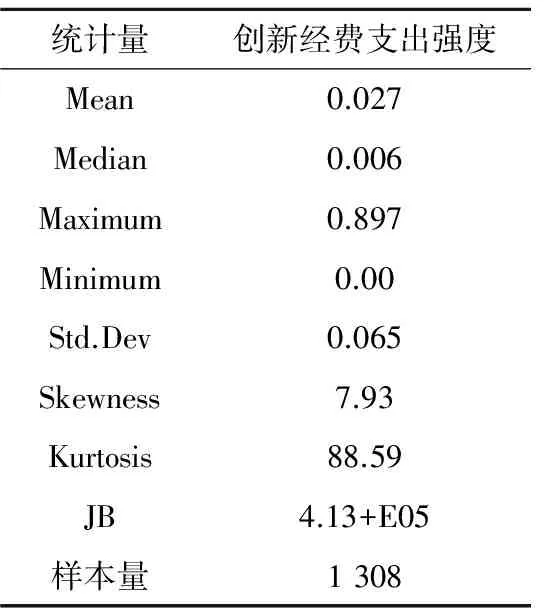
表 2 被解释变量统计描述

四、分析结果与评价

通过运用R软件，我们对所设定的计量模型(5)进行分位数回归，并得到了相应如表3所示的回归估计结果。

(1)从表3结果中可以看出，OLS的回归结果较差，拟合优度极低，且仅有人均工资和企业规模类型分别在5%与1%的水平上显著，多个解释变量显著性较低，这说明由于样本数据的非正态性和非对称性，导致运用OLS方法已经对计量结果带来较大影响。在OLS方法下，企业规模对经费支出强度之间不存在 “U”型或“倒U”关系，大型企业比中型企业创新支出强度要大。但是随着企业人数的增加，两者的表现则大不相同。大型企业规模的增大会导致经费支出强度的下降，而中型企业规模的增大会导致经费支出强度的上升。与此同时，人均工资的上涨会导致投入强度出现较为显著的下降。

表3 分位数回归结果

注：***、**、*分别表示括号内的t统计量在1%、5%、10%的水平上显著

(2)在各个分位点回归结果中，我们发现大型企业较之中型企业，企业创新经费支出强度普遍更高，回归系数均为正值，且随着分位点上升而逐渐增大。其中，在0.5和0.6分位点处系数估计结果最为显著。这说明在创新经费支出强度处在中间位置时，大型企业凭借较为雄厚的资金积累和良好的信用等级，会比中型企业有着更强的创新能力。其中的主要原因在于，大型企业由于具备内部资金集中度高，创新人才实力雄厚，抗研发失败风险能力较强等众多优势，因而在创新经费支出方面力度一般较大。中型企业由于面临扩大企业规模的实际问题，需要从内部资金中拿出部分进行生产规模扩大，以致创新经费支出力度不如大型企业。

图1 不同规模类型企业对经费支出强度影响关系

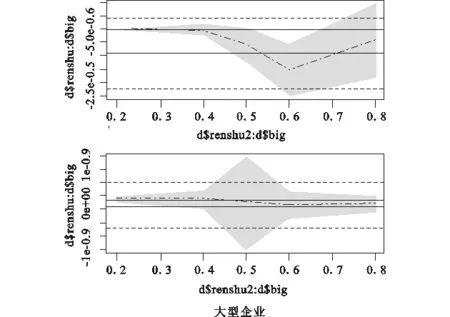
图2 不同类型企业规模与经费支出强度关系

(3)代表企业规模的从业人数在不同规模类型的企业中，也出现了较大差异。中型企业在不同分位点处，一次项和二次项回归系数符号基本为正号——仅在高分位点(0.8)处，二次项系数在1%水平下显著为负数，但是一次项系数显著性较差，总体出现了较不显著的“倒U”型关系。同时，除了在0.8分位点外，在0.2-0.6分位点之间，一次项系数出现了较为显著的上升态势，而二次项系数呈现先增后减的特点。这说明经费支出强度越大，企业人数的增加具有更强的正向作用，但是这种递增的“速度”，在低分位点持续增加，在中高分位点则开始降低。另外一方面，大型企业在各个分位点处出现了截然不同的结果，一次项系数符号始终为负，而二次项系数符号则在中低分位点处(0.2-0.5)为正号，在高分位点(0.6-0.8)处变为负号。因此，结合表3中回归结果，可以发现大型企业在中低分位点(0.2-0.5)处，企业规模与创新经费支出强度之间出现了不同显著强度的“U”型关系。但是，在高分位点处这一关系消失，一次项与二次项系数估计值符号均为负且数值递减。这反映出在经费支出强度的中低分位点处，大型企业的规模变化与支出强度之间并不只是简单的线性关系，企业规模越大，创新支出就越少，但是超过一定临界值后，企业创新研发活动会随着规模的持续增加而加大。然而在高分位点处(0.6-0.8)，大型企业规模的继续扩大，则会对创新经费支出强度带来较大负面影响。其主要原因可能在于，企业规模越大，经营管理层级也会越多，经营决策者的反应速度就会变慢，企业创新意识也更趋保守，而规模过大也会加重企业运营成本，降低决策效率，从而造成对企业研发支出的较大负面影响。

(4)控制变量中，人均工资这一变量在各个分位点上的回归系数符号出现反复，但是仅在低分位点处存在10%水平的显著性。总体而言，在低分位点系数为正，而在中高分位点则为负。说明在低分位点处，由于经费支出强度较小，企业往往会通过引进高端技术人才并提供高薪的办法，加大对创新研发的投入，因此人均工资上涨会带动支出强度的提升。然而上升到了高分位点，人力成本的持续上涨使得企业必须加以全面考虑，同时各种财务约束和限制，也使得企业只有通过减少创新支出才能填补企业经营成本的额外开销。从人均工资变量在中高分位点处的回归系数来看，还可以发现系数估计值是逐渐减小的，也说明人力成本对中高分位点的经费支出强度的负面影响也是逐渐增大的。

(5)另外一个控制变量上一期的销售利润率，在各个分位点处系数估计值显著性都很弱，总体则呈现出在中低分位点处系数符号为负，且数值递减，而在高分位点处符号为正，且数值递增的态势。虽然估计值并不显著，但是所出现的这种现象也值得继续深入分析。我们认为原因在于创新活动本身具备高风险特质，研发支出强度较小的企业，可能对创新研发的风险较为敏感，因此往往采取“尝试性”的研发策略。这类企业一旦获得了丰厚利润，便会在下期将资金进行实物资产投入，导致R&D支出动力不足。另外的原因则可能在于上期利润率的上升会导致企业为了继续保持利润率增长的态势，在研发支出方面采取保守策略，而在下一期降低投入强度。另外一方面，创新经费支出强度较大的企业，往往是创新性技术企业，其经营管理者大都具备很强的创新意识，本身对创新研发就极为重视，而企业本身可能也已经实现了通过技术创新等活动来增强盈利能力的目标，在盈利与创新之间形成了较好的良性循环，因此利润率的上升会加大创新经费的支出总额。

(6)从时间维度来看，2001年与2003年的系数估计值在各个分位点上均不显著,2000年估计值仅在0.4分位点处出现10%的显著性。2002年系数估计值仅在低分位点(0.2)处显著性较低，在其余分位点处均出现了不同程度的显著性正相关关系，这主要是因为2002年上海市人大修改通过了《上海市鼓励引进技术的吸收与创新规定》，有力地促进了企业的各项创新活动。

除了0.9分位点外，在其余分位点上，随着时间的推移，企业均会增加研发投入支出。其中，在2002与2004年，除0.1、0.4、0.8与0.9分位点外，其余分位点均较为显著。而在2004年中小企业板在深圳交易所推出，这些相关支持、鼓励企业创新政策的出台，激发了企业创新的热情，降低了外部融资的交易成本，税负的减少也减轻了企业的负担，企业创新活动的抗风险能力也得到加强。

五、主要结论

本文运用分位数回归模型，对企业规模与企业研发支出强度之间的关系进行了分析与研究，实证分析主要结果如下：

(1)在各个分位点回归结果中，笔者发现大型企业较之中型企业，企业创新经费支出强度普遍更高。回归估计系数均为正值，并随着分位点上升而逐渐增大，且创新经费支出处在中间强度时，大型企业的优势更为显著。

(2)代表企业规模的从业人数系数估计值在不同规模类型的企业中，出现了较大差异，对企业创新经费支出强度的作用出现截然相反的两种情况。中型企业随着规模上升，研发支出强度持续加大，仅在高分位点处出现了较不显著的“倒U”型关系。与此不同，大型企业在中低分位点处出现了不同显著强度的“U”型关系，而在高分位点处则呈现较不显著的负相关关系。

(3)人均工资的上涨，对于创新支出强度不同的企业，会产生不同的影响作用。企业上期利润率对企业创新支出强度并未有显著作用。同时，某些特定年份，不同支出强度的企业出现差异。

结合本文的实证结果，笔者提出如下建议：

第一，大企业要充分利用其拥有众多高素质创新人才和先进设备，以及融资渠道畅通，具有较强信贷能力等优势，发挥创新方面的示范效应，营造良好的创新格局。

第二，中型企业要发挥其管理层创新意识相对更强，经营机制更为灵活，组织结构更为高效的特点，努力实现通过创新取得良好收益绩效的目标。

第三，不同类型企业都要根据自身规模和研发支出强度实际情况，结合企业发展战略目标，在企业内部做好人力、物力、财力的合理配置。同时，充分利用国家技术创新政策，充分发挥出自身的规模经济效应。

需要特别指出的是：由于数据可得性的原因，有些可能会对企业创新支出强度有很好解释关系的变量未能加入模型中，这也在一定程度上减弱了模型的解释能力，因此，采用何种方法更好地得到回归结果是笔者下一步有待研究解决的问题。此外，在采用分位数回归研究中，如何将面板数据模型检验和分位数回归方法结合起来，或采用无条件分位数的方法进行研究，也是下一步需要着重解决的问题。

[1] Scherer.Using Linked Patent and R&D Data to Measure Interindustry Technology Flows[J].The American Economic Review,1965(5):1097-1125.

[2] Schere.On the nature and function of emotion:A component process approach.Approaches to emotion[M].London:Psychology Press,1984:293-318.

[3] Cohen,Levin.Empirical Studies of Innovation and Market Structure[J].Handbook of Industrial Organization,1989(2):1059-1107.

[4] Cohen,Klepper.The Tradeoff between Firm Size and Diversity in the Pursuit of Technological Progress[J].Small business economics,1992(1):1-14.

[5] Cohen,Klepper.A Reprise of Size and R&D[J].The Economic Journal,1996(106):925-951.

[6] Kumar,Saqib.Firm Size,Opportunities for Adaptation,and In-house R&D Activity in Developing Countries:The Case of Indian Manufacturing[J].Research Policy,1996(5):712-722.

[7] Takehiko,Yasuda.Firm growth,size,age and behavior in Japanese manufacturing[J].Small Business Economics,2005,24(1):1-15.

[8] 紫俊武，万迪昉.企业规模与R&D投入强度关系的实证分析[J].科学学研究，2003(1)：58-62.

[9] 朱恒鹏.企业规模、市场力量与民营企业创新行为[J].世界经济，2006(12):41-52.

[10] 安同良,施浩,Alcorta.中国制造业企业R&D行为模式的观测与实证——基于江苏省制造业企业问卷调查的实证分析[J].经济研究,2006(2):21-30.

[11] 罗绍德,刘春.企业R&D投入活动的影响因素分析——基于企业财务资源观[J].财经理论与实践,2009(1):56-60.

[12] 孙晓华,田晓芳.企业规模、市场结构与创新能力——来自中国37个工业行业的经验证据[J].大连理工大学学报:社会科学版,2009(2):29-33.

[13] 刘小元,李永壮.董事会、资源约束与创新环境影响下的创业企业研发强度——来自创业板企业的证据[J].软科学,2009(6):99-104.

[14] 熊彼特.经济发展理[M].北京:商务印书馆,1990.

[15] 熊彼特.资本主义、社会主义与民主[M].北京:商务印书馆,1999.

[16] 加尔布雷斯.美国资本主义:抗衡力量的概念[M].北京:华夏出版社,2008.

[17] Kraft.Market Structure,Firm Characteristics and Innovative Activity[J].The Journal of Industrial Economics,1998(3):329-336.

[18] Koenker and Bassett.Regression Quantiles[J].Econometrica,1978(46):33-50.

[19] Koenker R.Quantile regression for Longitudinal Data[J].Journal of Multivariate Analysis,2004(91):74-89.

[20] 朱平芳,徐伟民.政府的科技激励政策对大中型工业企业R&D投入及其专利产出的影响——上海市的实证研究[J].经济研究,2003(6):45-53.