基于空簧气动响应的高速列车交会动力学分析

， ， ， ，

(1.西南交通大学 机械工程学院，四川 成都 610031；2. 南车青岛四方股份 国家工程实验室，山东 青岛 266111)

随着高速动车组速度的提高，列车空气动力学对车辆运行安全性和平稳性的影响也越来越大。目前，国内外多位学者基于有限体积法对列车空气动力学进行了深入的研究，其研究结果表明[1-4]，列车高速交会时产生的空气动力效应在车辆系统动力学分析中是一个不容忽视的因素。由于高速动车组二系悬挂系统大部分采用空气弹簧，而空气弹簧是一个非线性的气动装置[5-6],虽然一些研究结合列车空气动力学对车辆的动态响应进行了分析[7-8]，但其并未考虑空气弹簧的气动特性。在该研究中，基于空气弹簧的气动流体力学模型和车辆多体动力学模型，首先对动车组高速交会时外部流场变化引起的空气弹簧气动响应进行了分析，其次研究了动车组整车的动力学性能，以期对列车高速交会时车辆运行安全性评估起到一定的借鉴作用。

1 计算模型与气动激励

为了分析动车组在高速交会时的动力学特性，首先建立了某型动车组的整车动力学模型。在该模型中，考虑了空气弹簧的气动流体力学特性；抗蛇行减震器考虑成非线性力元；轮轨间的蠕滑力采用Kalker简化理论(FASTSIM)进行计算；轨道激励选取京津城际高铁轨道谱；整车模型视为多刚体系统，共42个自由度；每个刚体的动力学计算方程如下

(1)

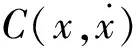
图1 车体与二系悬挂系统示意

由于在会车时，外界流场变化直接作用于车体侧墙，并对空气弹簧的内部压力产生影响，因此需要详细建立车体与二系悬挂系统的动力学方程。假设某型动车组与右侧驶来的同型动车组等速交会，则车体与二系悬挂系统在会车流场下的受力如图1所示。图1中，y、z分别为横向和垂向坐标轴；θ为车体的侧滚角，rad；Mc为车体质量，kg；D为转向架两侧空气弹簧的横向跨距，m；Pv为外界气动流场压力，Pa，可由列车空气动力学计算得到。

车体右墙受到的横向气动压力Fy为

Fy=PvSc

(2)

式中，Sc为车体侧墙的面积。

空气弹簧是一个气动装置，其内部压力会受到列车交会时气动流场变化的影响。若忽略交会流场对左侧空气弹簧的影响，则转向架左右两侧空气弹簧对车体的支撑力FL,R分别为

FL=PiLAeL

(3)

FR=(PiR-Pv)AeR

(4)

式中，L,R分别表示转向架左右两侧；Pi为空气弹簧内部压力；Ae为空气弹簧有效面积。

对于车体，考虑其横摆、沉浮和侧滚三个自由度，并忽略空气弹簧垂向与横向刚度的耦合作用，则可根据式(1)列出其动力学方程为

(5)

式中，Ixx为车体的侧滚转动惯量；Y,Z分别为车体质心的横向与垂向位移；Cy为二系横向减震器的阻尼；h为车体质心距空簧上表面的垂向高度；Ky为空气弹簧的横向刚度；Kθ为抗侧滚扭杆的抗侧滚刚度；g为重力加速度。

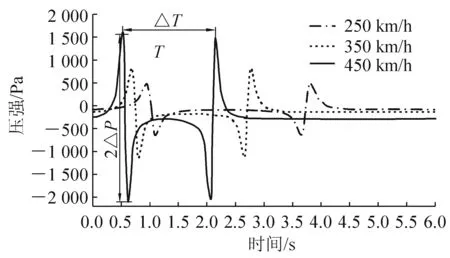
图2 会车气动流场压力的时间历程

由式(5)可知，车体的横向气动压力Fy与右侧空气弹簧对车体的支撑力FR均与会车流场压力Pv有关。在车辆动力学计算中，选取列车中部右墙侧窗下的点作为观测点，由于该点在会车气动流场中的压力变化具有代表性，可假设车体右墙在垂直方向上受到的压力与观测点相等，如图1所示。根据文献[2-3,8]对列车空气动力学的研究结果，在交会列车车头鼻端通过观测点之前，其周围流场为压缩波，观测点压力增加；车头鼻端通过观测点后，其周围流场为膨胀波，观测点压力减小；车尾鼻端通过观测点时流场变化历程与之相反。这样，某型动车组中部右墙侧窗下观测点压力变化的时间历程如图2所示。图2中，ΔP为会车压力波幅值；ΔT为交会列车通过观测点的时间。根据文献[3]，列车等速交会时观测点压力波幅值ΔP的拟合公式为

ΔP=0.132 5V2

(6)

式中，V为车速。此外，ΔT按照下式计算

ΔT=L/(2V)

(7)

式中，L为整列车长度。这样，会车气动流场压力Pv随时间t的变化历程可表示为压力波幅值ΔP与交会通过时间ΔT的函数

Pv=Pv(ΔP,ΔT,t)

(8)

在数值计算中，选取的某型动车组整列车长度为406 m。经计算，两列该型动车组分别以250 km/h、350 km/h、450 km/h等速度会车时，会车流场压力Pv的时间历程如图2所示，ΔP与ΔT的大小列于表1。在下面的研究中，将以Pv的时间历程作为外界激励，对空气弹簧的响应以及车辆的动力学性能进行分析。

2 空气弹簧的气动响应

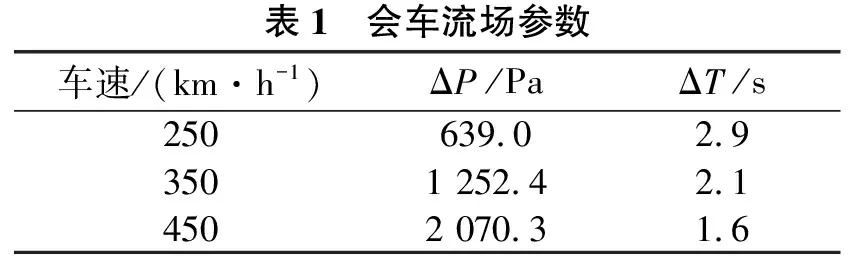
表1 会车流场参数车速/(km·h-1)ΔP/PaΔT/s250639.02.93501 252.42.14502 070.31.6

空气弹簧是一个气动装置，对外界环境参数变化较敏感。因此，需要基于AMESim仿真平台建立空气弹簧的气动流体力学模型。在该模型中，考虑了空气弹簧内部气体的热力学过程以及有效面积与内部压力的函数关系；由于应急橡胶弹簧的刚度远大于橡胶气囊的刚度，因此在空气弹簧的正常工作状态中不考虑应急橡胶弹簧的刚度。此外，基于SIMPACK建立车辆多体动力学模型，并将其与AMESim中的空气弹簧气动流体力学模型相结合，以空气弹簧的支反力作为车辆动力学计算的输入，以车体的垂向位移作为输出，其联合仿真示意图如图3所示。在列车交会的动力学分析中，以会车流场压力Pv的时间历程作为输入，通过联合仿真分别计算两列动车组以250 km/h、350 km/h、450 km/h的速度在直线上等速交会时空气弹簧的气动响应以及动车组的动力学响应。

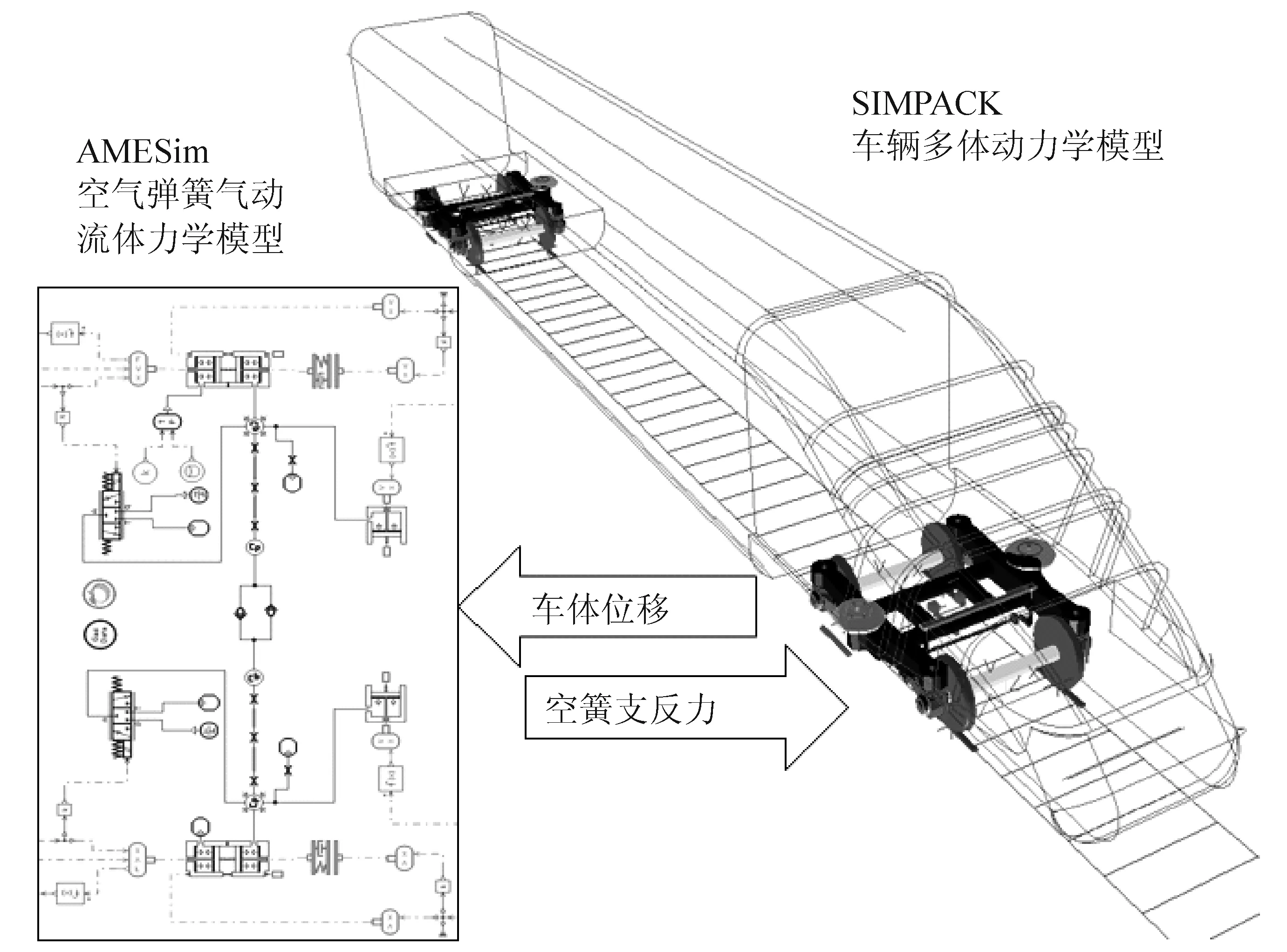
图3 车辆多体动力学模型与空气弹簧气动流体力学模型联合仿真示意图

空气弹簧的动刚度与其内部压力有很大的关系，在研究动车组整车动力学性能前，首先需要研究空气弹簧在列车交会时的气动响应。空气弹簧外界气压的变化采用式(8)中Pv时间历程作为输入。在不同的车速工况下进行数值计算，得到某型动车组前转向架左、右两侧空气弹簧的内压变化分别如图3、图4所示。

将图4、图5与图2进行对比后可以看出，左侧空气弹簧内压变化与会车流场气压变化一致，而右侧空气弹簧内压变化与会车流场气压变化相反。这是由于当车体右侧压力增加时，气动力会对车体产生逆时针的力矩作用，虽然右侧空气弹簧的外压有所增加，但是远小于车体逆时针侧滚对左侧空气弹簧产生的压力增加。因此，当右侧会车流场压力增加后，左侧空簧内压增加而右侧空簧内压减小，反之亦然。后转向架空气弹簧内压变化规律与前转向架相似，在此不再赘述。

图4 前转向架左侧空簧内压变化 图5 前转向架右侧空簧内压变化

将不同车速下各个位置空气弹簧内压的最大值与最小值列于表2，并计算出每种工况下空气弹簧内压的最大波动。由表2中的计算结果可知，交会车速越高，空气弹簧的内压波动越大，当两列动车组以450 km/h的车速交会时，空气弹簧的内压波动可以达到30.73%。而空气弹簧的内部压力会直接影响空气弹簧的动态特性[5-6]，因此需要基于空气弹簧的气动响应深入分析动车组在交会时的整车动力学特性，并对其运行安全性进行评判。

表2 不同车速下各空气弹簧内压最值比较车速/(km·h-1)前左空簧内压/kPa最大值最小值前右空簧内压/kPa最大值最小值后左空簧内压/kPa最大值最小值后右空簧内压/kPa最大值最小值最大波动/%250620.8 523.4 623.6 526.7 631.0 523.8 634.3 522.8 19.27350633.7 510.0 630.0 517.6 632.6 511.3 642.2 519.4 21.63450670.2 497.3 656.1 485.0 660.7 484.7 656.8 495.3 30.73

3 动车组交会时整车动力学分析

由于车体受到会车气动流场的直接作用，且支撑车体的空气弹簧对压力变化较为敏感，因此需要首先研究车体在会车过程中的动态响应。车体的侧滚角θ与横移量Y在会车过程中的响应曲线分别如图6和图7所示。观察图6可知，车体侧滚角的变化趋势与会车流场压力的变化趋势相反，即当车体右侧流场压力增加时，车体发生逆时针侧滚运动，同时导致了转向架左侧空气弹簧内压升高，而右侧空气弹簧内压下降。由图7可知，交会车速越高，车体横移量越大；车体在交会初始正压力波的推动下首先向左侧横移，此后压力波出现两个负峰值点，车体受吸引作用向右侧横移，最后在车尾通过观测点时正压力波的作用下，车体又逐渐回复至平衡位置。

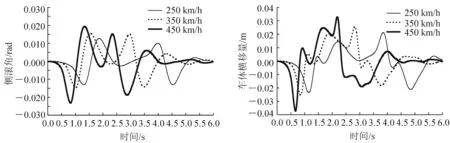
图6 车体侧滚角的动态响应 图7 车体横移量的动态响应

车体在会车过程中的振动响应会直接影响动车组的运行平稳性。车辆运行平稳性指标W可根据下式进行计算[9]

(9)

式中，A为车体的振动加速度；f为车体的振动频率；F(f)为与振动频率有关的修正系数，详见文献[9]。经过计算，将不同车速交会下的车辆运行横向与垂向平稳性指标列于表3。由计算结果可知，在各种工况下的车辆横向平稳性指标均大于垂向平稳性指标，说明车体的横向振动受到会车流场的影响较垂向振动更大。

车体在列车交会过程中的振动响应会通过一系、二系悬挂系统传递至轮轨，影响车辆的运行安全性。根据《铁道车辆动力学性能评定和试验鉴定规范》[9]，车辆运行安全性指标包括轮轨垂向力、轮轴横向力、脱轨系数以及轮重减载率。

表3 车辆运行平稳性计算结果车速/(km·h-1)垂向平稳性横向平稳性2502.1332.7563502.2003.1074502.2653.446

根据规范要求，对于算例中选取的某型动车组而言，轮轨垂向力的限值为170 kN；轮轴横向力的限值为56.26 kN；脱轨系数的限值为0.8；轮重减载率的限值为0.8。在不同会车车速工况下进行数值仿真，得到车辆的动力学响应，选取每种工况下动力学性能最差的轮对响应曲线，将其与安全性限值绘于图8中。

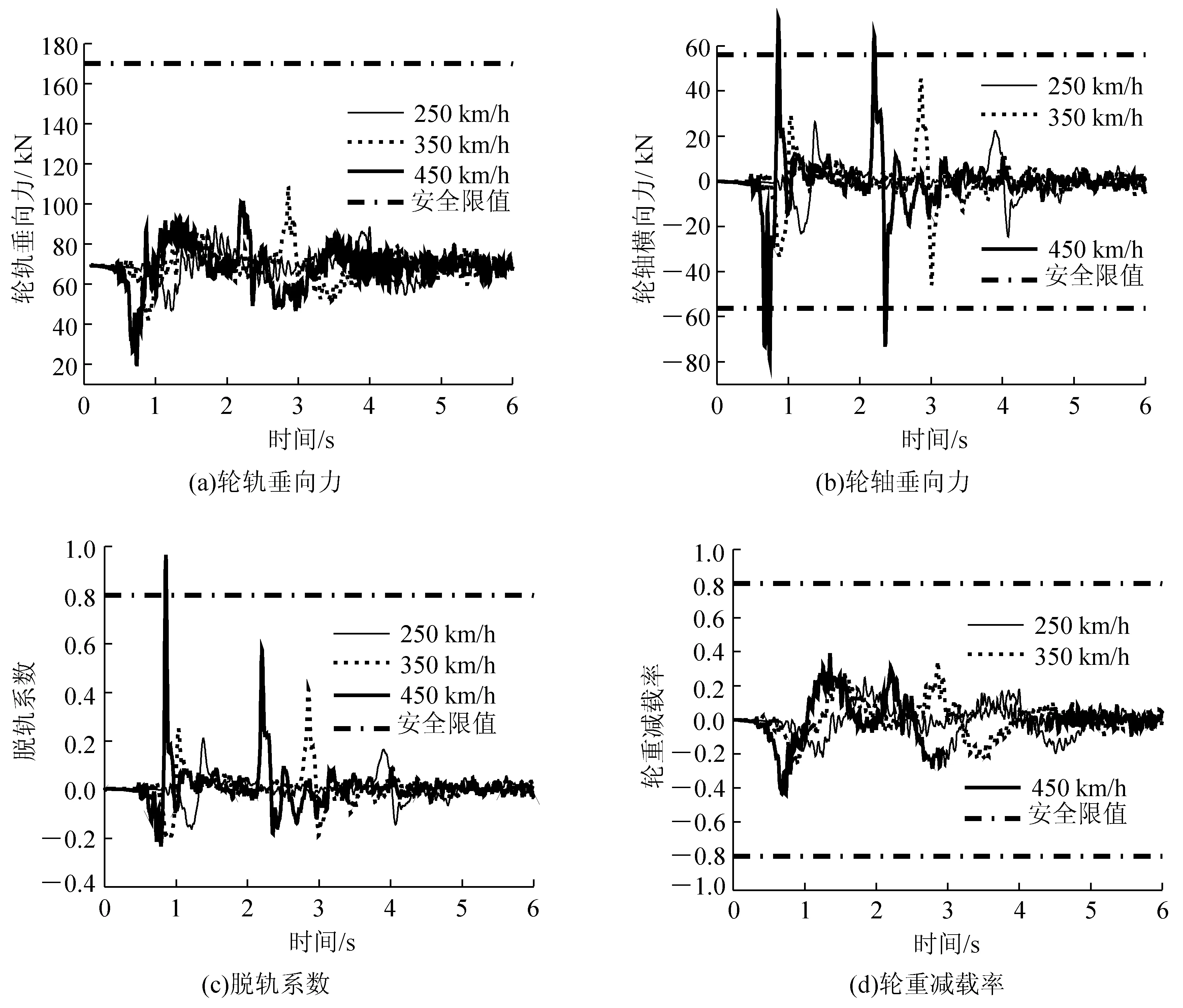
图8 会车过程的车辆动力学响应

根据车辆在会车过程中的响应曲线可知，在几项安全性指标中，轮轨垂向力与轮重减载率在会车过程中有较大的安全余量；而轮轴横向力和脱轨系数在450 km/h工况下会在短暂的时间中超过安全限值。这是由于会车气动流场对车体的横向作用力较大，主要影响与轮轨横向力有关的安全性指标。通过观察轮轴横向力和脱轨系数超过安全限值的峰值点可知，运行安全性指标的危险点一般出现在交会列车前部鼻端通过观测点的时刻，故应在高速列车的鼻端设计中设法降低会车时的初始压力波幅度，以提高动车组在高速会车时的运行安全性。

4 结论

基于列车空气动力学的研究成果，以列车交会流场的气压变化作为外部激励，并将车辆多体动力学模型与空气弹簧的气动流体力学模型相结合进行数值计算，研究了两列动车组以不同的车速交会时空气弹簧的气动响应以及车辆的动力学响应，并得到了以下一些主要结论：

(1)当动车组与相向驶来的列车交会时，由会车压力波变化所造成的空气弹簧压力波动远小于车体侧滚造成的压力波动，因此空气弹簧的内压变化主要受车体侧滚的影响，转向架靠近会车侧空气弹簧内压的变化趋势与会车气动流场的变化趋势相反，转向架另一侧空气弹簧内压的变化趋势与之相同。

(2)动车组交会速度越高，空气弹簧内压变化幅度越大，当交会车速为450 km/h时，空气弹簧内压的最大波动可达到30.78%。

(3)车体横向振动较垂向振动受会车气动流场的影响更大，且在各车速交会工况下，车辆的垂向平稳性均优于横向平稳性。

(4)轮轨垂向力与轮重减载率受会车气动流场的影响较小，这两项安全性指标在会车过程中仍有较大的安全余量，但轮轴横向力与脱轨系数在450 km/h的工况下会在短暂的时间中超过安全限值，且这两项安全性指标的最大值均出现在车头鼻端通过观测点的时刻。

参 考 文 献

[1]H Hemida,Baker C.Large-eddy simulation of the flow around a freight wagon subjected to a crosswind [J]. Computers and Fluids, 2010, 39(10): 1944-1956.

[2]Hwang J,Yoon T S,Lee S G.Numerical study of unsteady flowfield around high speed trains passing by each other[J]. JSME International Journal, Series B: Fluids and Thermal Engineering, 2001, 44(3): 451-464.

[3]田红旗，许平，梁习锋,等.列车交会压力波与运行速度的关系[J]. 中国铁道科学, 2006, 27(6): 64-67.

[4]李人宪，赵晶，刘杰,等.高速列车会车压力波对侧窗的影响[J].机械工程学报, 2010, 46(4): 87-92, 98.

[5]李芾,付茂海,黄运华.空气弹簧动力学特性参数分析[J].西南交通大学学报,2003,38(3):276-281.

[6]Homeyer A,Maβmann C.Moderne verfahren zur auslegung von luftfedersystemen[J]. ZEV+DET Glas, 1998, 122(9/10): 549-554.

[7]张新, 李向国, 王海云,等.轨距不平顺激励下高速列车动力响应研究[J]. 石家庄铁道大学学报：自然科学版, 2011,24(1): 69-72,77.

[8]Yasushi T,Yasuhiko I,Seiji Y,et al. Evaluation method for air pressure variation and station facility member deterioration caused by high-speed train passage in stations[J].Quarterly Report of RTRI (Japan), 2008, 49(2): 89-95.

[9]铁道部标准计量研究所.GB5599—85 铁道车辆动力学性能评定和试验鉴定规范[S].北京:中国标准出版社,2008.