铁路钢-混凝土结合梁动力响应试验研究
, 运生,
(1.石家庄铁道大学 土木工程学院,河北 石家庄 050043;2.清华大学 土木工程系,北京 100084)
近些年,随着中国经济的高速发展,为了满足运输需求,铁路建设步入了高速发展阶段。而钢-混凝土结合梁桥凭借其自重轻、噪音小、便于施工以及能充分发挥钢材和混凝土材料各自特性等优点已逐步在桥梁建设中占据一席之地。
随着结合梁桥的广泛应用,许多学者已从试验和理论方面对其静力性能进行了深入的研究[1-6],形成了较为完善的体系,然而随着列车提速、货车载重逐步增加和交通流量的显著加大,使结合梁桥的车桥振动加剧,动力响应问题日渐突出,但有关结合梁桥动力性能方面的研究还相对较少。蒋丽忠、丁发兴 等[7]对某客运专线的钢-混凝土连续结合梁桥进行了动力性能试验,测试了高速列车下结合梁桥的动力响应,根据实测数据综合评价了铁路桥体系的各种性能;郑则群、房贞政[8]对3跨钢-混凝土组合连续梁桥进行了环境激励及汽车动载激励试验,分析了不同参数对结合梁自振频率的影响;Khaled M. Sennah et al[9]通过建立的有限元模型对单室和多室曲线公路结合梁在汽车荷载作用下的冲击系数进行了研究;K. Liu[10]采用ANSYS软件建立了车桥有限元模型,从理论上对铁路结合梁在列车荷载作用下的动力系数进行了分析。以上学者多运用数值模拟方法对结合梁桥的动力特性进行了研究,虽然也有部分研究进行了现场实测,但限于现场条件,无法对试验参数进行灵活的变化。
为了对结合梁的动力性能有更深入的研究,设计了6片钢-混凝土简支结合梁,通过变化模型列车的载重和速度,测试了结合梁模型在移动荷载作用下的动力响应,并根据试验结果对结合梁动力响应的变化规律进行了分析。
1 试验概况
1.1 车桥模型简介
本试验中6片试验梁以剪力连接度为分组依据,分为完全连接结合梁(FCB梁组)和部分连接结合梁(PCB梁组),分别进行动力响应的测试。每组试验梁又根据不同的栓钉损伤工况各分为3片梁(FCB、FCB1、FCB2和PCB、PCB1、PCB2),以进行栓钉局部损伤识别的研究,试验梁其它参数均相同。本文只进行动力响应部分的试验研究。
试验梁主要尺寸:总长4 500 mm,简支跨度4 200 mm;混凝土板宽700 mm,厚70 mm;钢梁高200 mm,下翼缘宽400 mm,上翼缘宽60 mm,上、下翼缘板厚8 mm,腹板厚6 mm;所选栓钉直径为13 mm,高50 mm,完全连接结合梁中共布置70个栓钉,不完全连接结合梁中共布置42个栓钉,连接度为60%;钢梁均采用Q235钢,混凝土C30。各试验梁截面尺寸见图1。

图1 结合梁布置图(单位:mm)
试验中在试验梁表面铺设了1∶10仿真轨道(见图2),并采用1∶10缩尺C70敞车模型作为试验车辆,主要尺寸:总长1 397.6 mm、车辆宽度324.2 mm、车辆高度314.3 mm、固定轴距183 mm、车辆空载时为62 kg。试验车辆见图3。

图2 试验梁及轨道 图3 试验车辆
1.2 试验测试项目和试验装置
(1)跨中加速度:采用东方所941B竖向拾振器。为测试行车过程中试验梁跨中加速度时程,在试验梁跨中混凝土板顶面布置竖向传感器,并通过微型拨动开关选择加速度档。
(2)试验梁跨中挠度和支座处结合面滑移:均采用位移计。在梁端支座处布置一个位移计,用来测量支座处结合面滑移,试验梁跨中处布置一个位移计用来测量跨中挠度。
(3)数据采集装置:采用东方所16通道(3018C)采集仪对行车过程中试验梁动力响应时程进行实时监控和数据采集。
1.3 试验工况
试验中对C70型敞车施加不同配重,分别获得62 kg、100 kg和150 kg车重。采用人工推车的方法,使试验车辆速度由低到高分为5~8级变化。为了获得较为准确的车辆行驶速度,本试验中有专门录像人员对车辆运行过程进行实时录像计时。
2 试验梁动力响应测试结果分析
2.1 测试结果
对6片试验梁进行了移动荷载下动力响应的测试,结果显示FCB梁组和PCB梁组各试验梁测试结果规律基本相同,为了避免叙述上的重复,不再对6片试验梁进行一一叙述,只给出不同车重试验车辆以约2 m/s的速度通过FCB梁和PCB梁时的跨中动力响应波形曲线。由于试验中受外界高频波的干扰,对各波形曲线进行80 Hz低频波滤波处理,见图4~图7,其它工况不再一一列出。

图4 FCB梁跨中动挠度曲线

图5 FCB梁跨中加速度曲线

图6 PCB梁跨中动挠度曲线

图7 PCB梁跨中加速度曲线
由图4~图7可知:
(1)随车辆的前移,曲线以波动形式变化且挠度值逐渐增大,当车辆行驶到试验梁跨中附近时跨中挠度值最大,当车辆驶过跨中后,挠度值随之减小并逐渐趋于0;货车质量为62 kg、100 kg和150 kg时,FCB梁跨中最大动挠度分别为0.076 8 mm、0.108 mm和0.165 mm,PCB梁跨中最大动挠度分别为0.076 2 mm、0.115 1 mm和0.176 8 mm,均呈增大趋势。
(2)加速度曲线图中,虚矩形框内均出现了加速度曲线突变的现象,这是由于车辆前后轮分别驶过轨道接头处造成的,虚曲线大致给出了忽略轨道接头影响时加速度曲线的变化趋势。随着车辆的前移,加速度曲线均呈现逐渐减小的趋势,当车辆出桥后,加速度逐渐衰减并回到初始值。从图中还可看出PCB梁与FCB梁相比,车辆前移过程中加速度曲线出现若干较大突变。
由于完全抗剪连接的FCB梁结合面滑移很小,测试精度较差,故本试验仅对部分连接结合梁(PCB梁)进行了钢梁与混凝土板之间结合面的相对滑移测试,图8给出了不同质量试验车辆以2 m/s通过PCB梁时支座位置结合面的滑移时程曲线。

图8 PCB梁支座位置结合面滑移时程曲线
由图8可知,货车质量为100 kg和150 kg时PCB梁最大滑移分别约为1.89×10-3mm、2.56×10-3mm;随着货车在梁上运行,滑移曲线均大致呈波动式上升,货车位于跨中附近时达到最大值,之后滑移曲线逐渐减小,货车出桥时滑移曲线不再降低,从图中可看出最终结合面滑移值均没有恢复到初始零值。
2.2 测试结果分析
2.2.1 速度与梁跨中挠度的关系
为了获得较为准确的车辆行驶速度,本试验采用了波形曲线分析与现场实时录像测试相结合的方法。跨中挠度最大值取自80 Hz低频滤波后曲线。由于试验数据较多且各试验梁规律相同,此处只给出FCB梁、PCB梁跨中最大动挠度与速度的关系,见图9。

图9 速度与跨中挠度关系曲线
从图9可看出,随着行车速度的逐步增大,速度与挠度并非呈线性变化,而是在某些速度点处有下降现象,但总体来说随速度增加挠度呈上升趋势,且货车质量越大引起跨中动挠度值越大。
2.2.2 速度与结合面相对滑移的关系
通过对部分连接结合梁PCB的结合面滑移测试,得到了该试验梁车辆速度与结合面最大滑移值的关系曲线,见图10。
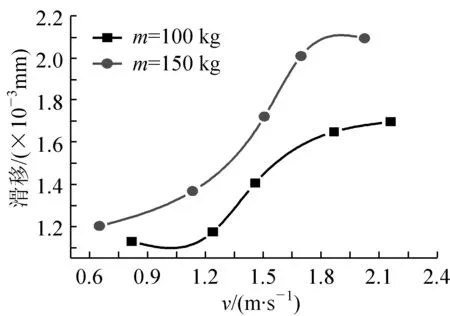
图10 结合面最大滑移与速度关系曲线
由图10可知,随货车质量的增大和行车速度的增加,试验梁结合面相对滑移均呈增大趋势,且行车速度对结合面相对滑移的影响比对跨中挠度的影响更加明显。在不同的车重下,总体规律表现为当速度较小时,相对滑移随行车速度的增加趋势比较平缓;增大到一定速度后,增长幅度加剧,之后又逐渐平缓。这说明支座截面结合面的最大滑移并非随行车速度线性增长,而是在某一速度段内达到最大,具体速度区间应通过对实桥的分析进行确定。
2.2.3 抗剪连接度与梁跨中挠度的关系
为了分析抗剪连接度对试验梁跨中挠度的影响,分别比较了货车质量为100 kg时FCB梁和PCB梁以及FCB1梁和PCB1梁的连接度-最大挠度曲线见图11。

图11 抗剪连接度与模型梁跨中最大挠度关系曲线
由图11可知,部分连接结合梁的跨中最大动挠度要高于完全连接结合梁,这说明随剪力连接度的降低,结合梁刚度下降,柔性增强,从而试验梁的动力响应变大。
2.2.4 行车速度、抗剪连接度与动力系数的关系
列车通过桥梁时,对桥梁产生的动力效应往往会大于其静止作用在桥上所产生的静力效应。这种增大效应通常以动力系数来表示,动力系数[11]。
动力系数=Sdy/Sst
(1)
式中,Sdy为桥梁最大动力响应,Sst为列车在桥上静止时该桥最大静力响应。本试验中以车辆静止时试验梁跨中最大静挠度作为Sst,而列车通过桥梁时得到的结合梁跨中最大动挠度作为Sdy。
图12给出了货车质量为62 kg、100 kg时FCB梁、PCB梁动力系数曲线。

图12 FCB、PCB梁动力系数曲线
由图12可知,随着行车速度的逐步增大,速度与动力系数并非呈线性变化,而是在某些速度点处有下降现象,但总体来说随速度增加动力系数呈上升趋势;当车速较小时,两试验梁动力系数相差不大,当车速较大时,PCB梁动力系数要高于FCB梁。
2.2.5 栓钉损伤与梁跨中挠度的关系
为了分析不同栓钉损伤对试验梁跨中挠度的影响,分别比较了货车质量为100 kg时FCB梁和FCB1梁以及PCB梁、PCB1梁和PCB2梁的损伤-最大挠度曲线见图13。

图13 不同栓钉损伤与模型梁跨中最大挠度关系曲线
由图13可知,FCB梁组和PCB梁组在不同栓钉损伤情况下,跨中动挠度变化规律及其数值大小基本相同,这说明栓钉的局部损伤对结合梁整体动力性能影响不大。
3 结论
对6片钢-混凝土结合梁模型进行了模型列车以不同速度和不同重量通过时的动力测试,得到的主要结论如下:
(1) 随车辆的前移,结合梁跨中挠度曲线以波动式变化且挠度值逐渐增大,当车辆行驶到试验梁跨中附近时跨中挠度值最大;随剪力连接度的减小,部分连接结合梁的刚度降低,在相同车重和车速下,其跨中最大动挠度值要高于完全连接结合梁。
(2) 随着行车速度的逐步增大,行车速度与结合梁跨中最大挠度并非呈线性变化,而是在某些速度点处有下降现象,但总体来说随速度增加挠度呈上升趋势。
(3) 结合面相对滑移随货车质量及车辆速度的增加呈现增大趋势,且最大滑移并非随行车速度线性增长,而是在某一速度段内达到最大。
(4) 动力系数曲线随行车车速的增大总体呈增大趋势,随剪力连接度的降低,结合梁动力系数有增大趋势。
(5) 随剪力连接度的降低,试验梁的动力响应变大;在剪力连接度相同情况下,不同栓钉损伤对结合梁动力性能影响不大。
参 考 文 献
[1]聂建国,熊辉,胡少伟. 开口截面钢-混凝土结合梁弯扭性能的理论分析及试验研究[J]. 土木工程学报, 2004, 37(11): 6-10.
[2]聂建国,唐亮,胡少伟. 钢-混凝土组合箱梁的抗扭强度[J]. 土木工程学报, 2008,41(1): 1-11.
[3]许伟,许峰,林长宇,等.钢与高强混凝土连续结合梁非线性分析[J].沈阳建筑大学学报:自然科学版,2010,26(4):695-698.
[4]石启印,马波,李爱群. 外包钢-混凝土结合梁的试验研究和理论分析[J]. 建筑结构,2006,36(8):60-63.
[5] Cas B, Bratina S, Saje M, et al. Nonlinear analysis of composite steel-concrete beams with incomplete interaction [J ]. Steel and Composite Structures, 2004, 4(6):489-507.
[6]Queiroz F D, Vellasco P C, Nethercot D A. Finite element modeling of composite beams with full and partial shear connection[J]. Journal of Constructional Steel Research,2007,63(4):505-521.
[7]蒋丽忠,丁发兴,余志武. 钢-混凝土连续组合铁路桥梁综合动力性能试验研究[J]. 中国铁道科学,2006, 27(5): 60-65.
[8]郑则群,房贞政.钢-混凝土组合连续梁桥动力响应试验研究[J].地震工程与工程振动,2006,26(4):175-181.
[9]Khaled M,Sennah, ASCE M, et al. Impact factors for horizontally curved composite box girder bridges[J].Journal of Bridge Engineering, 2004,9(6):512-515.
[10]Liu K, Roeck G De , Lombaert G. The effect of dynamic train-bridge interaction on the bridge response during a train passage[J]. Journal of Sound and Vibration, 2009, 325: 240-251.
[11]EN. Eurocode-Basis of structural design, Final Draft, European Committee for standardization[S].CEN: European Committee for Standardization, 2006.

