斜拉桥结构模型试验索力测试方法研究

,

(石家庄铁道大学 工程力学系,河北 石家庄 050043)

桥梁模型试验是解决桥梁工程科研和设计中出现的新问题时不可缺少的手段，也是对桥梁结构进行损伤识别研究的重要手段之一。斜拉桥结构由于其跨越能力大，造型美观等特点，得到了越来越多的应用。对斜拉桥结构的模型试验研究也越来越多[1-7]。斜拉索作为斜拉桥结构重要的受力构件，其索力的测试一直是关注的重点和热点问题。对斜拉桥结构模型试验中的索力测试研究目前上不够深入。文献[1-2]中斜拉索索力测试采用将测力装置串联在斜拉索中进行，文献[3]则采用在斜拉索上粘帖应变片的方式进行索力测试；文献[4]中斜拉索由上、下锚件、中间连接段、测力装置和索力调整装置串联而成。这些索力测试方法在模型试验中均存在一定的局限性，如索力测试采用串联测力装置在拉索中，由于须将拉索断开，对拉索的刚度造成了一定程度的改变，也影响了拉索的整体受力性能，而在拉索上粘帖应变片的方式则质量难以保证，不能长期进行监测。

结合一座独塔斜拉桥试验模型，对斜拉桥模型试验中的索力测试方法展开研究，创新的将压力环传感器引入到模型试验的索力测试中，对索力测试系统进行了系统的设计和仿真分析，并将理论分析结果与试验结果进行了对比分析，实现了拉索索力的方便、快捷、准确、长期测试。

图1 试验模型布置

1 试验模型简介

试验模型跨度为2.6 m+2.6 m，主梁选用铝合金材料，箱型截面，分节段栓接而成；主塔选用I字钢，杠杆加载系统由门架、杠杆组织和过梁系统三部分组成。斜拉索全桥共9组，每组4根，共计36根，选用高强钢丝。试验模型如图1所示。

2 斜拉索索力测试系统

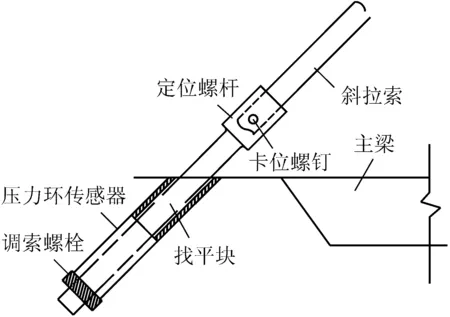
图2 索力测试系统

索力测试系统主要有定位螺杆、找平块、压力环传感器、调节螺栓等构件组成，安装在索梁锚固区。将压力环传感器与测试仪器用导线连接，可以实时、快捷的对斜拉索索力进行测量。索力测试系统构造如图2所示。

2.1 压力环传感器的制作

为节约试验成本，本次试验压力环传感器传感原件主要采用电阻应变片，根据电阻应变片的测试灵敏度，压力环材料选用铝合金圆环，外径13 mm，壁厚2.5 mm。制作过程相对简单，将电阻应变片粘贴于压力环表面，为消除偏心影响，每个压力环上粘贴2个电阻应变片，外用防水胶带保护。本模型共计36根斜拉索，每个拉索下均设置一个压力环传感器，共计36个。

2.2 索力测试系统仿真

数值仿真基于Ansys分析平台进行，建立压力环传感器测力系统的有限元分析模型。根据图2所示，压力环与找平块以及压力环与调索螺栓之间均为挤压接触连接，因此应按接触问题进行仿真。

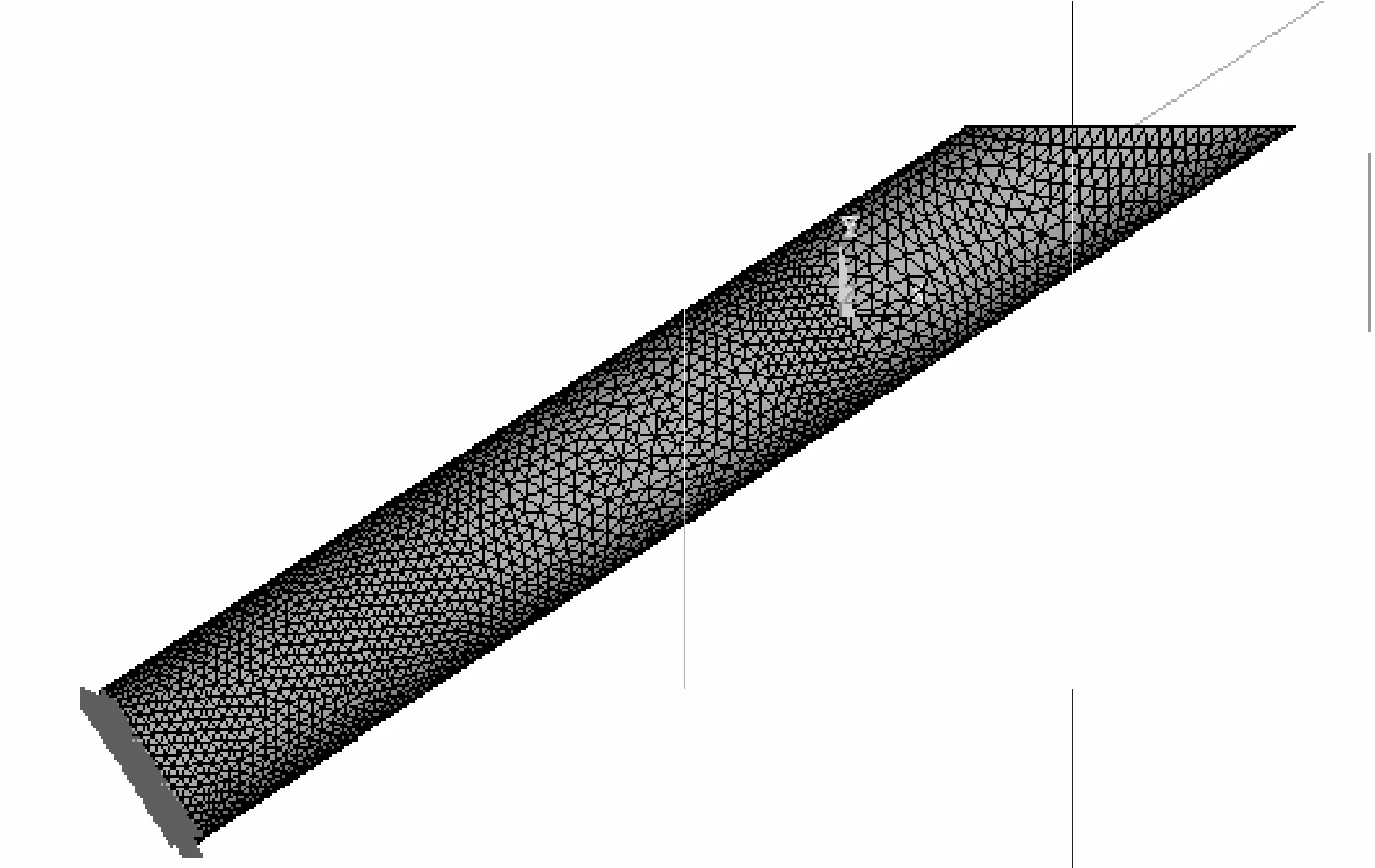
图3 压力环有限元分析模型

接触问题实质上是一种高度非线性行为，可以分成两种基本类型：刚体—柔体接触和柔体—柔体接触。本文中由于压力环的材料弹模远小于找平块材料以及调索螺栓材料，因此简略认为是刚—柔接触问题。系统包括两个接触对，一为压力环与找平块，一为压力环与调索螺栓。选择压力环的上下面为接触面，选择找平块、调索螺栓与压力环接触的面为目标面。接触面选用Conta174单元(三维8节点面面接触单元)模拟，目标面选用Targe170单元(三维8节点目标面单元)模拟。压力环采用SOLID187单元模拟，拉索采用LINK10单元模拟。考虑到索力测试系统锚固与主梁下方，拉索与主塔连接，而主梁、主塔的刚度均较大，但单根调索时引起主梁、主塔的变形很小，因此近似认为找平块与主梁接触面为固结，拉索上端为固结。由此建立的有限元分析模型如图3所示。

仿真分析中主要讨论了压力环角度、斜拉索长度以及斜拉索索力改变时压力环传感器的应变变化情况。具体仿真分析结果如表1、表2及表3所示。

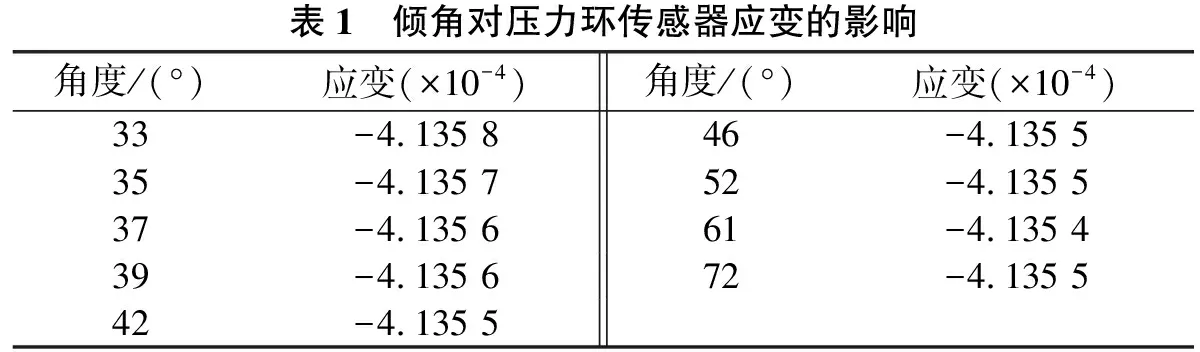
表1 倾角对压力环传感器应变的影响角度/(°)应变(×10-4)角度/(°)应变(×10-4)33-4.135 846-4.135 535-4.135 752-4.135 537-4.135 661-4.135 439-4.135 672-4.135 542-4.135 5

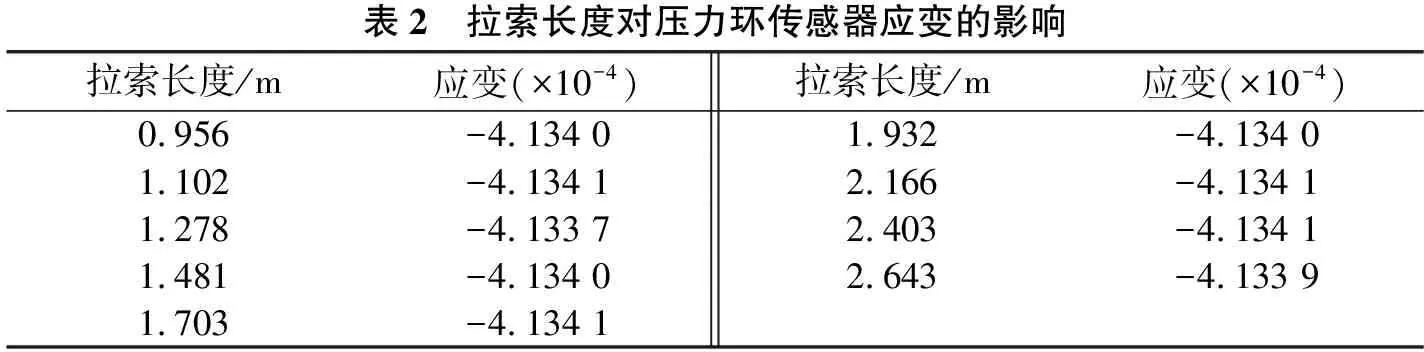
表2 拉索长度对压力环传感器应变的影响拉索长度/m应变(×10-4)拉索长度/m应变(×10-4)0.956-4.134 01.932-4.134 01.102-4.134 12.166-4.134 11.278-4.133 72.403-4.134 11.481-4.134 02.643-4.133 91.703-4.134 1

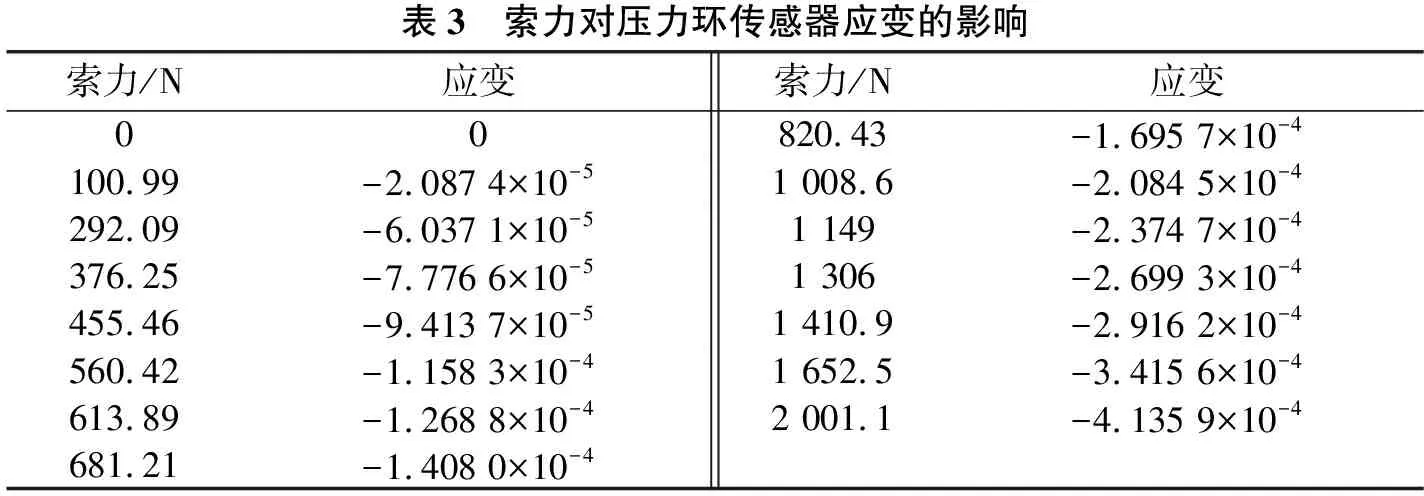
表3 索力对压力环传感器应变的影响索力/N应变索力/N应变00820.43-1.695 7×10-4100.99-2.087 4×10-51 008.6-2.084 5×10-4292.09-6.037 1×10-51 149-2.374 7×10-4376.25-7.776 6×10-51 306-2.699 3×10-4455.46-9.413 7×10-51 410.9-2.916 2×10-4560.42-1.158 3×10-41 652.5-3.415 6×10-4613.89-1.268 8×10-42 001.1-4.135 9×10-4681.21-1.408 0×10-4

表1～表3中的应变值为压力环中部5 mm长度应变的平均值，主要是为消除应力集中等影响。

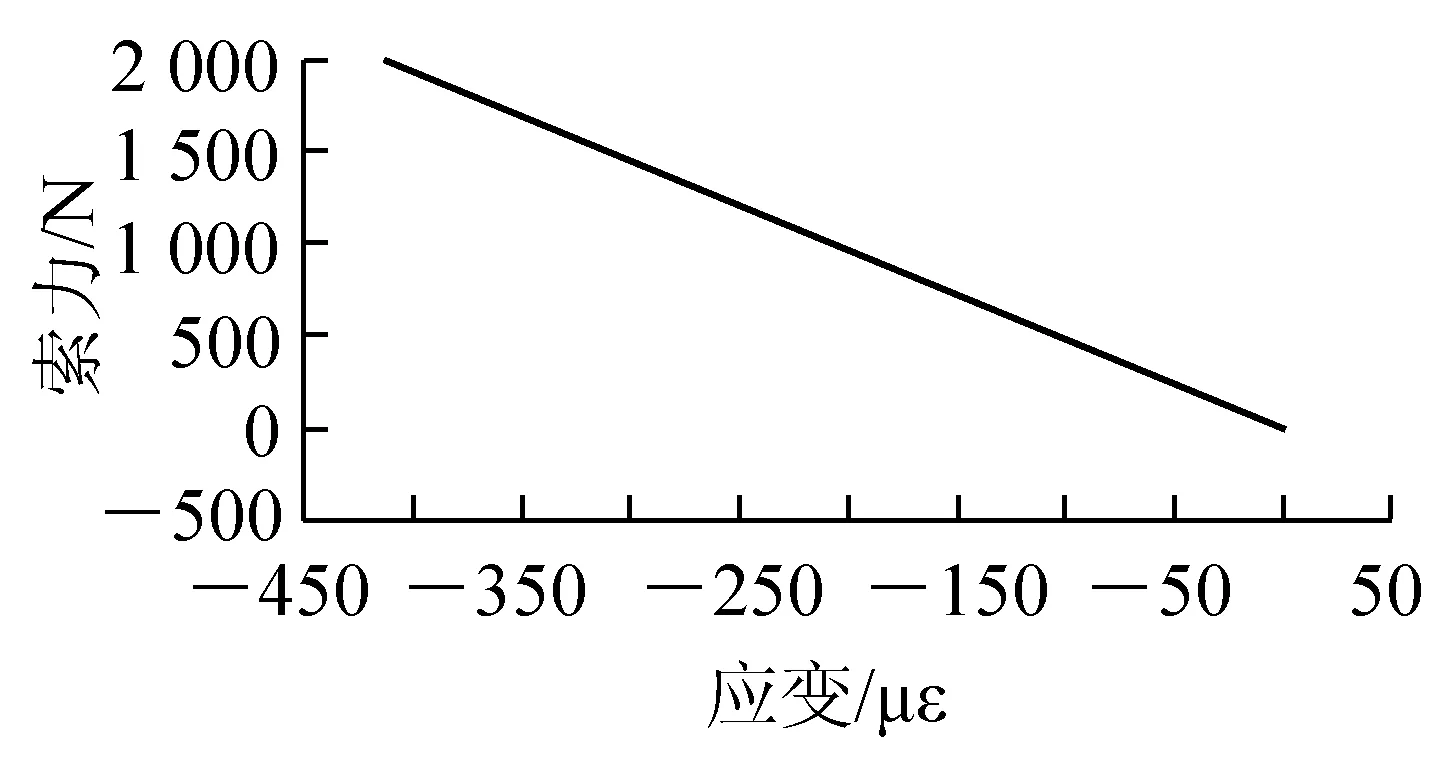
图4 索力与应变关系曲线

从表1、表2可以看出：传感器的倾角改变、斜拉索长度的改变均不影响传感器的应变值。从表3可以看出：斜拉索索力是影响压力环传感器应变的直接和主要因素，根据表中数值，做出斜拉索索力与压力环传感器应变之间的关系曲线如图4所示。

按照最小二乘方法，将曲线拟合成曲线，曲线方程为

F=-4.838 3ε+0.001 7

(1)

式中,ε为压力环传感器测试的微应变。

3 试验验证

为验证基于压力环传感器的索力测试系统的工作性能，采用测频法进行了对比试验。考虑到实验室场地条件的限制，斜拉索索长较短，且质量很小，为提高测频法的精度，选用了北京东方振动和噪声技术研究所研发的ICP加速度传感器，该传感器质量非常小，测试精度较高，其规格型号为INV9824，灵敏度为5 mV/g，频率范围为1～15 kHz，传感器自重为8 g，量程为1 000 g，谐振频率为40 kHz。加速度传感器测试数据的采集和分析系统选用了东方所开发的与之配套的DASP动态信号测试和分析系统。

在试验平台上，安装斜拉索，将压力环传感器索力测试系统调零，调节调索螺栓，使斜拉索张紧，记录静态应变仪测量的应变，根据式(1)式计算压力环传感器测试的斜拉索索力；然后采用敲击的方式对斜拉索进行激振，用加速度传感器进行测量，并用信号分析处理系统计算斜拉索索力，将两者测量结果进行对比。限于篇幅，给出了第9组斜拉索加速度传感器测试索力的频谱曲线如图5所示。从图5可知，该组斜拉索的基频为13 Hz，该组斜拉索索长2.745 m，单位索重为0.22 kg/m，由此由DASP动态信号分析系统可求出该索的索力为1 120.6 N。其余拉索的分析过程从略，仅给出最终索力分析值与压力环传感器的测量结果汇总于表4中。

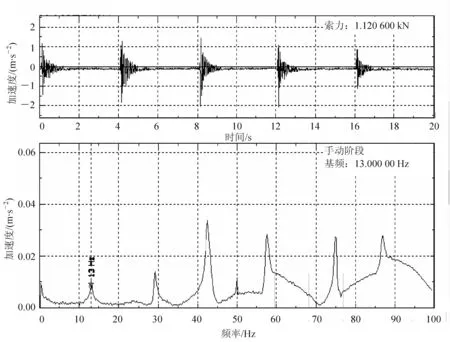
图5 9#拉索加速度传感器索力测试频谱分析

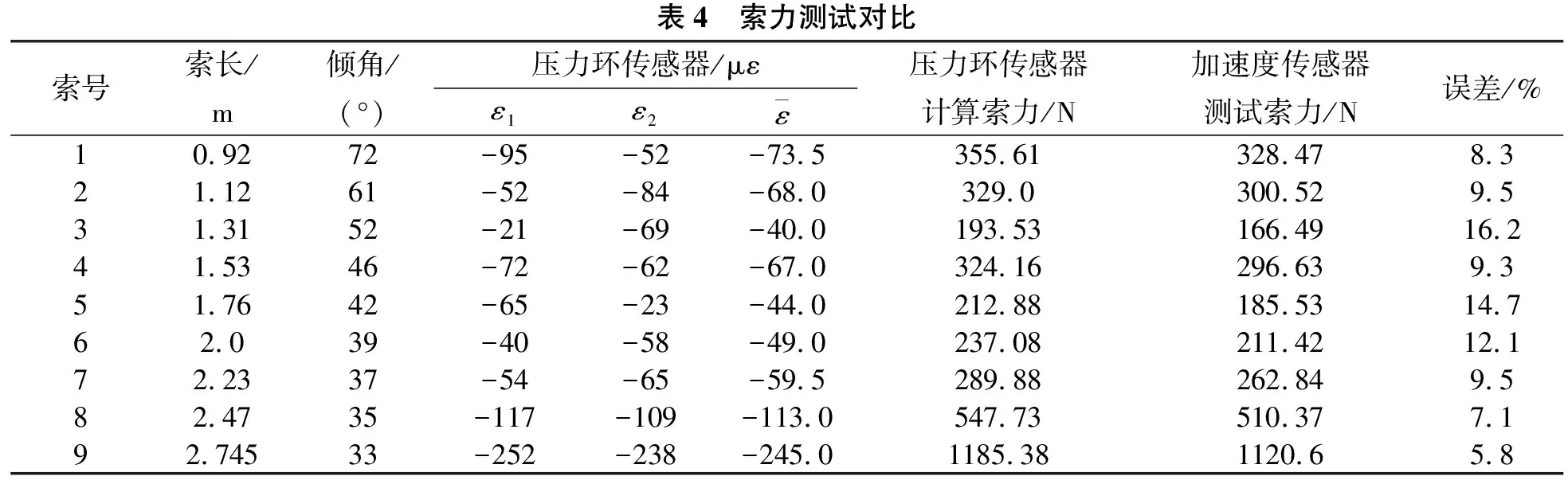
表4 索力测试对比索号索长/m倾角/(°)压力环传感器/μεε1ε2 ε压力环传感器计算索力/N加速度传感器测试索力/N误差/%10.9272-95-52-73.5355.61328.478.321.1261-52-84-68.0329.0300.529.531.3152-21-69-40.0193.53166.4916.241.5346-72-62-67.0324.16296.639.351.7642-65-23-44.0212.88185.5314.762.039-40-58-49.0237.08211.4212.172.2337-54-65-59.5289.88262.849.582.4735-117-109-113.0547.73510.377.192.74533-252-238-245.01185.381120.65.8

从表4可以看出：采用本文自制的压力环传感器测试斜拉索的索力与采用加速度传感器测试的索力吻合情况良好，随着索力的增加，两者之间的误差也越来越小。这表明本文提出的压力环传感器测试索力的方法是可靠的，压力环传感器性能稳定，测试结果准确。同时从表4中可以看出：压力环传感器的测试结果较加速度传感器的测试结果大。由于受到实验室条件的限制，本文的斜拉索索长均较短，根据现有文献可认为加速度传感器的测试结果误差较大，这也在一定程度上反映了压力环传感器测试结果的精度较高。

4 结论

斜拉索的索力测试一直是工程界关注的重点问题。本文为解决斜拉桥模型试验中索力测试的难题，研发了一种基于压力环传感器的索力测试系统。结合Ansys分析软件，对该系统按照接触问题进行了仿真分析，得到了索力与测试应变的函数关系式。同时在实验室将该系统的测试结果与传统的测频法的测试结果进行了对比验证，结果表明：本章研发的索力测试系统性能可靠，操作方便，测试结果精度较高，当选择合适的传感元件时，该系统可应用于斜拉索索力的长期、实时监测。

参 考 文 献

[1]李佳升,颜东煌,田仲初.三塔斜拉桥整体模型试验的实施[J].长沙交通学院学报,1999,15(3):34-37.

[2]李亚非,颜东煌,田仲初.大型三塔斜拉桥铝合金试验模型的研制[J].长沙交通学院学报,2000,16(3):37-41.

[3]安群慧,刘自明.荆州长江公路桥整体模型试验研究[J].桥梁建设,2002(2):15-18.

[4]余毅,余天乐,乐韩燕.吉林兰旗松花江特大桥施工阶段及成桥静力模型制作[J].世界桥梁,2008(1):73-75.

[5]刘兆丰,戴显荣,赵人达,等. 双塔联体分幅斜拉桥塔结构模型试验索力测试结果分析[J].实验力学,2009,24(6):573-578.

[6]葛继平,李胡生. 基于柔度变化率的独塔斜拉桥模型损伤识别试验研究[J]. 上海应用技术学院学报:自然科学版,2010,10(1):38-43.

[7]李延强,杜彦良.面向损伤识别的独塔斜拉桥模型的设计与分析[J].石家庄铁道大学学报:自然科学版,2012,35(3):6-9