预应力薄壁箱梁受弯剪力滞效应分析

, ,

(同济大学 桥梁工程系，上海 200092)

1 剪力滞效应原理

在传统意义上，在箱型梁中，产生弯曲的剪力流通过肋板传递给翼板，剪力在翼缘板上分布是不均匀的，从而引起弯曲时远离肋板的翼缘纵向位移滞后于近肋板的翼缘纵向位移，或者反之，这就导致其弯曲正应力的横向分布呈曲线形，这种由于翼缘的剪切变形所造成的弯曲正应力沿桥宽方向不均匀的现象称为“剪力滞效应”。通常用剪力滞系数来度量剪力滞效应的变化规律[1-2]，即

对于受弯箱梁，上下翼缘板的纵向位移函数可表示为只含一个量测剪滞效应尺寸的腹板最大纵向位移差函数U(x)和竖向位移函数w(x)的泛函，然而，若箱梁再受到轴心或偏心压力时，除上述者外，尚需增设另一个量测剪滞效应尺度的腹板最大纵向位移差函数ξ1(x)和轴向位移函数D(x)[3]。此时这种受力状态产生的箱梁正应力分布不均匀现象已经脱离了传统意义上的箱梁剪力滞的范畴，因为腹板内的平面假定已不再适用。当箱梁受到偏心预应力作用时，箱梁截面产生的正应力分布不均匀现象已经不符合传统意义上的箱梁剪力滞概念，有可能是由于薄壁箱梁的空间几何特性，使得其在不同的荷载形式下，正应力在传递的过程中出现分布不均匀现象，也就是通常所说的“圣维南原理”，也有可能仍然是由于翼缘板上分布不均匀的剪力流引起，本文所涉及到的几种荷载条件有单纯预应力作用，预应力与自重、活载(等效车轮荷载)共同作用，自重与活载对箱梁产生的翼缘板正应力不均匀分布是典型的剪力滞现象，为了统一，本文暂且先把预应力作用下箱梁翼缘板的正应力分布不均匀系数也称为“剪力滞现象”，正应力不均匀系数统称为剪力滞系数，是不是真的由翼缘板上不均匀分布的剪力流引起的，还需要进一步讨论研究才能得出结论。

本文将采用文献[2]中介绍的有机玻璃简支梁模型作为计算模型，利用实体单元建立对应的有限元模型，在有限元分析软件ANSYS中进行分析求解，将数值计算结果与文献中的计算值及试验数值进行比较，对计算单元的选择与数值计算方法的正确性进行验证。对于进入塑性阶段的箱梁截面的剪力滞效应，与弹性阶段的区别也需要进一步计算才能得出相应的结论。

2 预应力薄壁直线箱梁的剪力滞效应分析

2.1 有限元模型的建立

利用文献[2]中所使用的简支直线有机玻璃薄壁试验箱梁模型，跨径L为80 cm，材料的弹性模量为E=3 000 MPa，泊松比μ=0.385，横截面尺寸如图1。

用ANSYS建立的SOLID95模型，总共有87 024个节点，15 682个单元，如图2所示。

图1 箱梁横断面及测点位置(单位：cm) 图2 有限元模型

2.2 计算结果的准确性分析

文献[2]中的数值计算结果是利用ANSYS的板单元SHELL63建模得到的，加载条件一样，即忽略自重，在简支直线箱梁跨中正对腹板的上翼缘板处作用对称集中荷载，总量为P=0.272 2 kN，为了验证本模型的正确性，对比二者结果如表1。

表1 简支直线箱梁跨中截面正应力计算结果MPa位置测点编号本研究计算值文献计算值变分法计算值试验数据悬1-0.202 74-0.225 83-0.242 45-0.212 24臂2-0.238 09-0.244 41-0.257 28-0.248 50板3-0.289 18-0.284 82-0.361 03-0.329 004-0.402 98-0.387 61-0.407 40—上5-0.404 14-0.387 61-0.407 40—顶6-0.303 31-0.312 56-0.361 03-0.320 04板7-0.267 84-0.283 15-0.257 28-0.260 408-0.258 16-0.274 62-0.242 45-0.245 00下110.742 660.639 670.669 29—顶120.465 660.482 560.593 130.573 76板130.411 030.436 790.442 670.398 40140.396 470.423 510.398 320.388 80

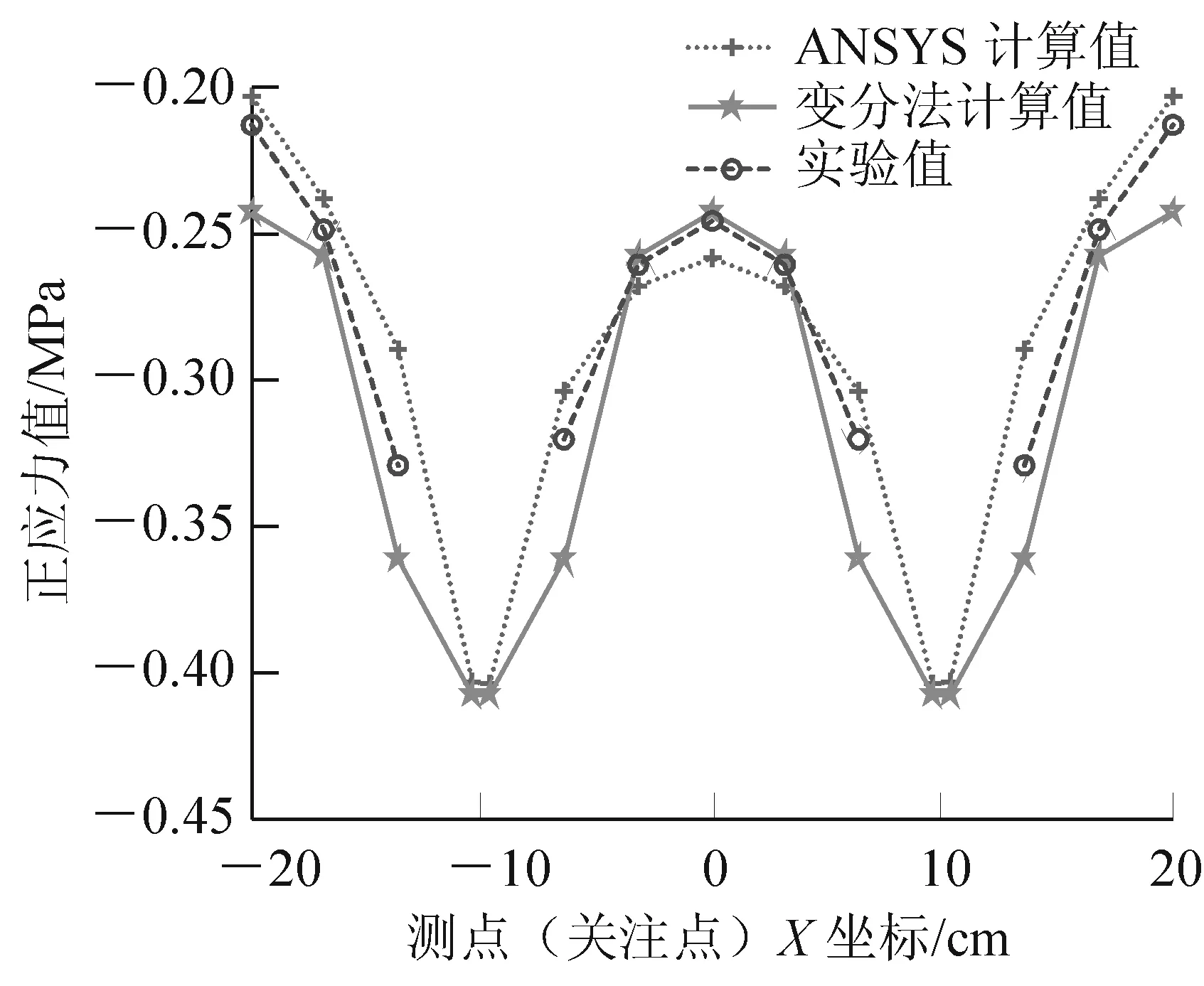
图3 直线箱梁跨中截面顶板轴向正应力分布图

从表1中可以看到，利用ANSYS有限元分析软件建立的SOLID95模型得到的数值解与文献[2]用板单元SHELL63建立的模型计算结果基本相吻合，某些点的应力甚至比文献[2]的应力更加接近实验值。其中，数值计算解与变分法理论计算值误差在16.4%以内，与试验数据的误差只有两个点超过6%，其余点均在6%以内。以跨中截面上顶板正应力为例，如图3所示，表示的是本研究用ANSYS模型计算的跨中上顶板正应力与用变分法理论计算结果和该有机玻璃模型梁试验结果的对比图。

由图3可见，由ANSYS求解出来的计算结果精度较高，能够真实反映横断面上应力的分布情况，为后面深入研究打下基础。

2.3 预应力受弯箱梁剪力滞效应

为了得到箱梁翼缘板的准确正应力，将预应力加在两腹板上的点10位置处，如图1所示，两根钢束的预应力合力大小均为300 N。在ANSYS中利用LINK8单元模拟预应力作用，通过赋予初始应变得到所需预应力。研究初期，也曾用等效荷载加在同一位置处，提取的结果和用LINK8单元算出来的结果进行对比分析，最后发现误差较小，说明用LINK8单元模拟纵向预应力筋是准确的。跨中施加的集中荷载P亦可模拟车轮荷载作用下在跨中的等效集中力。

2.3.1 仅轴力、纯弯荷载作用下的箱梁剪力滞纵向效应分析

当在腹板上质心位置上下距离1.1 cm处对称作用方向相反的两排共四根均为300 N预应力时，由于轴力相互平衡，在截面只产生纯弯荷载，而当预应力加在质心位置时，仅产生轴力。有必要研究在这两种情况下剪力滞系数沿跨径方向(纵向)的分布。取跨径L=2 m，分别画出两种荷载下的剪力滞系数纵向分布图，如图4所示，横坐标表示的是跨径长度范围，纵坐标表示剪力滞系数λ。

由图4知，仅轴力作用和纯弯作用下的剪力滞系数沿纵向分布的趋势基本相同，仅轴力作用下和纯弯荷载作用下，根据圣维南原理，在靠近支座的一段长度范围内应力是不符合平面均匀受压状态的。纯弯状态下或者仅轴力作用下离作用点越远即越靠近跨中位置就越符合平面变形状态，这些区段剪力滞现象是不存在的。如图5所示，在过渡段仍分布有剪应力，说明梁端附近的过渡段是存在剪力滞效应的。这部分剪力滞现象是由于预应力锚固端及梁端板壁纵向自由变形时产生的。

图4 两种荷载下 纵向分布对比 图5 两种荷载下剪应力纵向分布对比

不仅如此，通过大量有限元分析结果表明，当荷载形式不变，仅改变荷载大小时，仅轴力作用和纯弯矩作用下，存在剪力滞的过渡段长度大致相同，均为距支点约两倍腹板净距。

可见在偏心的预应力作用下，剪应力分布图更接近于仅轴力作用时的分布图。由文献[4]关于剪力滞系数分析可知，箱梁截面总的剪力滞系数λ取决于截面轴力的偏心距，轴力与弯矩在截面内力贡献比较分析中，偏心距越小，箱梁截面总的剪力滞产生的剪力滞效应越接近于仅受到轴力作用的状态。本文在测点10处施加预应力时，截面的弯矩与轴力之比约为0.05，所以截面剪力滞系数更接近于仅受轴向荷载作用下的情况，偏心预应力作用下的剪力滞效应也可以理解为轴力和弯矩产生的剪力流在横断面联合作用的结果，剪力滞系数靠近支点附近的最大值没有仅轴力和纯弯作用下大，主要是因为在靠近支点附近处轴压力和弯矩在翼缘板产生的剪力流方向相反，抵消了一部分轴压力作用下剪力滞效应。

2.3.2 预应力箱梁“剪力滞”纵向效应分析

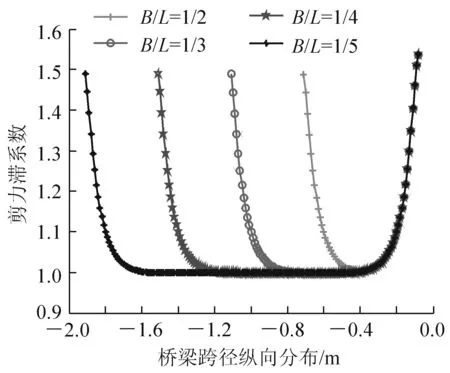
图6 不同宽跨比的 纵向分布图

为了研究箱梁剪力滞系数沿纵向的分布，选取横断面的最大剪力滞系数也就是正对腹板的上翼缘板中心处作为控制点，绘出剪力滞系数沿纵向的变化趋势，如图6所示。先对宽跨比这个影响因素进行分析，其中横断面的几何参数不变，取跨径L分别为0.8 m，1.2 m，1.6 m，2.0 m。以下如未作特别说明，横坐标表示的是跨径长度范围，纵坐标表示剪力滞系数λ。

由图6知，在相同的预应力作用下，只改变跨径，该简支箱梁在不同的宽跨比下剪力滞系数沿纵向变化趋势一致。从梁端到跨中的过渡段存在剪力滞效应，而跨中几乎不受剪力滞的影响。

文献[3]中提到的，当模型桥仅受轴向荷载时，翼板与腹板交界处剪力滞系数沿着跨径变化曲线，影响区域大致在距离梁端部两倍的腹板之间净距的长度范围内。本文加预应力后属于偏心受压，说明在压弯荷载作用下，宽跨比不会影响存在剪力滞系数的过渡段长度。为了验证过渡段正应力分布不均匀效应仍然和翼缘板上不均匀分布的剪应力有关，取出当跨径为2 m时从支点Z=-2 m到Z=-1.8 m区域内间距为0.1 m的三个横断面剪应力，如图7所示。

由图7可知，越靠近跨中横断面剪应力的分布越均匀，在Z=-1.8 m到Z=-2 m区域内，剪力沿着横断面的整体变化幅度为先增大后减小，Z=-1.8 m到Z=-1.9 m处在过渡段，横断面的剪应力在逐渐增加。

由文献[4]关于剪力滞系数分析可知，箱梁截面总的剪力滞系数λ取决于偏心距，偏心距越小，箱梁截面总的剪力滞产生的剪力滞效应越接近于仅受到轴力作用的状态。本文仅施加预应力时，偏心距较小，所以截面剪力滞系数更接近于仅受轴向荷载作用下的弯矩。与文献[3]中所得出的跨中剪力滞系数相近，箱梁顶板的剪力滞系数峰值(正对腹板的上翼缘板处)均为1左右，进一步说明了本文的数值解是符合解析解的。

跨径取为0.8 m，改变腹板厚度时，在翼缘板同一位置得到剪力滞系数沿跨径的分布如图8所示。

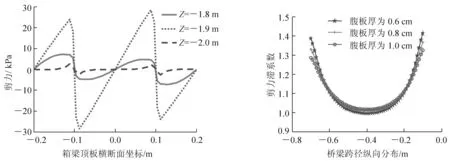
图7 各横断面剪应力分布图 图8 腹板厚度变化的 纵向分布对比

当腹板越来越厚时，靠近支座的剪力滞系数和剪力滞系数峰值有所减小，其他位置的剪力滞系数差别不是很大。腹板越厚，剪力滞系数的纵向分布趋势将越均匀。

综上所述，对于轴向力产生的压弯荷载，宽跨比对剪力滞系数沿着跨径的纵向分布没有影响，腹板厚度越小，在支点附近产生的剪力滞极值越大。

2.3.3 预应力度对于预应力简支箱梁剪力滞纵向分布的影响分析

恒载、活载对于大部分公路简支箱梁桥来说是需要主要考虑的荷载，研究预应力简支箱梁在这两种荷载下的剪力滞效应是相当有必要的。本文将箱梁的自重和等效的车轮集中力加上，得到不同的预应力度下的剪力滞系数沿跨径的纵向分布。本小节所有横向坐标表示的都是桥梁纵向位置坐标，分别取预应力度为1(跨中截面底板无拉应力)和0.5(部分预应力结构)，得到如图9所示。

图9 考虑自重的四种情况下顶板 纵向分布图

分析图9变化规律得到，在自重(均布荷载)作用下，箱梁顶板的剪力滞系数沿纵向分布均为正剪力滞，同时，越靠近支点处的剪力滞系数越大，和解析解得出的规律相同。预应力度越大时，箱梁顶板的压应力会变小，同时剪力滞系数也变小，说明对于这种宽大薄壁箱梁截面，加预应力可以在减小其受压区压应力的同时减小其受压区混凝土的剪力滞系数。

除了恒载的作用，还有活载对预应力箱梁的影响也是需要注意的。假设前述的P等效为车轮荷载作用。

暂不考虑总重，为了平衡跨中的活载，同前，当预应力度分别取为1和0.5时得到的剪力滞系数沿着跨径方向的变化曲线如图10所示。

在跨中集中力作用下，顶板剪力滞系数出现峰值，大约为1.4，之后远离集中力逐渐减小，但是靠近支座附近又呈现逐渐增大的趋势，而加预应力后，跨中剪力滞系数峰值约为1.3，说明预应力对跨中剪力滞系数和靠近支座附近的剪力滞系数都有“削峰”的作用。

当降低预应力度降低为0.5时，跨中截面的剪力滞系数的峰值变大，对于结构来说是不利的。这也说明了，全预应力混凝土箱梁的剪力滞系数要小于部分预应力混凝土箱梁，可以降低剪力滞对于截面受力的影响。

考虑自重、跨中车轮荷载、预应力三者共同作用时的剪力滞系数沿跨径分布如图11所示，仍取预应力度为1时，也就是预应力恰好平衡掉由活载和自重产生的跨中截面底板的拉应力，此时，剪力滞系数沿纵向分布又发生了变化，变得较为均匀，且跨中截面的最大剪力滞系数变为1.2左右。对于跨径较大的箱梁桥时，总重所占的比重更大，采用全预应力减小剪力滞系数的效果更好，相对于短跨径而言，效益更好。

图10 考虑活载的四种情况下顶板 纵向分布图 图11 自重、活载均考虑时顶板 纵向分布对比图

3 塑性阶段箱梁剪力滞效应

进入塑性阶段箱梁的剪力滞效应研究尚少，本文在ANSYS中用solid65单元建立了一个简单的悬臂钢箱梁模型，横断面如图12所示。

由于在ANSYS中计算材料非线性问题时，用混凝土材料较难收敛，所以本例中采用了悬臂钢箱梁模型，本小节分析的均为固端截面，由解析解知该截面存在的是正剪力滞，主要比较受压区钢材屈服时的剪力滞系数与弹性阶段的变化。钢材的弹塑性曲线的屈服应力为235 MPa，切线模量为790 MPa。采用双线性随动强化模型BKIN。荷载形式为加在翼缘板上的面均布荷载。由于截面几何特性，得到中性轴距离翼缘板更近，因而底板比翼缘板先达到屈服压应力。

当底板最外缘拉应力达到235 MPa时底板的剪力滞系数分布图如图13所示。此时，塑性阶段的剪力滞系数是通过数值计算的结果除以屈服应力235 MPa得到。从ANSYS中提取固端正应力结果后，此时底板最外侧几个点的正应力已经超过屈服应力235 MPa，其他大部分点均未达到屈服应力，说明在这种均布荷载作用下各点的剪力滞系数与弹性阶段剪力滞系数分布都差不多，同时截面的应力分布还处于弹性阶段的状态，模型的塑性变形不明显，主要是弹性阶段的变形。

当在模型上加了对应于1.5倍屈服弯矩的均布荷载后，截面底板受压区的压应力分布较均匀，正剪力滞效应较大，同时，正应力分布规律体现出受压区基本进入塑性状态，如图13所示。

图12 钢箱梁横断面(单位：cm) 图13 箱梁底板正应力分布(单位：m)

图14 箱梁竖向正应力分布图

当箱梁的固端最大弯矩为1.5倍屈服弯矩时，其截面从底板到受压区腹板的正应力分布较恰好达到屈服弯矩时均匀，如图14所示，同时，受压区腹板的压应力也很大，接近屈服应力，而顶板的拉应力增幅较大并接近屈服。此时整个模型的塑性变形比弹性变形要大很多。综上所述，在1.5倍的屈服弯矩加上去之后，箱梁截面底板正应力的变化和箱梁竖向正应力的变化均较大，底板正应力趋向于平均，剪力滞效应影响减弱，而竖向正应力也趋向于平均，伴随较大塑性变形进入塑性状态。

如图15所示，随着翼缘板上均布荷载的增加，悬臂箱梁的悬臂端最大竖向位移值呈现出从弹性到塑性阶段应有的特性，即先线形增加后进入平缓段。拐点位置处所施加的均布荷载大约为440 kN/m，比理论值计算出来的使得底板最外边缘恰好达到屈服应力的356 kN/m大。

底板剪应力分析结果见图16，由于剪力滞效应的存在使得截面进入塑性阶段的过程较为缓慢，同时，底板在未进入塑性阶段之前的剪力相差较小，进入塑性状态后，截面剪力的绝对值增量幅度明显增大。

图15 均布荷载与最大竖向位移关系图 图16 箱梁底板剪应力分布图

4 结论

通过ANSYS数值计算与分析，可以得到以下结论：

(1)仅在预应力作用下，箱梁翼缘板上产生的正应力不均匀分布现象，仍然符合传统意义上关于剪力滞的定义，即由于翼缘板不均匀剪力流引起的，所以引用剪力滞概念来描述这种正应力不均匀分布现象是有理论依据的。由本研究得出来的结论如下：宽跨比对于箱梁剪力滞系数沿着纵向分布没有影响；腹板越来越厚时，靠近支座的剪力滞系数和剪力滞系数峰值有所减小，其他位置的剪力滞系数差别不是很大。

(3)仅轴力作用和纯弯矩作用下，存在剪力滞的过渡段长度大致相同，均为距支点约两倍腹板净距，同时剪力沿跨径在剪力滞影响区域的纵向变化趋势两者刚好相反。

(3)分别考虑自重，等效车轮荷载，及其共同作用时剪力滞系数的纵向分布得到的结论是：全预应力结构使得剪力滞系数纵向分布较为均衡，且就有较好的“削峰”效果。

(4)由于箱梁剪力滞效应的存在，箱梁进入塑性阶段过程较缓慢，同时，进入塑性变形之后的截面剪力较弹性变形阶段的增幅会突然变大，剪力滞效应更加明显。

参 考 文 献

[1]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001:315.

[2]徐飞鸿，蔡汶珊.薄壁箱梁剪力滞效应数值计算[J].长沙理工大学学报:自然科学版,2009(4):16-20.

[3]罗旗帜.箱梁在压弯荷载共同作用下的剪力滞[J].土木工程学报,1991,24(1):52-64.

[4]贾涛.马新大桥斜独塔单索面斜拉桥箱形主梁剪力滞效应及计算方法研究[D].兰州:兰州交通大学土木工程学院,2009.