基于共振解调的铁路货车轴承故障诊断

, ， ，

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

0 引言

轮对滚动轴承是机车的重要部件，其工作状态是否完好直接影响机车能否安全运行。不同的故障形式和位置具有不同的故障特征频率，因此可以通过分析滚动轴承运行时的振动信号推断可能存在的故障类型。铁路货车轴承为双列圆锥滚子轴承，由于双列圆锥滚子轴承结构复杂、故障特征频率难以精确计算，而早期微弱故障往往又淹没于系统噪声而难于提取，因此采用传统方法进行故障精密诊断十分困难。目前常用的故障诊断方法有小波变换[1]、盲信号分离技术[2-3]和Hilbert-Huang变换[4-5]等，但是这些方法都存在一定的缺陷，如盲信号分离技术需要预知原信号的数量并且对于卷积混合、非线性混合等问题处理难度较大，Hilbert-Huang变换中边界效应问题不能彻底解决[6]。由于共振解调技术具有选择性、放大性、比例性、展宽性、低频性和多阶性[7-8]等优点被广泛应用于轴承的故障诊断中。本文将共振解调技术应用于铁路货车轴承的早期故障诊断中，得到了很好的结果。

1 滚动轴承诊断机理

机车滚动轴承有多种故障形式，常见的有压痕、剥离、电蚀、断裂等，发生部位分别为外圈、内圈、滚子和保持架。当上述任一部位发生故障时都会产生一定的均匀间隔的冲击脉冲力从而产生振动冲击信号，进而出现轴承的故障特征频率[9]。文献[10]给出了滚动轴承不同故障特征频率的计算方法。

外圈故障特征频率为

(1)

内圈故障特征频率为

(2)

滚子故障特征频率为

(3)

保持架故障特征频率为

(4)

式中，轴承内圈转动频率fr=N/60，N为内圈转速;D为轴承节径;d为滚子直径;∂为接触角;z为滚子个数。

2 共振解调原理

共振解调技术是从振动检测技术中发展起来的一种故障特征提取方法，又称包络解调法。其原理简述如下[11]：当轴承某一元件表面产生局部损伤时，在运行过程中要撞击与之相互作用的其它元件表面，除了产生含有故障特征频率的低频振动外，还会产生冲击脉冲力。由于脉冲力的频带很宽，必然包含轴承外圈、传感器甚至整个机械系统的固有频率而激起这个测振系统的高频固有振动。根据实际情况，可选择某一高频固有振动作为研究对象，通过带通滤波器把该振动分离出来。然后通过包络检波，去除高频衰减振动的频率成分，得到只包含故障特征信息的低频包络信号。最后对这一包络信号进行频谱分析从而诊断出轴承的故障。

共振解调技术具有以下特点[7]：①每一次冲击都对应激发一次共振解调波，不遗漏任何一次由故障引起的冲击，即一一对应性；②只有故障冲击才能激发共振解调波，正常振动不能激发共振解调波，即选择性；③微小的故障冲击就能激发很大的共振解调波，即放大性；④共振解调波的幅度与原始故障冲击幅度成正比例关系，即比例性；⑤原始故障冲击波经共振解调后被展宽，且展宽的程度与共振频率和冲击的频率无关，即展宽性；⑥共振解调将故障冲击的高频能量调理为低频信号的形式出现，即低频性；⑦共振解调波的频谱为等间距的梳状谱线，即多阶性。以上特点能够保证该方法有效地将故障特征频率从复杂的干扰信号中提取出来，准确的实现故障诊断。

由于铁路货车轴承为双列圆锥滚子轴承，而双列圆锥滚子轴承结构复杂、故障特征频率难以精确计算，且早期微弱故障往往又淹没于系统噪声而难于提取，加之各种频率成分交加使得频率成分更加复杂，因此采用传统方法进行故障精密诊断十分困难，直接对其进行频谱分析往往不能成功，所以可借助共振解调技术对采集的振动信号进行分析与处理。

通过软件实现共振解调的主要分以下4个步骤：①对时域信号进行谱分析，找到机械谐振的共振频率带，并对此共振频率带进行带通滤波；②对滤波后的信号进行希尔伯特变换；③构造希尔伯特变换后信号的包络线；④对包络后的信号进行低通滤波并作谱分析。可用图1表示。

图1 共振解调原理

其中采用希尔伯特变换对信号进行包络解调是该技术中的重要环节。希尔伯特变换可以看成是信号通过一个幅度为1的全通滤波器的输出，它常用于提取信号的瞬时相位，获取振荡信号的包络等。

设给定信号为x(t)，其希尔伯特变换定义为

(5)

令h(t)=1/πt，对其进行傅里叶变换可得

(6)

(7)

由此可得到信号的包络曲线方程为

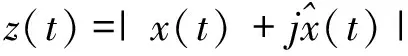
(8)

式(8)即为信号的包络信号，对其进行谱分析即可得到多阶解调谱的特征。

3 实验研究

为了验证该方法的有效性，将该方法应用于实测故障滚动轴承的信号中。实验在如图2所示的铁路货车轮对滚动轴承故障诊断实验台上完成。实验所用轴承是车辆厂提供的197726型故障轴承，其典型故障为外圈剥离和滚子剥离，同时选用与轮对匹配的正常轴承。实验所用的振动传感器为CA-YD-181-50型加速度传感器，分别安装在轮对滚动轴承右端轴承外圈和轴承座上，其中轴承座竖直方向(1通道)和水平方向(2通道)分别布置一个传感器，轴承外圈的水平方向(3通道)布置一个传感器，其传感器布置如图3所示。

三个通道的振动加速度信号通过信号调理器和INV36DF型信号采集处理仪采集得到，输入到电脑中由与之相配套的DASP软件纪录和存储。

图2 轮对滚动轴承故障诊断实验台 图3 传感器布置图

表1列出了滚动轴承实验的工况，所用的197726型轴承轴承节径D为178.8mm，滚子直径d为23.776 mm，滚子个数为20，接触角为10°，由公式(1)计算得出，外圈故障特征频率fo=67.4 Hz，滚子故障特征频率fb=28.3 Hz。

4 基于共振解调技术的滚动轴承故障特征提取

4.1 外圈故障分析

在实验台右侧换上外圈剥离故障的滚动轴承，轮对转速为465 r/min时轴承座竖直方向的传感器(即图3中1通道)所采集的振动加速度信号如图4所示，图5为其谱图，由于系统噪声干扰，两幅图都看不出故障所在，需要做进一步处理。

由图5知机械的共振频带在500 Hz以上，因此对其进行500～5 000 Hz的带通滤波得到如图6所示的频域波形，由于系统噪声淹没了故障频率，对滤波后的信号进行希尔伯特变换并取其包络得如图7所示波形，对其进行谱分析如图8，最后进行低通滤波并将得到的结果进行细化得到如图9所示结果。

由图9结果可以看出，频率在67.4、134.9、202.3处都出现了明显的峰值，且幅值随着频率的升高而递减，这些频率与理论计算得出的故障频率67.4 Hz及其2倍频134.8 Hz、3倍频 202.2 Hz都基本吻合；另外，在7.8 Hz以及15.6 Hz处也出现了峰值，初步分析该频率成分为轮对的转频及其二倍频。

4.2 滚子故障分析

在实验台右侧换上滚子剥离故障的滚动轴承，轮对转速为460 r/min时轴承座竖直方向的传感器(即图中1通道)所采集的振动加速度信号如图10所示，图11为其功率谱图，由于系统噪声干扰，两幅图同样看不出故障所在，需要做进一步处理。

图4 外圈剥离信号的时域波形 图5 外圈剥离信号的功率谱图

图6 外圈剥离信号带通滤波后的功率谱 图7 外圈剥离信号的包络波形

图8 外圈剥离包络信号的功率谱图 图9 外圈剥离信号共振解调的最终结果

图10 滚子剥离信号的时域波形 图11 滚子剥离信号的功率谱图

由图11知机械的共振频带在500 Hz以上，因此对其进行500～1 400 Hz的带通滤波并对滤波后的信号进行希尔伯特变换并取其包络得如图12所示波形，对其进行谱分析，最后进行相应的滤波并将得到的结果进行细化得到如图13所示结果。

图12 滚子剥离信号的包络波形 图13 滚子剥离信号共振解调的最终结果

由图13的结果可以看出，频率在27 Hz处出现了明显的峰值，与理论计算的滚子故障特征频率28.3 Hz非常接近，可以判定为滚动轴承的滚子发生了故障，但是结果不如外圈故障的明显，笔者分析原因如下：

当外圈发生故障时，损伤点的位置相对传感器不动，采集的信号比较简单；而当滚子出现故障时,损伤点的位置相对传感器随轴承的转动而周期性变化，此时传感器拾取的信号比较复杂，从而分析结果不如外圈故障那样明显。当滚子发生故障时通常会使振动受到滚动体公转频率的影响，图中的前几阶谱线即为滚动体的公转频率及其倍数，并且在67.4 Hz处也出现了峰值，初步分析该轴承的外圈也可能存在轻微的损伤。

5 结论

针对共振解调能够提取淹没在强噪声条件下故障轴承特征频率的特点，将其应用在铁路货车轮对双列圆锥滚子轴承的早期故障诊断中。通过实验证明共振解调可以有效的提取出故障特征频率，诊断出故障类型，是提取强背景噪声中微弱脉冲信号的有效方法。将共振解调技术应用于滚动轴承故障的自动诊断具有编程简单、可靠性高等优点，尤其当滚动轴承的多个元件同时存在随机故障时，应用一般的振动分析方法很难诊断，可以利用共振解调法对此类复杂故障作出精确诊断。

参 考 文 献

[1]Rubini R, Meneghetti U. Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearings[J]. Mechanical Systems and Signal Processing, 2001, 15 (2): 287-302.

[2]陈恩利，张玺，申永军，等.基于SVD降噪和盲信号分离的轴承故障诊断[J]. 振动与冲击，2012,31(23):185-190.

[3]Shen YJ, Yang SP. A New blind-source-separation method and its application to fault diagnosis of rolling bearing[J]. International Journal of Nonlinear Sciences and Numerical Simulation,2006,7(3):245-250.

[4]Yu Dejie, Cheng Junsheng, Yang Yu. Application of hilbert-huang transform method to gear fault diagnosis[J]. Editorial Office of Chinese Journal of Mechanical Engineering,2005,41(6):102-107.

[5]杨世锡, 胡劲松, 吴昭同, 等, 旋转机械振动信号基于 EMD 的希尔伯特变换和小波变换时频分析比较[J]. 中国电机工程学报，2003,23(6):102-107.

[6]申永军，张光明，祈玉玲,等.基于Gabor变换的自适应降噪方法[J]. 石家庄铁道大学学报:自然科学版，2010,23(2):69-73.

[7]唐德尧，王定晓，杨政明,等.共振解调技术与机车车辆传动装置故障诊断[J]. 电力机车技术，2002,25(5):1-5.

[8]Gao Lixin, Wang Dapeng, Liu Baohua ,et al. Study on application of resonance-demodulation technology in rolling bearing fault diagnosis[J]. Journal of Beijing University of Technology, 2007,33(1):1-5.

[9]王嘉乐，王灿，会强.基于虚拟仪器的机车滚动轴承故障诊断研究[J]. 石家庄铁道大学学报:自然科学版，2012,25(3)：87-91.

[10]虞和济． 振动诊断的工程应用[M]． 北京: 冶金工业出版社，1992．

[11] 李光，丛培田. 基于共振解调的滚动轴承故障诊断的研究与实现[J].机械工程师，2006，10：129-131.