微带线不连续性补偿方法仿真研究

陈 鹏，曹沐昀

(南京航空航天大学电子信息工程学院，江苏南京 210016)

在微波网络的众多传输方式中，以微带线为核心的微带电路，因其加工制造过程简单，且方便将有源和无源器件进行集成，在实际微波电路系统应用中得到了广泛的应用。但在微带元件和电路的设计中，将不可避免地涉及到弯曲、宽度变化、T形分支、截断或隙缝等不连续性。这些不连续性将对微带中的电磁场分布产生影响，从等效电路上看，不连续性相当于并联或串联一些电抗元件，使电路参量发生变化。例如一些微波元件在设计上必须要有折弯，如定向耦合器、滤波器和功率分配器等，就将引入微带线的直角拐弯这类不连续性［1］。

通常有两种方法可消除微带电路中不连续性所带来的效应。方法一:在原有微带电路的基础上，通过建立该不连续性的等效电路，将这些由不连续性所造成的参数一并考虑进电路的设计中，通过调节其他的电路参量来补偿。该方法对于设计者的自身能力要求较高，需要精通各种情况所对应的等效电路。方法二:采用对微带线进行削角或斜拼接的方式来补偿不连续性［2］。

在文献［1～2］中，虽有较为详细的微带线不连续性补偿方法介绍及分析，但对于不同方法对补偿效果的具体影响以及同一种方法不同尺寸对于补偿效果的影响未予以深究。文中在文献［1～2］的理论基础上，采用基于有限元的3D电磁仿真软件Ansoft HFSS软件［3］进行仿真。在HFSS中，通过一个线性变化的变量模拟出不同尺寸削角和扫掠的情况，进行优化仿真，定量地分析不同尺寸的削角和扫掠处理对于不连续性补偿的效果及优缺点。

1 削角补偿方式仿真设计原理和思路

微带线直角拐弯会产生寄生的不连续性电容，其是由拐弯处附近微带线面积的增大所引起的。通过削角，可有效地减小拐弯处微带线的面积，从而降低直角拐弯所带来的多余电容效应［4］。

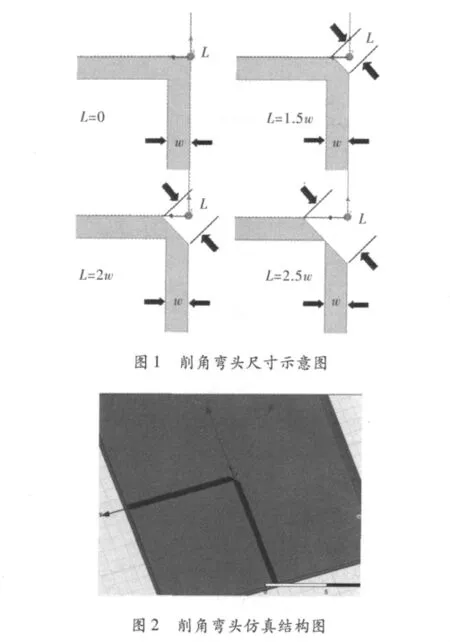
在仿真计算中，通过设置一个变量来实现，这一变量可直观地线性控制削角长度。且方便调节，并可对其进行优化仿真，如图1所示。图中W为微带线宽度，L即为削角尺寸长度。

在仿真中，通过设置一个中心原点，边长为2a的正方形作为切割体。该设置的优点为可通过改变a的值来改变正方形的边长。

再通过对这一正方形切割体，以z轴作为旋转轴，旋转90°达到切割的目的。这样切割线的长度就是文中设置的正方形边长。可以通过更改参数a的值来实现调节不同削角的长度，通过HFSS的优化仿真功能实现分析。从而精确地得到削角弯头补偿方式的最佳削角长度尺寸，具体仿真结构如图1和图2所示。

2 扫掠补偿方式仿真设计原理

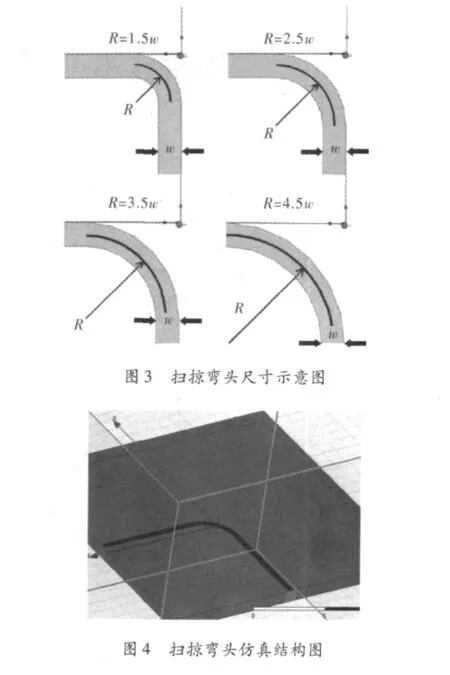
首先，通过一个半径为b+w/2，另一个半径为bw/2的两个半径相差w的圆相减得到一个宽度为w的圆环。随后通过削减整个圆环，得到1/4个圆环。最后，加上宽度为w的两个长方形得到最终R=b的微带线结构。由于b是一个线性可控制的变量，因此通过HFSS的优化仿真，能够精确得到扫掠弯头补偿方式的最佳尺寸R。具体仿真结构如图3和图4所示。

3 仿真结果

将HFSS的参数设置如下，材料是介电常数为3.5的Arlon AR 350，介质层高度0.88 mm，微带线宽度0.5 mm，outer边界为理想电边界，工作频段在1 GHz。

利用HFSS的优化仿真功能，利用范围0.325～0.575 mm，步距为0.05 mm的线性变量a，对削角弯头的削角尺寸L=2a进行控制，从而得到削角尺寸变化对于微带线不连续性的补偿效果进行了模拟仿真。根据第一次仿真结果，在削角尺寸2a=0.7 mm(1.4w)至1.0 mm(2w)时，增加敏感度，将步距改为0.001 mm。再次进行模拟仿真。仿真结果如图5和图6所示。

从图5和图6中可看出，当削角尺寸2a=0.796 mm即1.592w时，S12的值较大，为 －53.41 dB，而 S11的值较小，为－0.01 dB。该结论与工程上的要求基本相符。同时，在图中可发现，当2a=0.756 mm(削角尺寸为1.512w)时，S12的值最大为 －52.92 dB，而 S11的值较小，为－0.012 dB。另外，当2a=0.884～0.914 mm(削角尺寸为1.768～1.828w)时，S12的值较为稳定，为 －55.12 dB。在《Microwave Engineering》［2］一书中，提到的a=1.8w。也在文献［1～4］中提到最优参考值为a=1.6w。对比这些数据，说明了结果的正确性和可参考性。

利用了HFSS的优化仿真功能，利用范围从0.25～4.75 mm，步距为0.02 mm的线性变量b，对扫掠弯头的扫掠半径尺寸对于微带线不连续性的补偿效果进行了模拟仿真，仿真结果如图7和图8所示。

从图7和图8中可看出，当扫掠尺寸b=1.75 mm(扫掠尺寸=3w)时，S12的值较大为－54.90 dB，而S11的值较小为－0.010 dB。其对应的回波和插入损耗均较为理想，这与工程上要求的扫掠弯头尺寸通常＞3w基本相符。同时，从图中可以发现，当b=3.42 mm(扫掠尺寸为6.34w)时，S12的值最大为－50.99 dB，而S11的值较小为－0.013 dB。但在实际工程应用中，由于这种情况所占据的面积较大，因此使用较少。

4 结束语

实验结果表明，应用HFSS对微带线不连续性的不同补偿方式的效果进行仿真建模、优化以及测试，能够达到预期的效果。同时，对在工程上对于微带线的不连续性、不同补偿方式以及不同尺寸的补偿优劣给进行了比较，有一定参考价值。

［1］王文祥.微波工程技术［M］.北京:国防工业出版社，2009.

［2］DAVID M P.Microwave engineering［M］.3版，北京:电子工业出版社，2009.

［3］李明洋.HFSS应用详解［M］.北京:人民邮电出版社，2010.

［4］顾继慧.微波技术［M］.北京:科学出版社，2008.

［5］陈慰，赵娜，陶学敏.微带线不连续性补偿方法的HFSS仿真分析［J］.现代电子技术，2001，34(13):92－94.

［6］张栋.微带线直角拐角脉冲信号传输特性分析［J］.电子科技，2010，23(1):26 －28，40.