FMCW雷达发射泄漏信号数字对消技术研究

王 乐，习远望，刘 辉

(西安电子工程研究所人力资源部，陕西西安 710100)

由于受到体积、重量、成本等限制，多数导引头采用单天线技术［1－3］，导致收发隔离不足，使发射信号泄漏到接收机中，而信号泄漏可能导致连续波体制雷达接收机灵敏度下降，引起中放饱和、微波混频器或前置低噪声放大器饱和。

随着元器件的发展，毫米波前端器件的饱和功率，可达十几dBm以上，而在弹载环境中，连续波发射机功率一般在几百mW，因此，饱和不是主要问题，需重点解决泄漏导致接收机灵敏度下降问题。常用的射频对消技术虽然能有效地抑制发射泄漏信号，但在毫米波波段，没有矢量调制器可供使用，因此利用模拟的办法调整幅度和相位，难度较大。考虑到射频前端没有饱和，可以利用数字信号处理器数据处理能力强、准确灵活、通用能力强等优点，采用自适应数字对消技术使得由于收发隔离不足导致的发射泄漏信号得到最大限度的抑制。

1 自适应数字对消基本原理

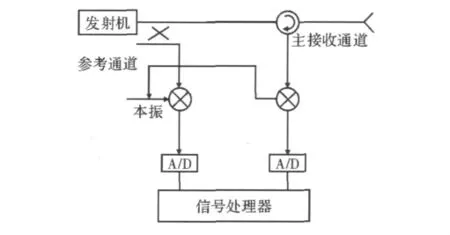
图1 自适应数字对消系统模型

波信号和参考信号分别送入中频自适应数字对消器，通过自适应调整参考信号的幅度和相位，使其与主路信号中发射泄漏信号幅度一致、相位相反，从而获得良好的对消效果。

自适应滤波器与普通滤波器不同，它的冲激响应或滤波参数随外部环境的变化而变化的，经过一段自动调节的收敛时间达到最佳滤波的要求。对消原理框图如图 2 所示［1－3］。

自适应数字对消系统模型如图1所示。

在该模型中，接收机有两个独立通道:参考接收通道和主接收通道。参考通道对发射信号进行采样，主接收通道包含发射泄漏信号和目标回波信号。将主回

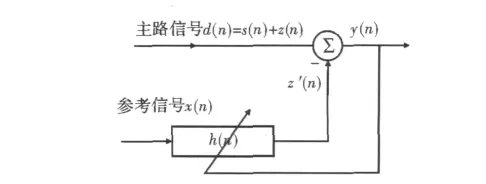
图2 对消原理框图

设主回波信号d(n)为目标回波信号s(n)与发射泄漏信号z(n)之和，x(n)为参考信号，x(n)与目标回波信号不相关，但与z(n)具有某种未知的相关性，x(n)经滤波后产生和z(n)极为相似的信号z'(n)，最终得到系统的输出y(n)=s(n)+z(n)－z'(n)。

假设z(n)、x(n)及s(n)是零均值的平稳随机过程。s(n)与z(n)不相关。而

对式(1)两边取数学期望，由于 s(n)与 z(n)、x(n)不相关，s(n)与z'(n)也不相关，故

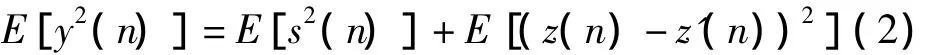
信号功率E［s2(n)］与自适应滤波器的调节无关，因此，自适应滤波器调节使 E［y2(n)］最小，就是E［(z(n)－z'(n))2］最小。又因为 z(n)－z'(n)=y(n)－s(n)，所以当 E［(z(n)－z'(n))2］最小时，自适应泄漏信号抵消系统的输出信号y(n)与有用信号s(n)的均方差E［y(n)－s(n))2］也最小，在理想情况下，z(n)=z'(n)，则 y(n)=s(n)。

自适应滤波器最重要的部分是自适应算法，算法可以根据输入、输出及原参量值，按照一定准则修改滤波参量，使自适应滤波器能有效地跟踪外部环境的变化。

目前，自适应滤波算法主要有以下3种［4－6］:

(1)基于维纳滤波器理论的最小均方误差LMS算法。该算法简单，运算量小，无需计算相关函数和矩阵求逆运算、易实现，在正确条件下可获得满意的性能。缺点是收敛速率较缓慢，对抽头输入相关矩阵的最大特征值与最小特征值之比变化敏感。即使这样，LMS算法仍然应用广泛。

(2)基于最小二乘法的递推最小二乘法RLS算法。该算法优点是收敛速度快，跟踪能力强，但由于需要进行矩阵求逆，计算量比LMS算法大，使其应用受到限制。

(3)基于卡尔曼滤波理论的卡尔曼算法。其收敛性能好、跟踪能力强、收敛速率具有鲁棒性(Robust)。对输入相关短阵特征值不敏感;并且，该算法适用于平稳随机过程和非平稳随机过程。缺点是该算法直接使用卡尔曼滤波公式中的矩阵表示式，算法复杂、运算量大、数值稳定性差。

文中选择LMS算法完成自适应数字对消。

2 理论数据仿真分析

设发射泄漏信号与参考信号均为20 MHz的正弦波，目标回波信号为21 MHz的正弦波，数据采样率为200 MHz。仿真结果如图3和图4所示［7］。

图3中，第一行窗口为对消前包含发射泄漏信号与参考信号的主回波信号d(n)，第二行窗口表示目标回波信号s(n)，第三行窗口表示对消后输出信号，可以看出，经过自适应调整，对消后的输出信号已看不到发射泄漏信号，由此可见，该系统对发射泄漏信号有较好的对消效果，波形失真小。

图4是信号响应的频域波形，第一行窗口对应主回波信号d(n)的频域图形，第二行窗口对应对消后输出信号的频域图形，根据仿真结果，泄漏信号约减小了39.46 dB。

3 实采数据实验验证

利用双音信号实采数据对以上仿真结果进行实验验证，实验系统框图如图5所示。

信号源1代表目标回波信号，信号源2代表发射泄漏信号，信号源1与信号源2的和信号通过功分器进入主接收通道，信号源2耦合出部分信号进入参考通道，两通道信号分别进行A/D转换后进入信号处理器完成泄漏对消。

图5 实验系统框图

实验时，发射泄漏信号与参考信号均为20 MHz的正弦波，目标回波信号为21 MHz的正弦波，数据采样率为200 MHz。信号响应时域波形如图6所示。

图6 信号响应时域波形

图6中，第一行窗口表示主回波信号d(n)，第二行窗口表示对消后输出信号，可以看出，对消后的输出基本上可以还原目标回波信号，波形失真小。

图7为图6所示信号对应的频域图形，为便于分析，将对消后信号频域图进行放大，如图8所示，经对比可知，泄漏信号约减小了32.23 dB。

图7 信号响应频域波形

图8 对消后信号频谱局部放大图

实采数据实验结果相对于理论仿真结果，泄漏信号抑制能力减小7 dB，主要是由于实采数据比理论仿真数据复杂得多，并且考虑到工程应用对时效性的要求，系统滤波参数的调整达不到仿真时的理想精度，因此导致抑制能力减弱。

4 结束语

文中通过理论分析和实验验证证实，针对调频连续波雷达发射信号泄漏问题，通过自适应数字对消技术，可以有效地减小发射泄漏信号，降低泄漏信号对接收机灵敏度的影响。理论仿真与实验测试结果证明该方法有效可行。

［1］张强.强噪声背景下噪声对消技术的研究［D］.大连:大连海事大学，2010.

［2］吕波，郑秋容，袁乃昌.一种改善雷达收发隔离的新方法［J］. 系统工程与电子技术，2008，30(8):1595 －1597.

［3］耿道田，刘峥.连续波体制雷达直波泄漏抑制方法与系统设计［J］.空军工程大学学报，2007(6):37－39.

［4］蒋云昊.辐射干扰对消系统自适应控制方法研究［D］.武汉:华中科技大学，2010.

［5］饶瑞楠.自适应对消的收发隔离技术［D］.西安:西安电子科技大学，2006.

［6］曹斌芳.自适应噪声抵消技术的研究［D］.长沙:湖南大学，2007.

［7］BASSEM R M，ATEF Z E.雷达系统设计Matlab仿真［M］.朱国富，译.北京:电子工业出版社，2009.