广义线性模型拟似然估计的弱相合性
张 戈,吴黎军
(新疆大学数学与系统科学学院,乌鲁木齐 830046)
1 主要结果
广义线性模型(GLM)的理论是对线性模型的经典理论的重要推广,自从Nelder和Wedderburn[1]引入以来,已被广泛应用到许多领域。
设q×1维响应变量yi是相互独立的,协变量Xi是已知的p×q阶设计阵,yi服从指数分布:


其中
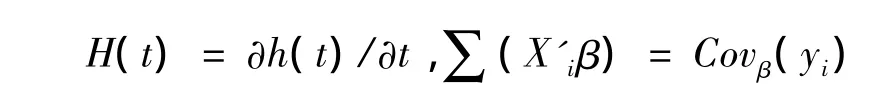
然而,在很多情形下,假定yi服从指数分布是不切实际的。事实上,只要均值函数假定正确,就可以预先假定响应变量的“工作分布”,进而用“工作方差”Λ(·)替换式(2)中的真实方差∑(·),并保留响应变量独立的假设,便可以得到拟似然方程:
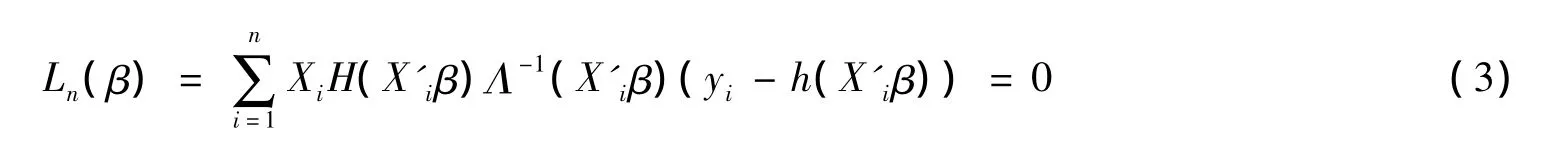
方程Ln(β)=0的根称作β0的拟极大似然估计。
关于广义线性模型的极大似然估计或极大拟似然估计的大样本性质在相关文献中已有不少讨论[1-4]。张三国,廖原[4]在假定误差方差有界的条件下研究了拟似然估计的弱相合性,但他们只讨论了典则联结的情形。本文在他们研究的基础上进一步推广到非典则联结情况下的弱相合性,并得到了与典则联结一样的结论,即的弱相合的必要条件。
本文所用到的c在不同的位置代表不同的正常数,‖·‖表示Euclid模,记{ei=yi-h(X'iβ0),i=1,…,n}为残差表示方阵的最大(小)特征值。
对一维响应变量,列出所需假设条件如下:
1)Xi有界;
2)对每个 t∈Rq,Λ(t)>0,det(t)≠0,Λ(t)一阶偏导连续,h(t)的二阶偏导连续;
4){ei}不含渐近退化子列;
主要结果表述为下面的2个定理:
定理1 若条件1)、2)、4)和5)成立,则可以得到如下收敛速度
2 定理的证明
引理1[5]假设独立随机变量序列{ξi,i≥1}不含渐近退化的子列。设cn1,…,cnn和bn为常数,使得当n→∞时,依概率有,则当 n → ∞ 时
定理1的证明

以不小于1-ε'n的概率成立。记
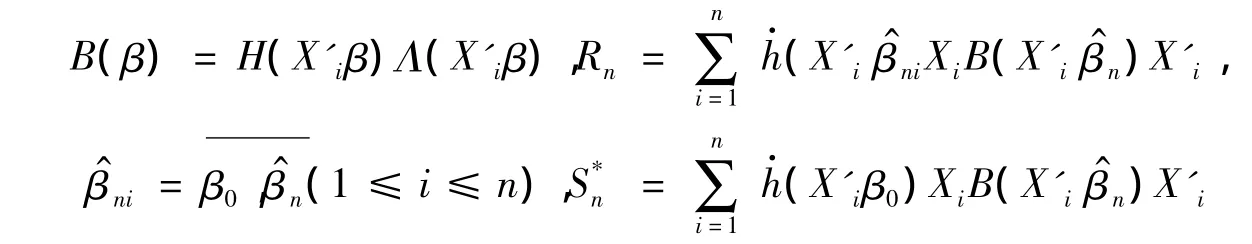
由式(4)以及引理1,存在常数序列ε″n↓0,使得
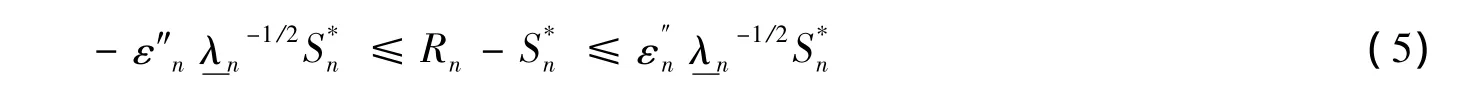
等价于
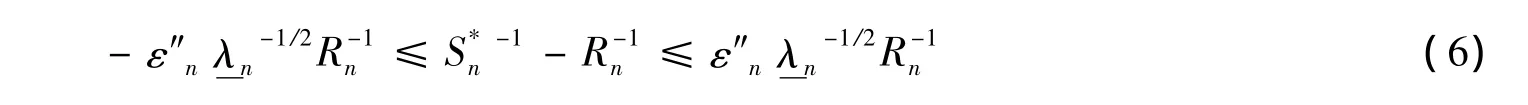
以不小于1-ε″n的概率成立,再由≤-1,有
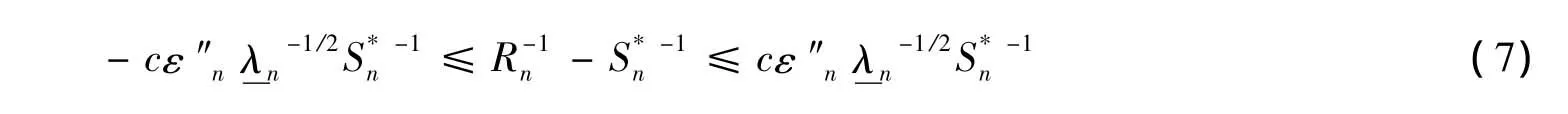
以不小于1-ε″n的概率成立,又由于对任意p维单位向量an,
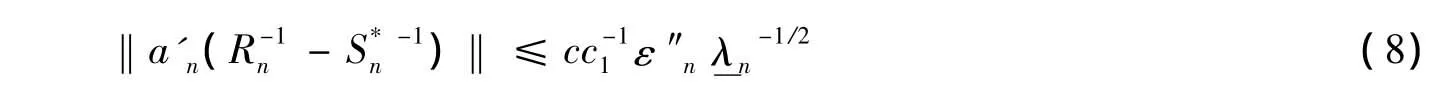
以不小于1-ε″n的概率成立。由式(8)、条件5)以及λmax()≤c2λn,可得

即
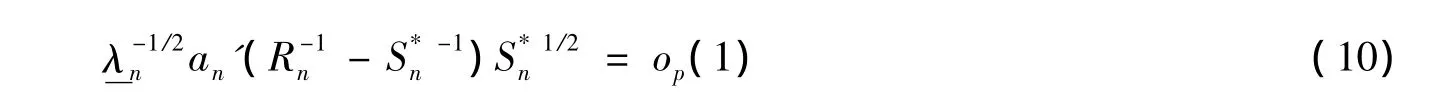
另一方面,记

由 Ln)=0 有
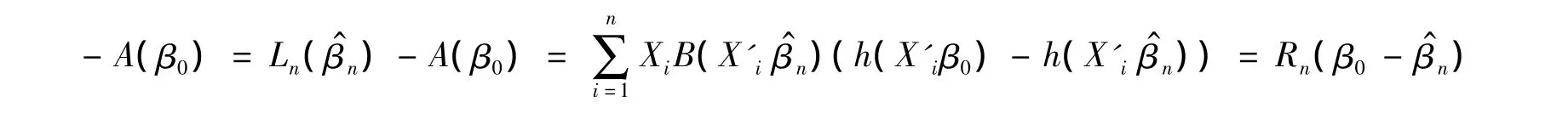
这样,对任意的p维单位向量an,
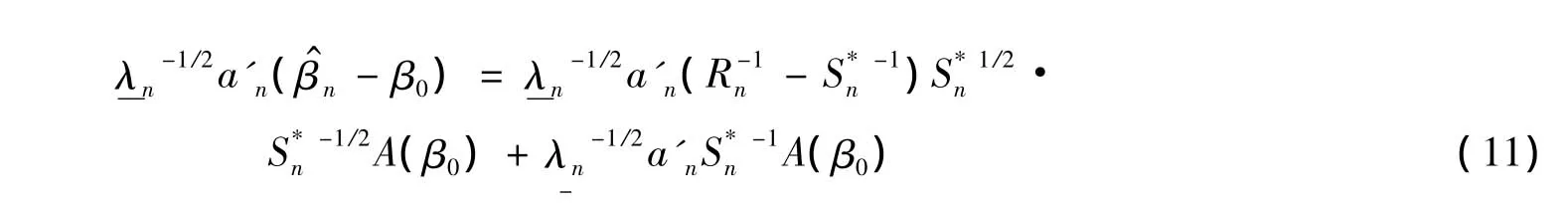
对任意依概率满足

的序列{an,n≥1},令这里序列{an,n≥1}的存在性由条件2)保证)。记
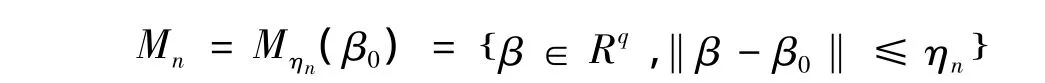
∂Mn表示Mn的边界。由于则有记从而
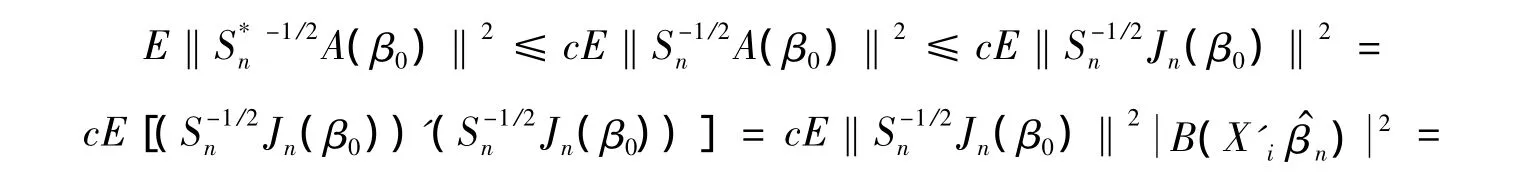

这说明

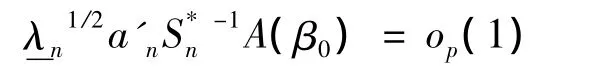
即,当n→∞时,依概率有
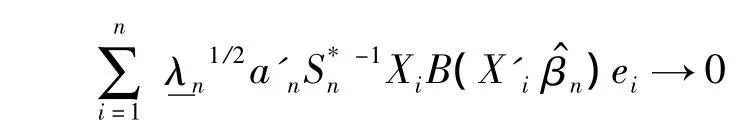
再由引理1,对任意单位向量an依概率有
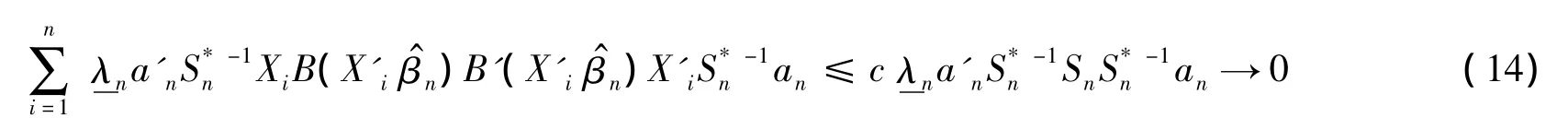
特别取an为对应特征值的单位向量,由于,有
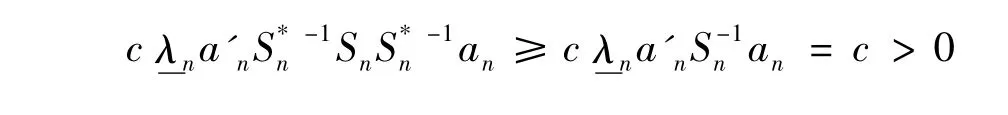
与式(14)矛盾。
引理2[4]对响应变量一维的线性回归模型yi=X'iγ0+ei,(1≤i≤n,n≥1),其中误差{ei}满足条件4,γ0的最小二乘估计为此处若单位向量a1,a2… 使得,则依概率有 a'n- γ0)→/0。
定理2的证明
矩阵Rn和的定义与定理1中的证明一样,有
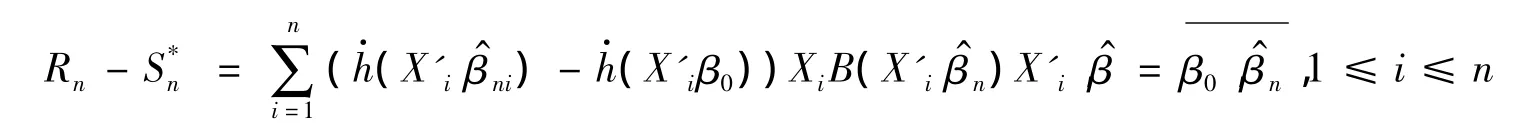

这样,当n充分大时,以概率1有
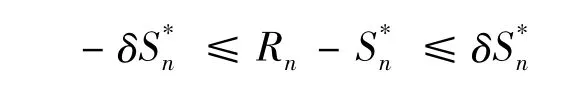
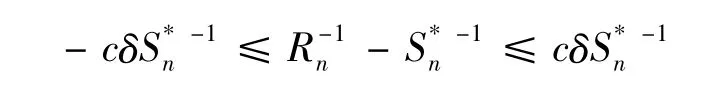
即
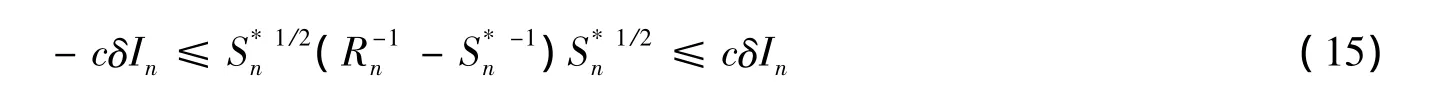

另一方面,



由式(16)得

[1]Nelder J A,Wedderburn R W M.Generalized linear model[J].J Roy Statist Soc Ser A,1972,135(3):370-384.
[2]Fahrmeir L,Kaufmann H.Consistency and asymptotic normality of the maximum likelihood estimator in generalized linear models[J].Ann Statist,11985,3(1):342-368.
[3]Yin C M,Zhao L C.Strong consistency of maximum quasi-likelihood estimate in generalized linear models[J].Sci China Ser-A-Math,2005,48(8):1009-1014.
[4]张三国,廖原.关于广义线性模型拟似然估计弱相合性的几个问题[J].中国科学A辑:数学,2007,37(11):1368-1376.
[5]陈希孺.线性模型参数的估计理论[M].北京:科学出版社,1985.

