基于均值-VaR-熵的证券投资组合应用研究

印凡成，陈瑞冰，黄健元

(河海大学 a.理学院;b.公共管理学院，南京 210098)

投资者将资金投放于有价证券市场都希望在一定的风险水平下获得较高的预期收益率，或预期收益率不低于某一期望值时投资风险能最小。一般情况下，有价证券的预期收益率越高，投资风险也就越大。但采用恰当的投资策略可以降低投资风险。实际上，证券组合投资就是一种降低投资风险的有效途径。1952年，马科维兹(Markowtz，H.M.)［1］提出均值 - 方差模型，奠定了现代证券投资组合理论的基础。该模型用方差度量风险，但是当投资者对于收益、风险理解不对称以及证券收益率不服从正态分布时，直接用方差度量风险会有很大的误差。随后很多学者提出了改进模型，其中一个主要途径是用新的风险指标代替方差建立模型，如:Young［2］提出的以投资组合最小顺序统计量作为风险函数的投资组合模型;Cai等［3］以投资组合各项资产收益中最大期望绝对偏差度量风险的投资组合模型。近年来VaR方法得到了广泛的关注和应用。国际上，三十人小组、美国证券交易委员会以及欧盟银行监管部门等［4］都将 VaR作为风险度量的标准。在国内，VaR方法也引起了金融机构和学者的关注。2002年，Alexander等［5］研究了允许卖空情况下的以VaR为风险函数的“均值-VaR”模型投资组合有效前沿。2005年，郭丹等［6］研究了机会约束下的均值-VaR组合投资问题。2008年，李宏杰［7］考虑证券投资组合过程中的交易费用，建立机会约束下的含资本结构因子和交易成本的均值-VaR模型。2010年，陈德秀、王建国［8］对均值-VaR分析下资产定价模型进行了拓展。经济全球化使得金融市场上风险与日俱增，采用新的更恰当的方法对金融风险进行监管，已成为各金融机构和金融当局的当务之急。

本文从证券投资组合理论的风险度量着手，基于熵可以作为不确定性度量指标，把熵作为VaR度量风险的一种有效补偿，以VaR和叉熵的线性组合为最小目标函数，预期收益率作为约束条件，并根据投资者对风险的具体厌恶程度对模型中各种备选证券的投资比例做出限定，构建考虑交易成本、不允许卖空的基于均值-VaR-熵的证券投资组合模型，并利用实际数据求得该模型的最优解及各资产的分配比例，证实该模型在我国金融风险监管中确实行之有效。

1 模型构建

假设有一种无风险证券和n种风险证券可供投资者选择，投资分为m期，第i种风险证券在t时的收益率为rti(t=1，2，…，m;i=1，2，…，n)，收益率的数学期望为ri(i=1，2，…，n)，则 ri=第i种风险证券的方差为(i=1，2，…，n)，第i种和第j种风险证券的协方差为σij，因此(rtj-rj)。假设每笔风险交易都有c倍的交易成本，无风险证券的收益率为。各风险证券占总投资的比重分别为xi(i=1，2，…，n)，无风险证券的投资比例为x0，显然各资产的投资比例之和要等于1，即可作为模型的一个约束条件。不允许卖空时有xi≥0(i=0，1，…，n)。投资者为了规避风险又可获得满意的收益，通常将无风险证券的投资比例设定在某一固定范围内，本研究设a≤x0≤b，其中0≤a≤b≤1。各风险证券的投资比例xi(i=1，2，…，n)的具体波动范围可根据投资者的风险厌恶程度进行设定，本研究假设ai≤xi≤bi(i=1，2，…，n)，其中 ai、bi为常数，且满足0≤ai≤bi≤1。对各证券投资比例xi的限定也是模型的约束条件，则投资组合的预期收益率和收益率的方差分别为

VaR指在正常的市场条件和给定的的置信水平α下，一定时期Δt内，投资组合最大的可能损失，数学表达式为:P(rp＜-VaR)≤1-α，其中α为置信水平，VaR为置信水平α下处于风险中的价值。

通常情况下，投资组合的收益率并不服从正态分布，可应用Bertsimas和Popescu的结论给出计算VaR值的严格形式［9］:，其中α∈(1/2，1]为置信水平。将投资组合的预期收益率和收益率的方差代入可得VaR的具体表达形式

常说的熵即信息熵，表示信息传输的平均不确定性，数学表达式为Sn(p1，p2，…，pn)=最小叉熵原理可表达为如下数学规划问题［10］:

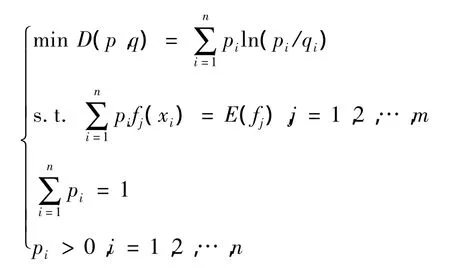
其中:p=(p1，p2，…，pn)为待求概率分布向量;q=(q1，q2，…，qn)为已知概率分布向量qi＞0，i=1，2，…，n);fj(j=1，2，…，m)为各阶统计矩函数;E(·)表示各阶统计矩的数学期望值;D(p，q)为叉熵函数，表示待求概率分布p到已知概率分布q的单向距离。

在一定的期望收益水平p下，即投资组合的期望收益率rp不低于p，也就是rp≥p，将前面给出的投资组合期望收益率的表达式代入上式可以得到模型的一个约束条件，即

下面对目标函数给出进一步说明:基于熵可以作为不确定性度量指标，本文把熵作为VaR度量风险的一种有效补偿，以收益率服从非正态分布假设下严格形式的VaR和叉熵函数的线性组合来度量风险，即目标函数为

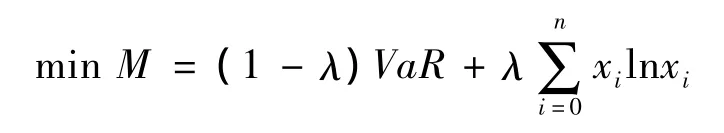
将VaR具体形式代入，目标函数表达式为

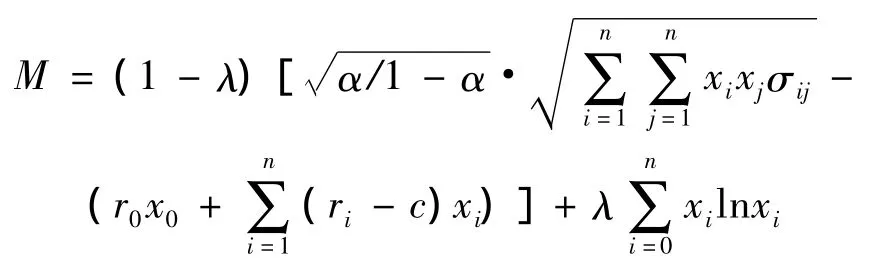
其中0≤λ≤1为调节参数，根据风险偏好决定。

如果仅考虑投资组合的期望收益率在既定水平下投资风险最小，则由上面的分析可知，在收益率服从非正态分布假设下构建考虑交易成本、不允许卖空的基于均值-VaR-熵的证券投资组合模型如下:

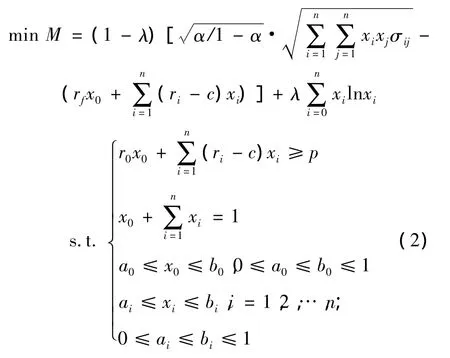
该模型的意义在于:通过确定适当的组合证券的投资比例，可以使得证券组合投资的预期收益率和投资风险都达到投资者的要求。这一结论不仅对于一般散户投资者的投资决策具有一定的指导意义，而且对于大规模的投资决策尤其机构投资者也有着非常重要的意义。

2 实例分析

设某投资者选择 A、B、C、D、E五只股票和一种无风险证券F进行投资。其中无风险证券F的日收益率r0=0.25%，投资比例设定在10%≤x0≤45%。B股票的投资比例为0.5%≤x2≤5%，D股票的投资比例为0.3%≤x4≤2.5%，其他3只股票的投资比例不做限制。调节参数取λ=0.01，另设风险资产交易费用率c=0.007 5，设收益率服从非正态分布假设下的均值-VaR-熵模型的置信水平为95%。已知A、B、C、D、E五只股票2010年5月至10月101个交易日的日收盘价，可计算5只股票各自的日收益率均值和方差，如表1所示，5只股票日收益率的协方差如表2所示。

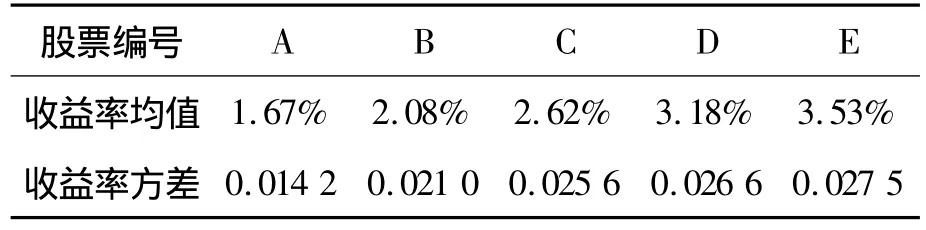
表1 5只股票2010年5月至10月日收益率均值及方差

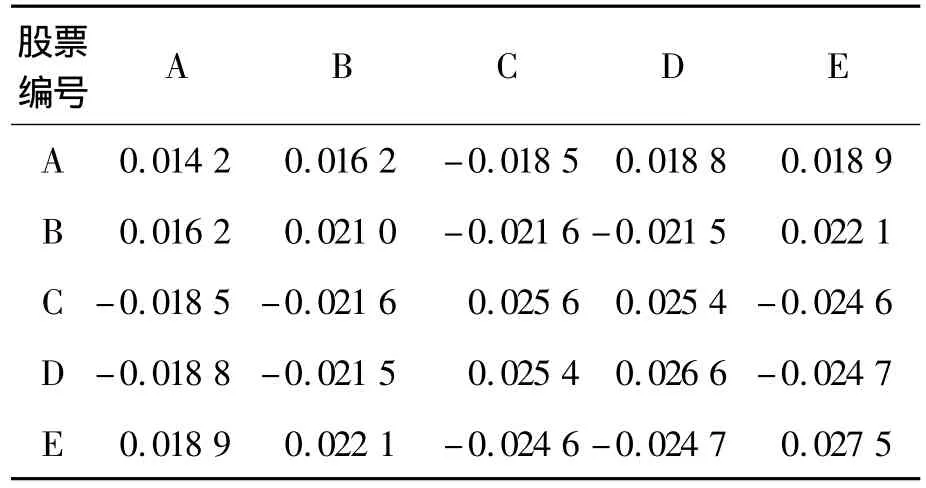
表2 5只股票2010年5月至10月日收益率协方差

由表1可知五只股票日收益率均值的最大值为3.53%，最小值为1.67%，而无风险证券F的日收益率为0.25%，低于5只股票日收益率均值的最小值，由投资比例的非负性和归一性［11］可知min{ r0，rmin}≤p≤rmax，即:0.25%≤p≤3.53%。

此处投资者能接受的投资组合最小期望收益率p取值为2.0%时，将数据代入前面建立的均值-VaR-熵模型，用Matlab软件编程进行求解非线性最优化问题，可得具体投资比例，见表3。

表3 收益率服从非正态分布假设下均值-VaR模型求解结果

也就是说，在满足收益要求及投资限制条件下，各证券投资比例为:当X=(0.282 8，0.043 3，0.102 6，0.025 0，0.446 3，0.100 0)T时，模型目标函数取得最小值，也就是最小风险M=0.376 5。由模型的最优投资组合的求解可知，投资者会权衡风险和收益，在满足预期收益的前提下选择使得投资风险最小的组合来投资。此处的均值-VaR-熵模型考虑了投资者的风险厌恶程度，相对均值-方差模型来说更具有现实意义。

3 结束语

无论机构还是个人投资者进行投资时，都应充分考虑可选择的投资工具及风险收益特征，尽量采取多元化投资来保证收益或规避风险，并注重投资组合的科学性、合理性及有效性。不同于Markowitz的均值-方差模型，本文从证券投资组合理论的风险度量着手，基于熵可以作为不确定性度量指标，把熵作为VaR度量风险的一种有效补偿，以VaR和叉熵函数的线性组合为最小目标函数，预期收益率作为约束条件，并根据投资者对风险的具体厌恶程度对模型中各种备选证券的投资比例做出限定，构建考虑交易成本、引入无风险证券投资、不允许卖空、收益率服从非正态分布的基于均值-VaR-熵的证券投资组合模型，并利用实际数据求得该模型的最优解及各资产的分配比例，是将VaR方法和熵函数应用于现实金融市场风险管理中的一次有益尝试。

［1］MARKOWITZ H.Portfolio selection［J］.Journal of Finance，1952，7:77-91.

［2］YOUNG M R.A minimax portfolio selection rule with linear programming solution［J］.Management Science，1998，44:673-683.

［3］CAI X Q，TEO K L，Yan X Q，et al.Portfolio optimization under a minimax rule［J］.Management Science，2000，46:957-972.

［4］张慧毅，徐荣贞，蒋玉洁.VaR模型及其在金融风险管理中的应用［J］.价值工程，2006，8:61-63.

［5］ALEXANDER G，BATISTA A.Economic implication of using a mean-VaR model for portfolio selection:A comparison with mean-variance analysis［J］.Journal of Dynamics ＆ control，2002，26:1159-1193.

［6］郭丹，徐伟，雷佑明.机会约束下的均值-VaR组合投资问题［J］.系统工程学报，2005，20(3):256-260.

［7］李宏杰.机会约束下的含有资本结构因子和交易成本的均值-VaR投资组合模型［J］.中国管理科学，2008，16(3):31-36.

［8］陈德秀，王建国.均值-VaR分析下的资产定价模型的拓展［J］.商业经济，2010(7):37-38.

［9］LAURENT E G，MAKSIM O，Francois O.Worst-case value-at-risk and robust portfolio optimization:A conic programming approach［J］.Operation Research，2003，15(4):543-556.

［10］李华，李兴斯.证券投资组合中的熵优化模型研究［J］.大连理工大学学报，2005，45(1):153-156.

［11］郁志勤.投资组合优化模型分析与算法实现［D］.上海:上海交通大学，2010.