半参数部分线性模型在小麦抗倒伏性分析中的应用
刘 锋,徐振枢,王利兵
(重庆理工大学数学与统计学院,重庆 400054)
小麦的机械强度受到小麦许多指标因素的影响,其中,小麦抗倒伏性对小麦生产至关重要[1-3]。小麦的抗倒伏性在小麦生长的不同时期可造成不同的影响。通过增强小麦的抗倒伏指数,可以更有效地让小麦成熟,从而增加小麦产量。本文主要用部分线性模型对小麦机械强度与小麦各参数之间的关系进行研究。
1 部分线性模型与拟合方法
1.1 部分线性模型
Engle(1986)[4]首先提出了半参数部分线性模型,其具体形式是:
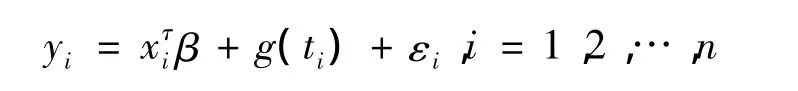
其中:x=(x1,x2,…,xs)是随机变量;xj,j=1,2,…,s是x的第j个分量;β是未知参数部分;g(·)是未知函数部分;ε为随机误差,随机误差部分需要满足E(εi)=0,Var(εi)=σ2。本文就是要应用部分线性模型得到小麦抗倒伏指标中机械强度与小麦自身的指数之间的参数关系,进而进行分析。
1.2 两步估计算法
对于上述的部分线性模型,需要对未知参数和未知函数部分进行估计。本文应用两步估计算法对未知的函数进行估值,从而得到函数的形式。两步估计算法[5]是通过将函数拟合得到对于未知部分的估计值。
模型为

对于该模型以变量T取条件期望,从而得到方程:
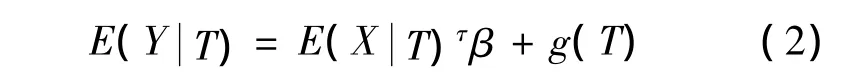
式(2)减去式(1)得到:
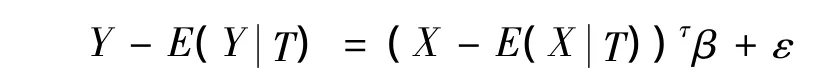
1.3 缺失数据分析
缺失数据是在生活与科研中经常遇到的,由于部分原因导致了数据统计中出现了数据的缺失,进行分析时只能对一部分数据进行分析。
对于缺失数据的分析,首先设定缺失指示变量,即:

据此可以得出相应的缺失模型:
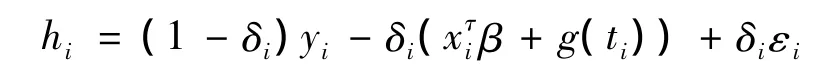
利用已知数据及上述模型,根据文献[6]得到缺失数据的借补值。
2 数据与实证分析
2.1 数据的选取
本研究选取了2007、2008和2011年小麦数据(矮抗58,周麦18),包括小麦各节长度、粗度,单个小麦的重心高度、茎秆壁厚、穗重等对小麦抗倒伏性研究较为重要的指标。

可以看到,上述公式中茎秆鲜重与茎秆重心高度都可以通过测量得到,而机械强度往往不容易获得,因此茎秆机械强度对于小麦抗倒伏性是非常重要的。
由于只有2007年的数据给出了具体的小麦机械强度测量数据,因此首先就要进行数据分析和方程拟合,得到机械强度与各指标之间的函数关系,进而应用2008年与2011年的数据得到这2个年度小麦品种的机械强度。通过3个年度的数据比较,分析出矮抗58的抗倒性要强于周麦18的抗倒性。
2.2 数据分析
2.1.1 周麦18分析
在2个小麦品种之中,周麦18这个小麦品种的各项指标不存在缺失,因此先分析该种小麦。
令:y为机械强度;x1为茎秆重心;x2为基部第5节长度;x3为基部第5节粗度;x4为基部第4节长度;x5为基部第4节粗度;x6为基部第3节长度;x7为基部第3节粗度;x8为基部第2节长度;x9为基部第2节粗度;x10为茎秆壁厚;x11为麦穗鲜重。
首先通过数据的相关性分析得到机械强度与主要指标之间的相关系数矩阵,见表1。
对小麦品种周麦18进行因子分析,结果表明,前2个成分的累积贡献率达到0.801 56,因此取这2个成分进行分析。具体形式为:


由图1、2可以看出:第1成分与机械强度之间存在着较强的线性关系,而第2成分与响应变量之间无法得到具体的函数形式。因此,用部分线性模型进行拟合,核函数选取为k(t)=15×(1-t2)2/16,窗宽选择为h=0.911 423 5,利用两步估计,得到拟合方程为


图1 周麦18第1成分与机械强度之间的关系
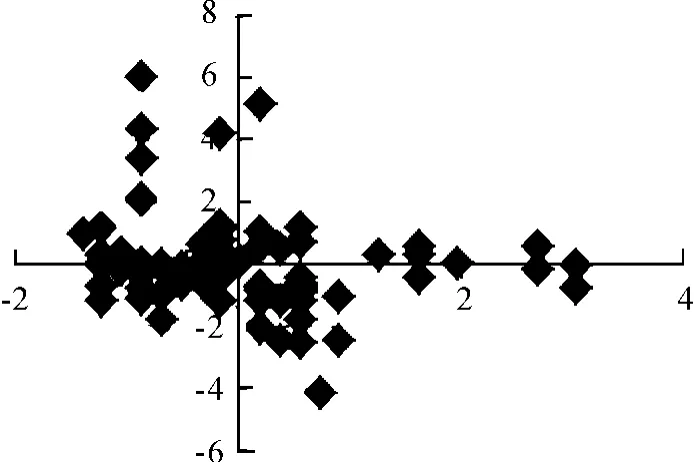
图2 周麦18第2成分与机械强度之间的关系
2.1.2 矮抗58分析
矮抗58的数据存在缺失,并且存在个别的异常数据。首先要对数据进行筛选,同时对缺失数据进行借补。将借补值填充到缺失值对应的部分进行分析。首先对机械强度与小麦各指标数据之间进行了相关系数分析,对数据进行标准化,得到矮抗58机械强度与主要指标之间的相关系数矩阵,见表2。

表2 矮抗58机械强度与主要指标之间的相关系数矩阵
通过因子分析得到对于矮抗58这个小麦品种机械强度与各个品种之间的关系。通过数据模拟可以得到前2个成分的累积贡献率达到0.820 29,因此取这2个成分进行分析,其具体形式为:

接下来将得到的2个成分与小麦机械强度作散点图,见图3、4。
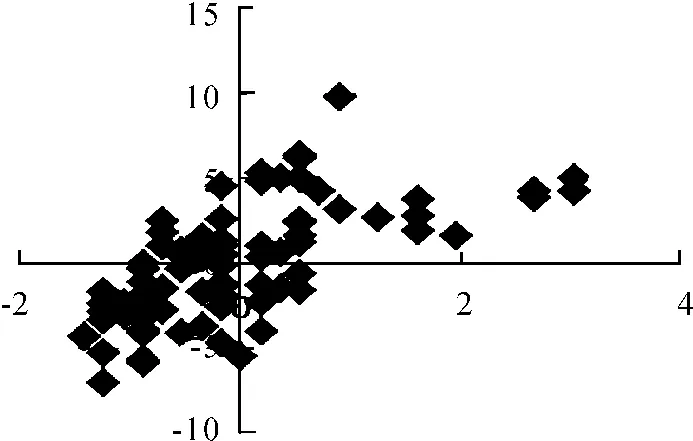
图3 短抗58第1成分与机械强度之间的关系
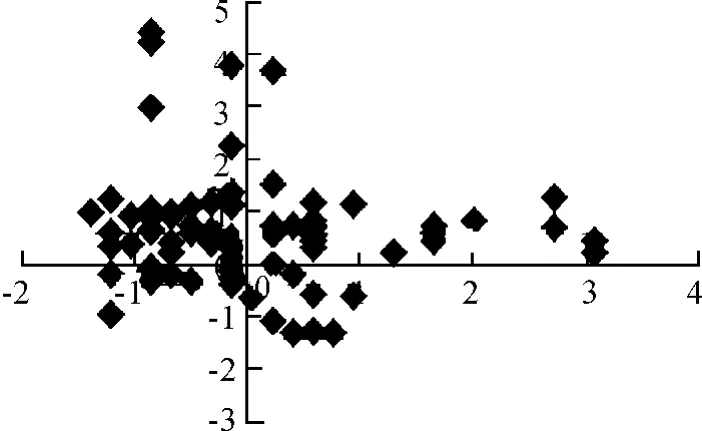
图4 短抗58第2成分与机械强度之间的关系
由图3、4可以看出,小麦机械强度与第1成分有较为明显的线性关系,而第2成分与小麦机械强度之间得不到具体的函数形式。核函数选取为k(t)=15×(1-t2)2/16,窗宽选择为h=1.322 978,利用两步估计,得到拟合方程为
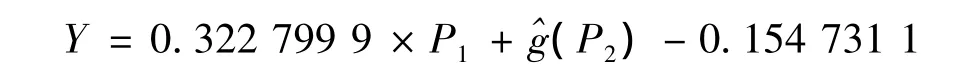
将利用上述方法得到的模型应用到2007、2008年与2011年的数据之中,分别计算出2个小麦品种在这2个年度中样品的机械强度。加上2007年数据,结果见表3。
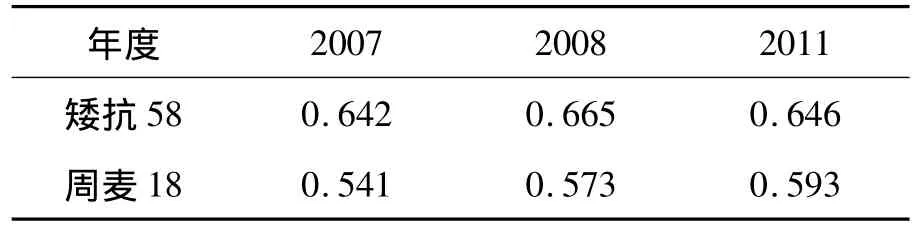
表3 3个年度2个小麦品种机械强度 kg
3 结束语
部分线性模型理论正在逐步推广,其应用还不是很全面。部分线性模型是一种非参数模型,许多统计问题可以应用该模型进行求解。两步估计算法在部分线性模型的估计中起到了举足轻重的作用,它可以有效解决部分线性模型各个函数的估计问题,如本文中所应用的方法可以有效地解决“维数灾祸”的问题。
本文将部分线性模型应用到小麦抗倒伏性的研究中,获得了对小麦抗倒伏性起到关键作用的机械强度指标的计算方法,得到了所给定的小麦品种之中矮抗58的小麦抗倒伏性最强的结果。但由于数据给定的范围较为有限,模型的精度还有待进一步的提高,还需要进一步研究。
[1]田保明,杨光圣,曹刚强.农作物倒伏及其影响因素分析[J].中国农学通报,2006,22(4):163-167.
[2]王勇,李斯深,李安飞,等.小麦种植抗倒性的评价和抗倒性装的相关与通径分析[J].西北植物学报,2000,20(1):79-85.
[3]余泽高,李志新,严波.小麦茎秆机械强度与若干形状的相关性研究[J].农业工程学报,2007,23(7):14-18.
[4]Engle R F,Granger C W J,Rice J,et al.Semiparametric estimates between weather and electricity sales[J].Journal of American Statistical Association,1986,80:310-319.
[5]封维波,刘琼荪.半参数模型中两步估计与最小二乘估计的比较[J].统计与决策,2008(4):27-29.
[6]杨宜平,薛柳根,程维虎.响应变量存在缺失时部分线性模型的经验似然[J].高校应用数学学报,2010,25(1):43-52.

