一类非自治混沌系统的自适应时滞反馈同步控制
叶志勇,吴 用,刘 原
(重庆理工大学数学与统计学院,重庆 400054)
混沌控制与同步是目前非线性科学研究的一个重要内容。近几十年,混沌系统的控制与同步吸引了很多专家学者的重点关注。经过科学家们努力的研究,多种研究混沌控制的方法被提出来了,如自适应同步控制法[1-4]、参数变分控制法、状态反馈控制法、时滞反馈控制法[5-8]、最优控制法、鲁棒控制法等,这些方法已被应用到了信息科学、医学、生物等领域,并且取得了很多的成果。到目前为止,混沌控制的研究都集中非时滞和时滞的反馈控制这2个方面[9-10]。由于控制系统中考虑时滞会使得证明的过程具有一定的复杂性,所以对含时滞的研究还比较少。然而,在实际的应用中,时滞现象是普遍存在的,因此不能忽视。本文提出了一种n维非自治系统自适应时滞反馈控制的方法,通过选取一个合适的自适应反馈控制器,构造特殊形式的Lyapunov函数,给出了一类非自治混沌系统的全局自适应同步的判据。最后把理论的结果应用于有名的杜芬振子,用数值模拟验证结论的正确性。
1 问题的提出
1.1 预备知识
1)A>0表示A为正定矩阵,A≥0表示A为半正定矩阵。
2)λmax(A)表示矩阵A的最大特征值,λmin(A)表示矩阵A的最小特征值。
5)引理1(Barbalat’s Lemma)[11-12]假设函数f(t)是一个一致连续函数存在且有界,因此当t→+∞时,f(t)→0。
6)定义1 Lip(G)指一类含有利普希茨常数G的利普希茨连续函数。
7)定义 2[13]令 P=diag{ pp…,p}是一个正定的对角矩阵,Δ =diag{ δ,δ,…,δ}是一个对角矩1,2,n12n阵。QUAD(Δ,P)指一类连续函数 f(t,x):[0,+∞)× Rn→Rn满足:对某一个 ε >0,所有的 x,y∈Rn和t>0,有(x-y)TP {[f(t,x)-f(t,y )]-Δ[ x-y]}≤-ε(x-y)T(x-y)成立。
1.2 数学模型及控制器设计
给定n维非自治混沌系统:

其中:x(t)∈Rn,x(t)=(x1(t),x2(t),…,xn(t))T是系统(1)的状态变量;A为n阶常数方阵;f(t,x)为[0,+∞)×Rn→Rn的非线性连续函数;f(t,x)是一个非线性函数。
现在考虑主系统具有方程(1)这样的表达式,且主系统是一个混沌系统。再给出一个从系统的表达式:
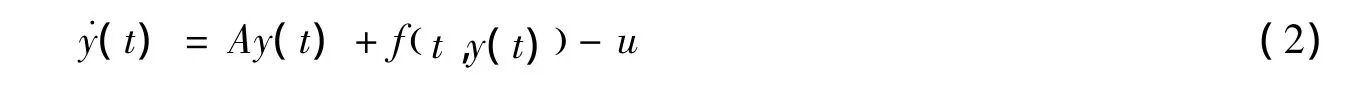
其中:y(t)=y1(t),y2(t),…,yn(t)是从系统的状态变量;u是一个时滞自适应控制器;τ>0为常数时滞;A为n阶常数方阵。
研究的目标就是给从系统(2)设计一个合适的控制器,使得从系统(2)能和主系统(1)达到同步。
2 混沌系统的同步

令时滞自适控制器为这里的增益函数矩阵 K(t)=diag{k1(t),k2(t),…,kn(t)},P=diag{ p1,p2,…,pn}是一个正定的对角矩阵,e(t)=y(t)-x(t),e(t-τ)=y(t-τ)-x(t-τ)分别为主系统(1)和从系统(2)的不含时滞同步误差和含时滞的同步误差。假设存在n个正常数使得是一个正定的对角矩阵,则有以下定理:
定理1 令控制器u=K(t)(2e(t)-e(t-τ)),这里的增益函数矩阵为K(t)=diag{k1(t),k2(t),…,kn(t)},且为同步误差,θi(i=1,2,…,n)为任意的正常数,且f(t,x)∈QUAD(Δ,P)。假设存在n个正常数使得,且是一个正定的对角矩阵,使得H=(PA)s+PΔ-εIn-K*为负定矩阵,那么从系统(2)能和主系统(1)达到同步。
证明 通过主系统(1)和从系统(2)做差,可以得到
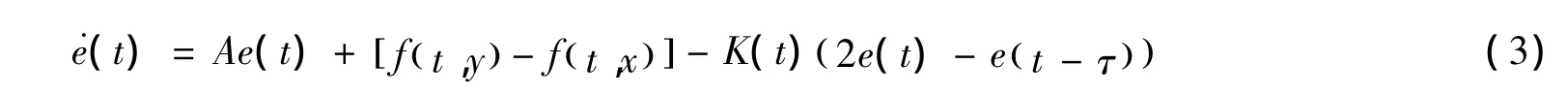
这里的 e(t)=e1(t),e2(t),…,en(t)T。
构造李雅普洛夫函数
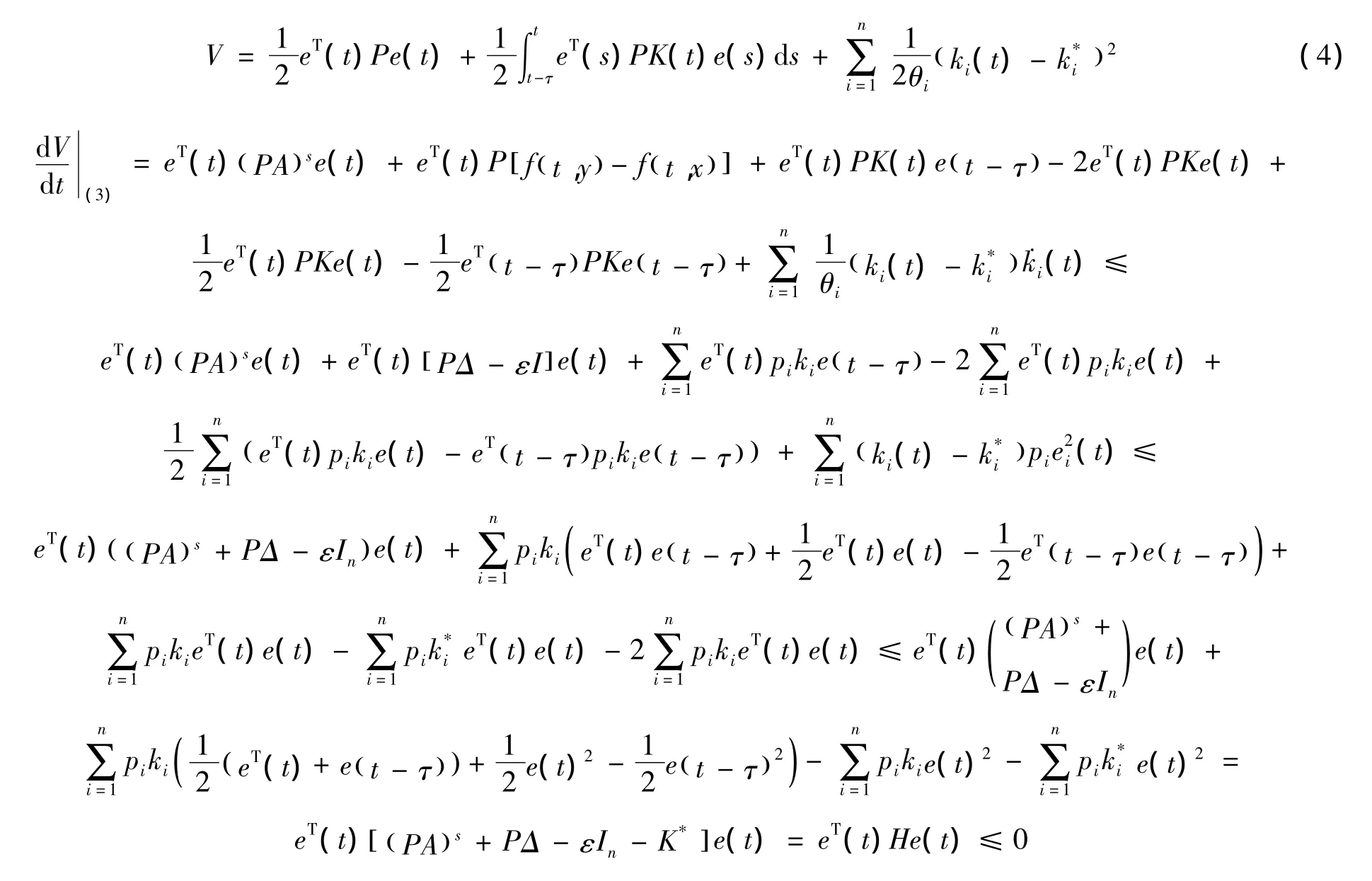
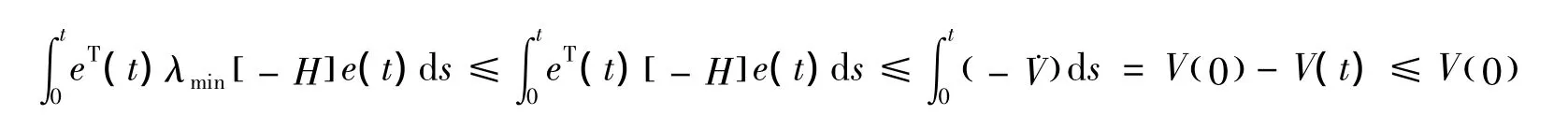
通过引理可知:当t→+∞时,ei(t)→0,i=1,2,3…n。因此,从系统(2)和主系统(1)达到了同步,定理1证明完毕。
推论 1 如果 f(t,x)为[0,+∞)×Rn→Rn的非线性连续函数,且f(t,x(t))=(f1(t,x1(t)),…,f(t,xn(t)))T∈Rn,则满足fi(t,xi(t))∈Lip(Gi),i=1,…,n,这里利普希茨常数 Gi>0。假设存在n个正常数使得,且H=PA+Gi-K*为负定矩阵,则从系统(2)和主系统(1)达到同步。
推论1的证明的方法和定理1的证明方法相同,因此省略。
3 数值模拟
例1 考虑杜芬振子[13]:

把主系统变为

取参数a=0.1,r=10,ω=1,数值模拟得到系统(7)的解轨线产生的混沌吸引子相图如图1所示。
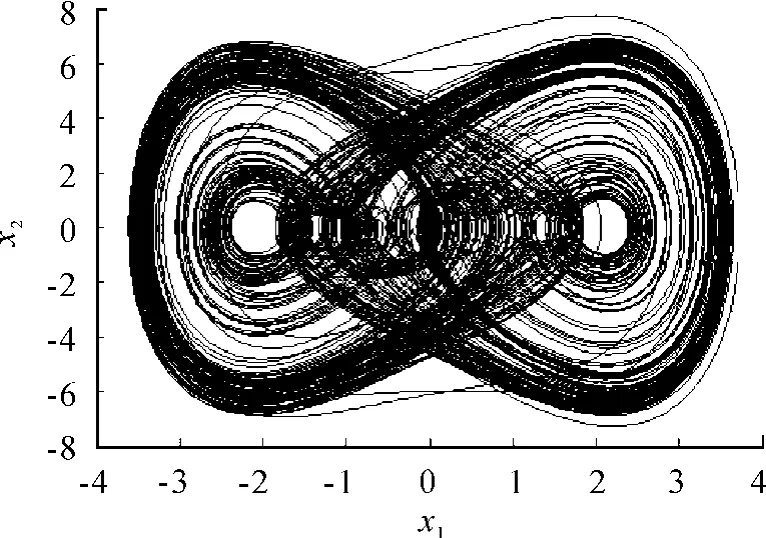
图1 杜芬振子产生的混沌吸引子相图
考虑从系统
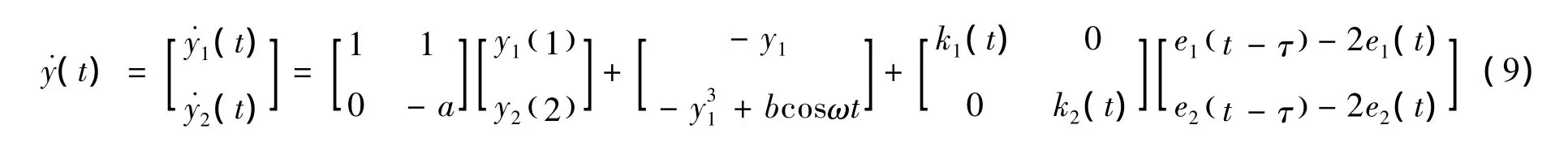
其中
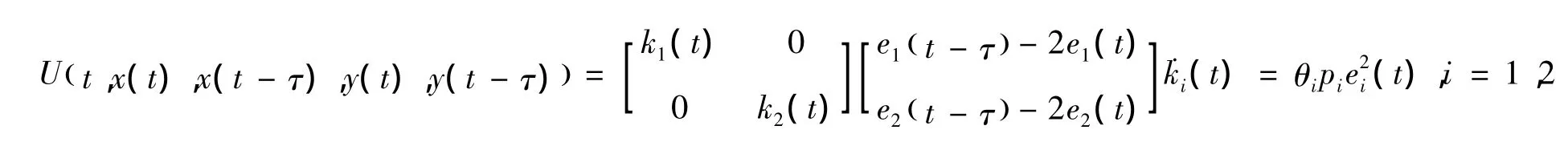
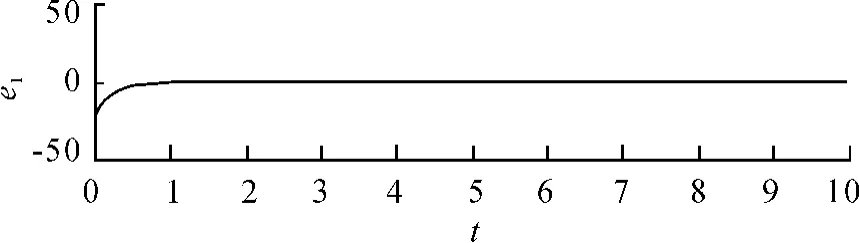
图2 杜芬振子同步误差e1的稳定状态
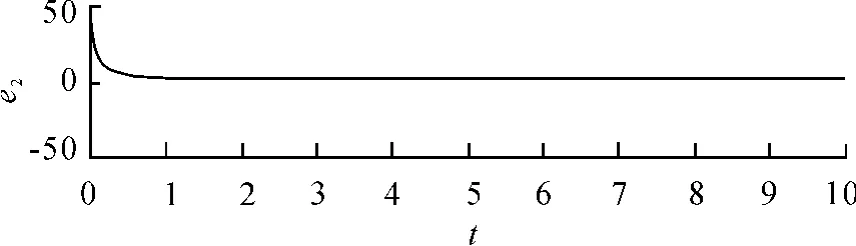
图3 杜芬振子同步误差e2的稳定状态
4 结束语
本文提出了一种n维非自治系统自适应时滞反馈控制的方法。运用此方法,确定了一个满足一定条件的主系统,只要选择一个合适的控制器,就能让主从系统达到全局渐进同步。该方法的优点在于控制器含有时滞。最后用数值模拟验证了结论的正确性。
[1]Gonzalez G A.Controlling chaos of an uncertain Lozi system via adaptive techniques[J].Int J Bifur Chaos,1994,4:559-562.
[2]Bernardo M.An adaptive approach to the control and synchronization of continuous-time chaotic systems[J].Int J Bifur.Chaos,1996,6:557-568.
[3]Cao Y J.A nonlinear adaptive approach to controlling chaotic oscillators[J].Phys Lett A,2000,270:171-176.
[4]Wu X Q,Lu J A.Adaptive control of uncertain Lii system[J].Chaos,Solitons and Fractals,2004,22:375-381.
[5]Bleich M E,Socolar J E S.Stability of periodic orbits controlled by time-delay feedback[J],Phys Lett A,1996,210:87-94.
[6]Nakajima H.On analytical properties of delayed feedback control of chaos[J].Phys Lett A,1997,232:207-210.
[7]Chen G,Yu X.On time delayed feedback control of chaotic systems[J].IEEE Trans on Circu Syst,1999,46:767-772.
[8]罗晓曙,方锦清,孔令江,等.一种基于系统变量延迟反馈的控制混沌方法〔J].物理学报,2000,49:1423-1427.
[9]Gopalsamy K.Stability and Oscillations in Delay Differential Equations of population Dynamics[M].USA:Kluwer Academic Publishers,1992.
[10]叶志勇,邓存兵,江华南.非自治混沌系统中时滞的反馈控制和应用[J].重庆理工大学学报:自然科学版,2011(1):85-90.
[11]胥红星.一个简化Lorenz混沌系统的全局吸引集及应用[J].四川兵工学报,2011(7):143-146.
[12]Wang X Y,Meng J.Generalized synchronization of hyperchaos systems[J].Acta Phy Sinica,2007,56:6288-6293.
[13]Ueda Y.Steady motions exhibited by Duffing’s equation:a picture book of regular and chaotic motions[C]//Holmes P J.New Approaches to Nonlinear Problems in Dynamics.SIAM,Philadelphia:[s.n.],1980.

