一类二阶时滞微分方程脉冲解的存在性与指数稳定性

王宗毅

(惠州学院数学系，广东惠州516007)

1 引言与预备知识

很多数学模型都可以用时滞微分方程来研究，其中一个重要的方面即是方程解的存在性与稳定性研究，以及在适当脉冲条件下解的指数稳定性研究，后者在控制理论、种群动力学、物理和化学等领域应用广泛［1－5］. GIMENS 和FEDERSON［6］研究了如下方程

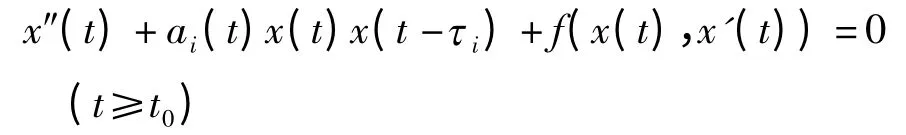
的解的稳定性. 本文推广了文献［6］的结果，研究如下一类二阶时滞微分方程

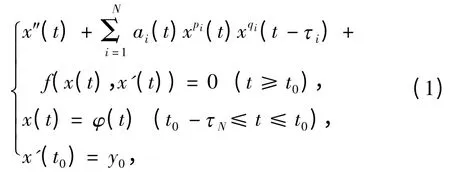
其中0≤τ1＜τ2＜…＜τN，fC(R2，R)，存在常数F使对任意(x，y)R2成立，f(0，0)=0，ai为［t0，+∞)→R 上的右连续有界函数，pi+qi=1，0≤pi，qi≤1 (i=1，…，N).

令［a，b］⊂R，K⊂(a，b)且K 是有限的.C(［a，b］，R)是由［a，b］→R 的连续函数组成的Banach 空间且定义上确界为范数，即定义C1(［a，b］，R)为［a，b］→R 的一阶连续可导的函数组成的空间，赋予范数:

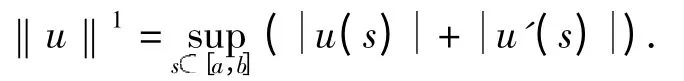
易知C1(［a，b］，R)为Banach 空间. 令(［a，b］，R)为［a，b］K 上一阶连续可导函数组成的空间，对任意(［a，b］，R)，x，x'在t =c (∀cK)处均存在单侧极限且为右连续.

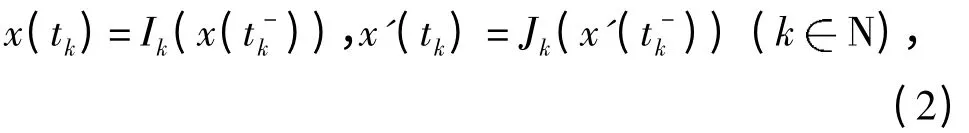
其中Ⅰk，JkC(R，R)且Ⅰk(0)=Jk(0)=0. 易知x≡0 为方程(1)的平凡解. 设有以下假设:

(H1)φ(t)和φ'(t)至多除了有限多个点外在［t0－τN，t0］上连续，在这有限点处的单侧极限φ'(t－)，φ'(t+)存在且φ 和φ'均是右连续的;

(H2)‖·‖取函数在［tk，tk+1］的上确界范数;

(H3)存在常数ck和dk，使得对任意xR 成立.

定义1［7］称函数x(t):R→R 为方程(1)和条件(2)过点(t0，φ，y0)的一个解，若x(t)满足:

(i)x(t)，x'(t)在［t0，+ ∞){tk:kN}上连续，且在{tk，kN}上存在单侧极限且右连续;

定义2［7］方程(1)被称为在条件(2)下脉冲指数稳定是指，若存在α ＞0 和一串单调递增序列{tk}kN，使得对任意ε ＞0，存在δ ＞0，解x(t;t0;y0)满足则

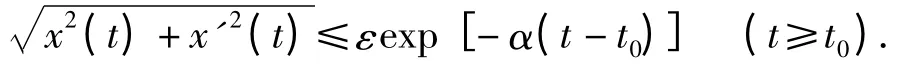
引理1［8］(Schaefer 不动点定理)设S 为一线性赋范空间，F:S→S 为列紧集. 定义:H(F)={xS:x=μF(x)，μ(0，1)}，则以下结论之一成立:

(i)集合H(F)为无界集;

(ii)F 在S 上有不动点.

2 主要结果

定理1 设条件(H1)～(H3)成立，则方程(1)和条件(2)存在定义在［t0－τN，+∞)上的一个解.

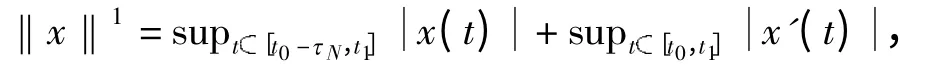
易见其为Banach 空间. 定义算子N0:(［t0－τN，t1］，R)→(［t0－τN，t1］，R)，

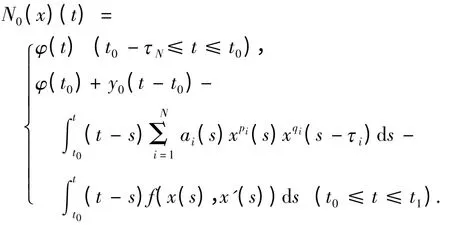
下面分步证明N0在［t0－τN，t1］上存在不动点. 如下性质成立:

(1)N0是连续的. 令R)，则在(［t0－τN，t1］，R)中xn收敛到x(n →∞)意味着即，xn→x，x'n→x'在区间［t0，t1］上为一致收敛，则

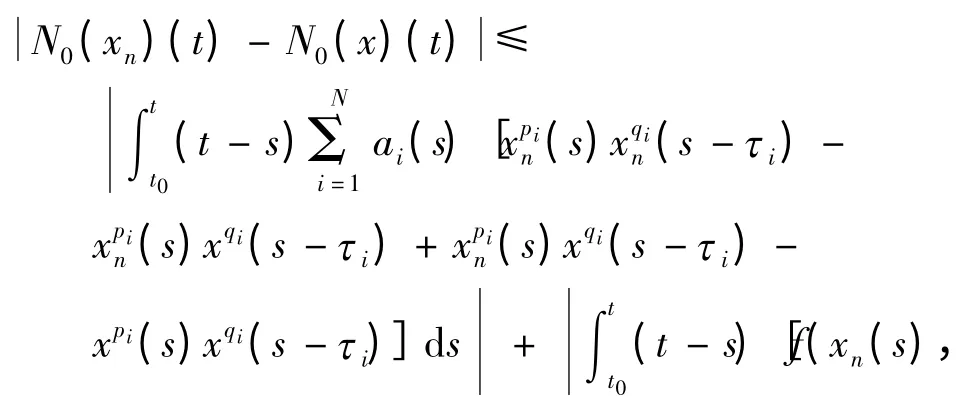
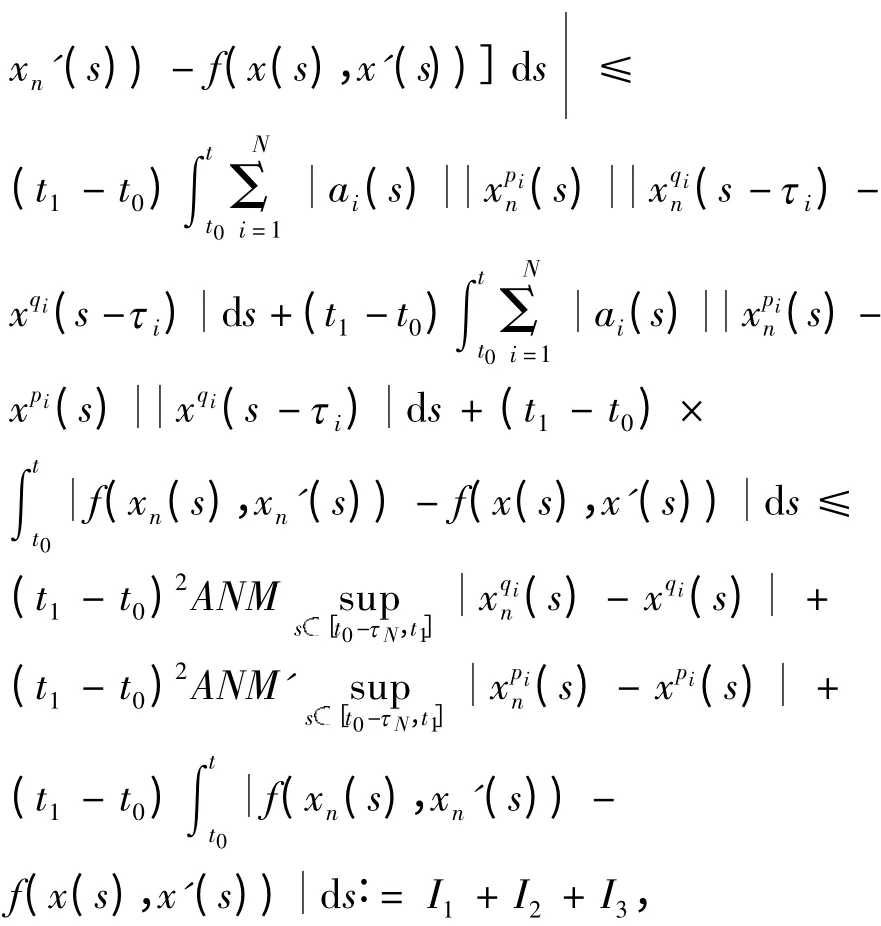
其中M=max{‖xn(s)‖pi，nN}，M'=max{‖x(s)‖qi，nN}，易见Ⅰ1，Ⅰ2趋于0 当xn→x. 由f 连续性和Lebesgue 控制收敛定理可知Ⅰ3趋向于0，即

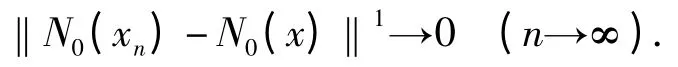
(2)N0把有界集映到有界集.对任意给定的p≥0，xBp:={y(［t0－τN，t1］，R);‖y‖≤P}，有

(3)N0在(［t0－τN，t1］，R)中把有界集映到等度连续集.令l1，l2［t0，t1］且l1＜l2，对每个x，有

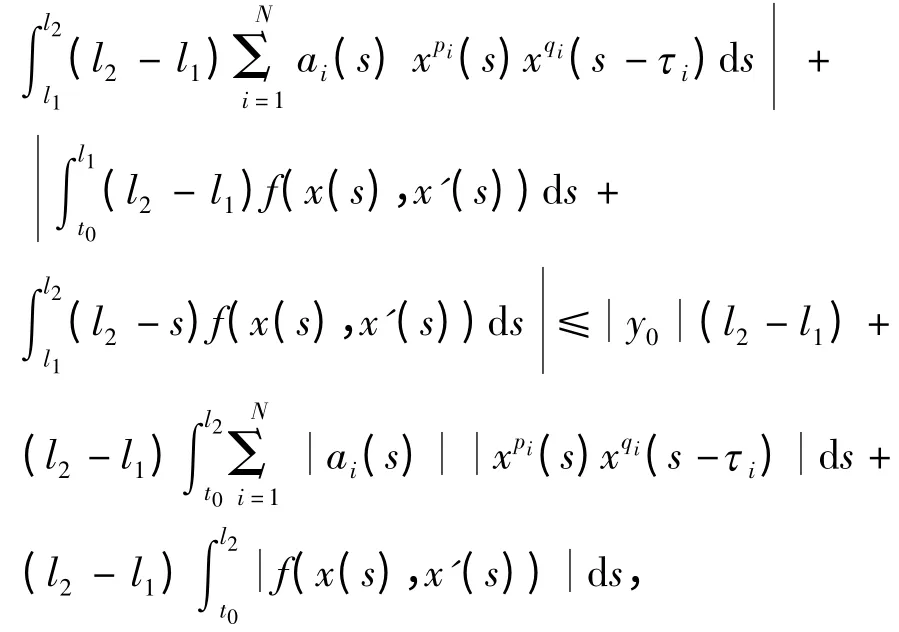
上式趋向于0 当l2→l1. 同理可证若l1＜l2≤0 或l1≤0≤l2等度连续性亦成立.

由性质(1)～(3)知N0(Bp)是有界和等度连续映射，根据Ascoli－Arzela 定理知N0(Bp)是列紧的.

(4)集合Λ(N0)={x(［t0－τN，t1］，R):x =λ N0(x)，0 ＜λ ＜1}是有界的.

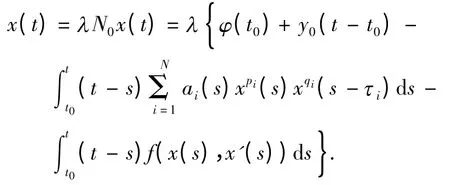
根据性质(2)和0 ＜λ ＜1，得

于是

故Λ(N0)是有界的.

由性质(1)～(4)和Schaefer 不动点定理，可知N0有一个不动点y1(t). 则

为方程(1)和条件(2)在区间［t0－τN，t1)上的一个解.

考虑问题

定义算子N1(［t1-τ，t2］，R)为

其中K1= φ ∪{t1}.我们需证N1在区间［t1-τN，t2］上存在不动点. 由定义知N1可表示为

由性质(1)～(4)的证明过程易知N1存在一个不动点，设为y2(t). 则

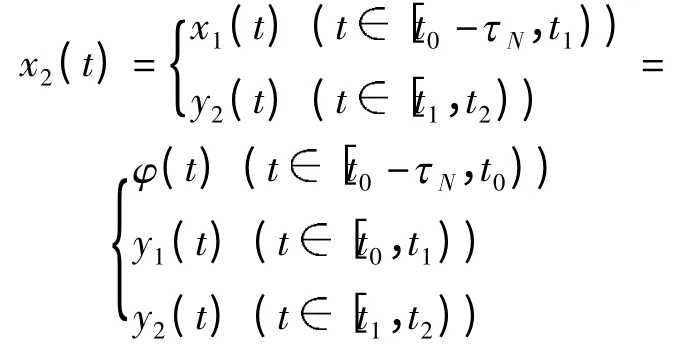
为问题(3)在区间［t0－τN，t2)上的一个解.

同理，对t=tk(kN)，考虑问题

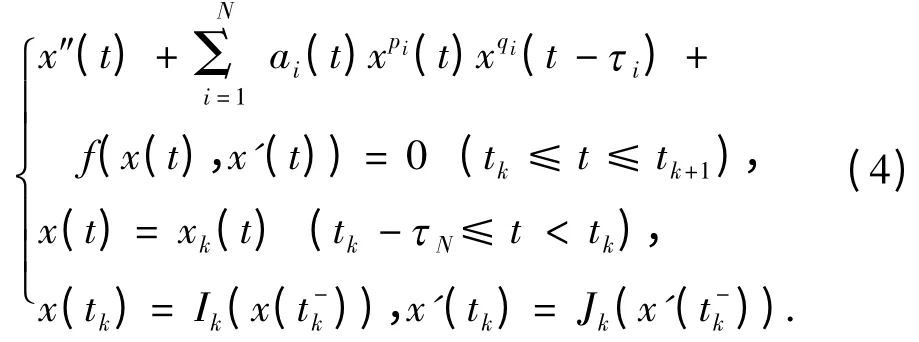
记Kk=φ∪{t1，t2，…，tk}，定义算子Nk(［tk－τN，tk+1］，R)→(［tk－τN，tk+1］，R)为

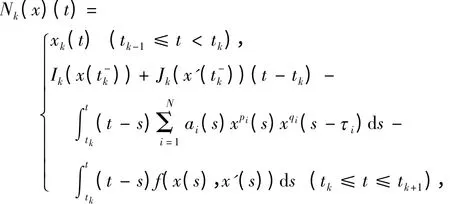
由性质(1)～(4)，Nk存在一个不动点，设为yk(t)，且有

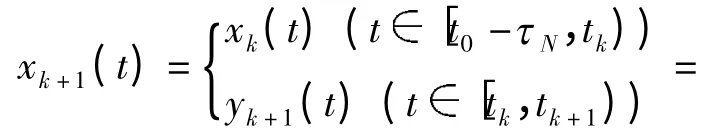
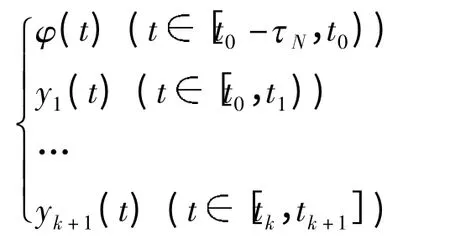
为方程(1)和条件(2)在区间［t0－τN，tk+1)上的一个解. 重复以上，可得

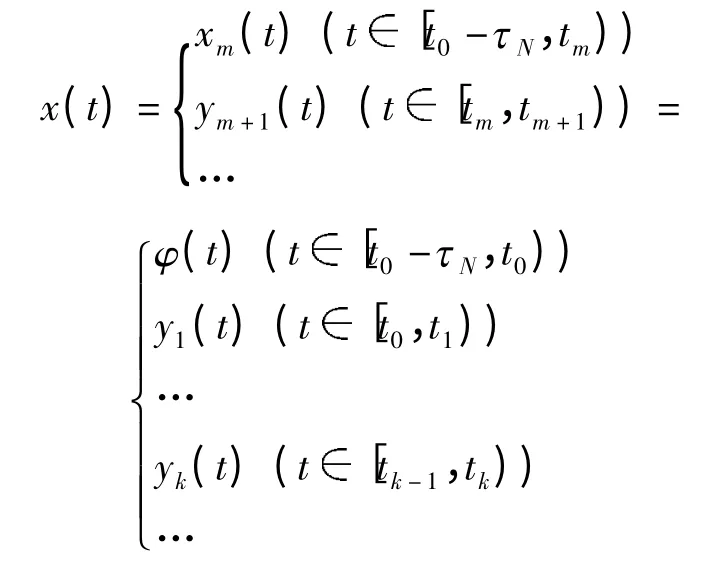
为方程(1)和条件(2)在区间［t0－τN，+∞)上的一个解. 证毕.

注1 若设置脉冲条件:τN≤tk+1－tk≤l，则条件(H2)可用ANl2≤1 替换，定理结论仍成立.

引理2［9］(Young 不等式)设a，b≥0，0 ＜λ ＜1，则aλb1－λ≤λ a+(1－λ)b 成立.

定理2 设条件(H1)～(H3)均成立，f(x，y)y≥0 (x，yR). 若有

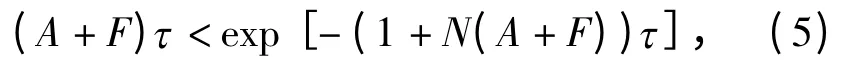
证明 设式(5)成立，则存在α ＞0 和l≥τ 使得

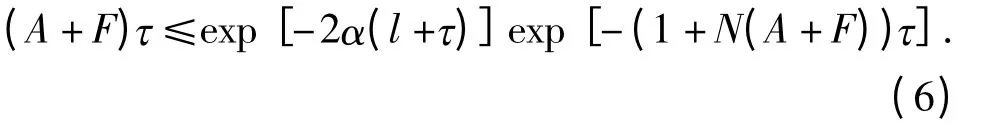
对任给单调递增数列{tk}kN→+∞，τN≤tk－tk－1≤l，令:Ⅰk(u)= Jk(u)= dku (kN)，其中dk=exp［－(1 +(A +F)N)(tk+1－tk)］. 显然dk≥0，pk≥(A+F)τ. 取

(1)0 ＜pi≤1. 令t［t0，t1)，定义Liapunov 函数V(t)为

显然V(t)≥x2(t)+x'2(t)，且V(t)满足如下结论:

(i)V(t)≤［1 +(A +F)τ］［‖xt‖2+x'2(t)］，其中

证明如下:

由

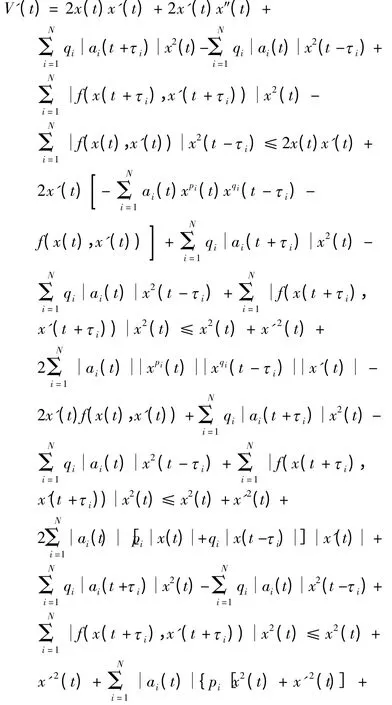
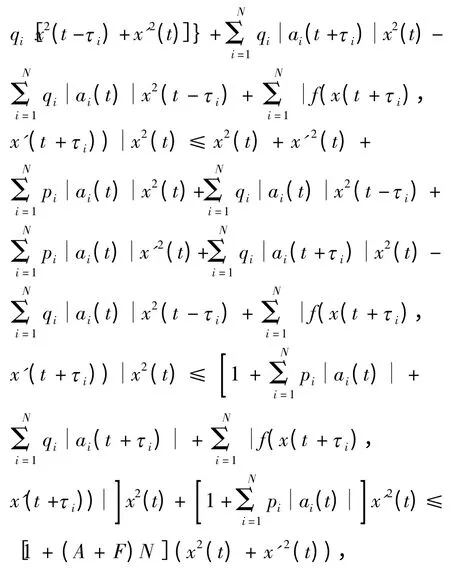
及(i)可知

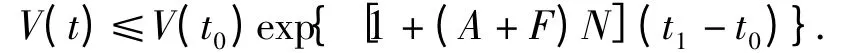
则有

则

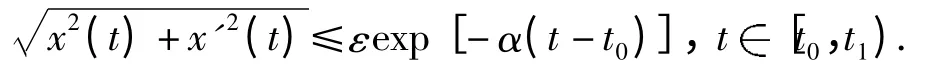
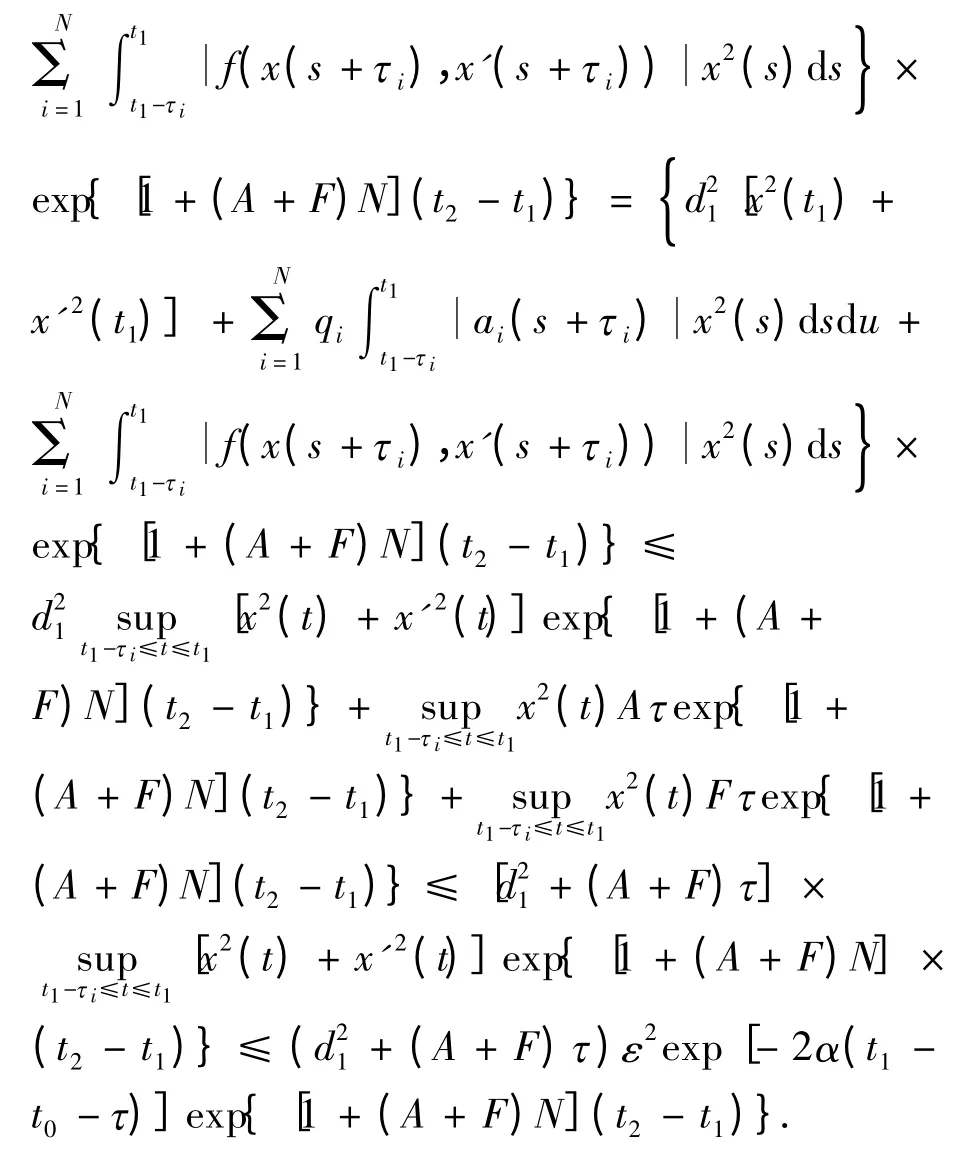
根据d1、p1的定义及V(t)性质，有

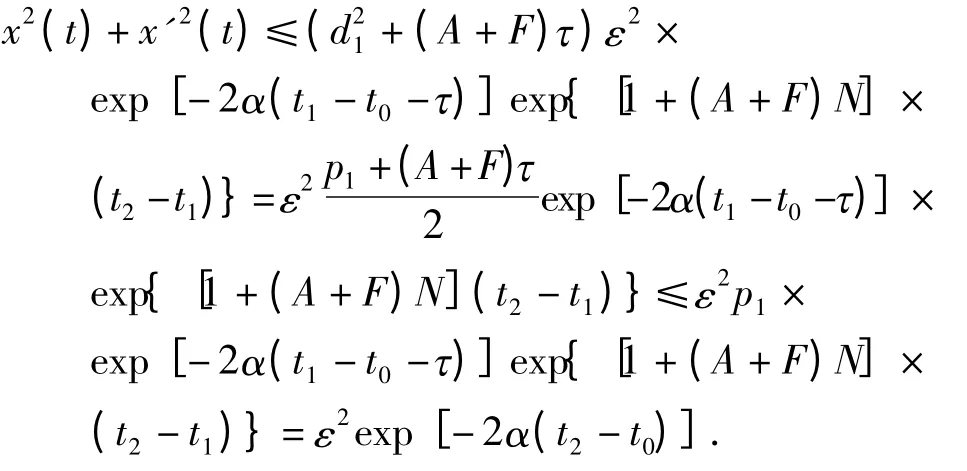
则

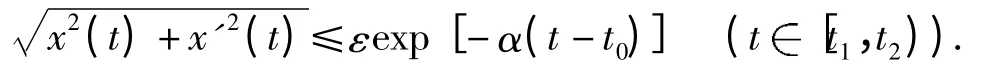
同理可证当k=1，2，…，

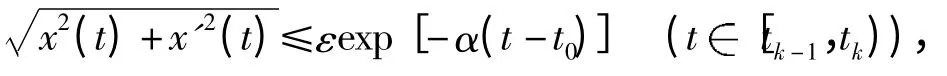
即

(2)pi=0. 定义Lyapunov 函数V(t)为

类似情形(1)的证明过程可证之. 证毕.

下面给出2个例子:

例1 考察方程

初始条件为:x(t)=φ(t)，－2≤t≤0，x'(0)=y0.

易知方程(7)的特征方程为

用Matlab 软件知方程(8)有一带正实部根，因而知方程(7)的零解是不稳定的.

令A=0.000 21，l =τ =τ1+τ2=3 和α =1/12，则

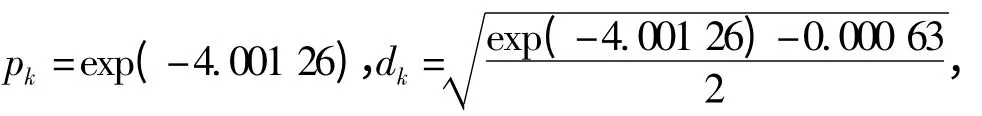
由定理2 知方程(7)的解在［0，+∞)可指数稳定.

例2 考察方程

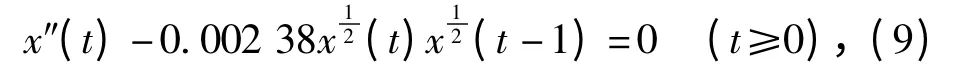
初始条件为:x(t)=φ(t)，－1≤t≤0，x'(0)=y0.

令A=0.002 38，l=τ =1，α=1/4，则

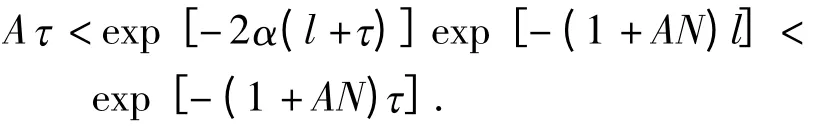
取例1 中脉冲条件，pk= exp(－2.002 38)，dk=则定理2 结论对式(9)仍成立.

［1］ANOKHIN A，BEREZANSK L，BRAVERMAN E. Exponential stability of linear delay impulsive differential equations［J］. Math Anal Appl，1995，195:923－941.

［2］BENCHOHRA M，HENDERSON J，NTOUYAS S K，et al. Higher order impulsive functional differential equations with variable times［J］. Dynam Syst Appl，2003，12:38－392.

［3］FENG Weizhen，CHEN Yongshao. The weak exponential asymptotic stability of impulsive differential system［J］.Appl Math Chinese Univ，2002，1:1－6.

［4］LI Xiang，WENG Peixuan. Impulsive stabilization of two kinds of second-order linear delay differential equations［J］. Math Anal Appl，2004，291:270－281.

［5］LIU X. Stability results for impulsive differential systems with applications to population growth models［J］. Dynam Stability Systems，1995，10:5－12.

［6］GIMENES L P，FEDERSON M. Existence and impulsive stability for second order retarded differential equations［J］. Appl Math Comput，2006，177:44－62.

［7］LAKSHMIKANTHAM V，BAINOV D D，SIMEONOV P S. Theory of impulsive differential equations［M］. Singapore:World Scientific，1989.

［8］SMART D R. Fixed point theorems［M］. Cambridge:Cambridge University Press，1980.

［9］匡继昌. 常用不等式［M］. 3 版.济南:山东科学技术出版社，2003.