MRCI+Q理论研究SiSe分子X1Σ+和A1Π电子态的光谱常数和分子常数*

邢伟 刘慧 施德恒 孙金锋 朱遵略

1)(信阳师范学院物理电子工程学院,信阳 464000)

2)(河南师范大学物理与信息工程学院,新乡 453007)

(2012年7月30日收到;2012年9月25日收到修改稿)

1 引言

Si和Se是重要的半导体材料和光敏材料,因此,由Si元素和Se元素组成的SiSe有望成为新型的半导体材料和光敏材料.众所周知,分子和光谱特性的详细知识,可以为改进和发展半导体材料和光敏材料制备工艺中的光谱检测技术提供理论依据.为了获得SiSe分子精确的分子和光谱性质,在过去的几十年里,研究人员对此做了一些实验和理论研究[1−12].

1939年,Barrow[1]首次通过Al和Se在石英管里高温放电研究了2914—3671˚A范围内D1Π—X1Σ+紫外发射谱带,并对其进行振动分析得到X1Σ+和D1Π态部分光谱常数.1946年,Barrow和Vago[2,3]观察了2450—2770范围内SiSe分子新的紫外吸收光谱(E1Σ+—X1Σ+),对其进行振动分析并提高了X1Σ+,D1Π和E1Σ+态部分光谱常数的精度.1965年,Hoeft[4]研究了SiSe分子基态最低的三个振动能级的微波吸收光谱,并确定了SiSe分子几种同位素的非常精确的转动常数.1977年,Bosser等[5]对SiSe分子 D1Π—X1Σ+和a3Π—X1Σ+跃迁进行了高分辨率的转动分析,并把D1Π态重新命名为后来所用的A1Π态,而且得到了 X1Σ+态的光谱常数(ωe和ωexe)以及 A1Π态的光谱常数(Te,Re,ωe和ωexe).1979年,Huber和Herzberg[6]把文献[1,2,4]中SiSe(X1Σ+和A1Π)分子的光谱结果收集在他们的专著中.1988年,Lakshminarayana和 Shetty[7]观察了 4000—6000范围内E1Σ+—X1Σ+跃迁的很多波带,并获得了28Si80Se同位素分子X1Σ+电子态和E1Σ+电子态精确的转动常数.1993年,他们[8]又对28Si80Se同位素分子A1Π—X1Σ+系统进行了高分辨率的研究,并获得了A1Π态转动常数(Bυ和Dυ)和振动常数(Te,ωe和ωexe).最近,Giuliano等[9]利用脉冲喷气谐振器的傅里叶变换微波谱仪测量了SiSe的8个同位素分子X1Σ+电子态的纯转动光谱,对其进行Dunham分析,得到了包含28Si80Se(X1Σ+)分子的光谱常数 (Re,ωe,ωexe,Be和αe).综合已有的实验数据可以看出,这些实验结果主要集中于该分子X1Σ+和A1Π态光谱常数的研究;仅文献[8]报道了A1Π态的部分低振动态的惯性转动常数Bυ和离心畸变常数Dυ.

理论上,SiSe分子最早的从头计算结果是Andrews等[10]1996年报道的.Andrews等利用B3LYP密度泛函理论和6-311G∗基组计算了SiSe(X1Σ+)分子的个别光谱常数(Re,ωe).2003年,Chattopadhyaya等[11]采用多参考双重激发组态相互作用方法(MRDCI)和相对论的有效核心势(RECP)在0.105—0.529 nm的核间距范围内计算了该分子X1Σ+和A1Π态的势能曲线,拟合得到这两个态的部分光谱常数(Re,De,ωe和Te).2009年,Jiao等[12]采用密度泛函(B3LYP)方法及6-311+G(d)基组计算了SiSe分子基态的势能曲线,并利用最小二乘法将其拟合成M-S势能函数,从而得到SiSe分子基态的光谱常数.但是,这些计算大多集中于研究基态的光谱特性.仅文献[11]研究了A1Π态的光谱特性.

对势能曲线进行标量相对论修正和外推能量至完全基组极限对于精确的预测光谱常数和分子常数有重要的影响.总结文献[10—12]中的理论光谱结果,发现仅文献[11]的势能曲线的计算中采用了高精度的MRDCI方法并考虑了相对论效应的影响.但是他们的计算中既没有修正MRDCI存在的“大小一致性”误差,也没有把这两个电子态的势能曲线外推至完全基组极限,因此拟合出的主要光谱常数(De和Te)的精度较差.另外,没有一篇理论文献涉及该分子X1Σ+和A1Π态的分子常数的研究.并且,X1Σ+态前30个振动态的Bυ和Dυ以及A1Π态的较高振动态的Bυ和Dυ既没有实验测量也没有理论研究.因此,理论上必须深入地研究SiSe分子X1Σ+和A1Π态的光谱特性和分子特性.

本文研究安排如下:首先采用Davidson修正的内收缩多参考组态相互作用方法(MRCI+Q)[13,14]及较大的相关一致基aug-cc-pV5Z(AV5Z)和augcc-pVQZ(AVQZ)[15,16]计算 SiSe(X1Σ+和 A1Π)分子的势能曲线;接着借助于两点总能量外推公式得到完全基组极限时的势能曲线;然后对完全基组极限时的势能曲线进行标量相对论修正,以得到X1Σ+和A1Π态较精确的势能曲线;最后,利用MRCI+Q/Q5+DK理论水平的势能曲线获得了这两个态的光谱常数 (Te,De,Re,ωe,ωexe,ωeye,Be和αe)和J=0时前30个振动态的Bυ和Dυ等分子常数,并把本文计算的光谱常数和分子常数与以前文献报道的结果进行比较.

2 计算方法

为得到SiSe(X1Σ+和A1Π)分子势能曲线和精确的De,本文在0.105—1.095 nm的核间距范围内进行了单点能计算.在每一单点能计算中,都首先利用Hartree-Fock方法得到体系的初始猜测轨道,接着使用完全活性空间自洽场(CASSCF)方法对体系的分子轨道和能量进行优化,然后利用CASSCF优化的波函作为参考波函,进行MRCI计算,最后使用Davidson修正MRCI结果带来的“大小一致性”误差.为保证势能曲线的计算精度,Si原子和Se原子都采用较大的相关一致基aug-cc-pV X Z(X=Q,5).计算步长取0.02 nm.在平衡位置附近,为获得势能曲线的细节信息,步长取0.002 nm.在0.105—1.095 nm的核间距范围内,计算得到的这两个态的势能曲线是完全收敛的.这意味着在1.095 nm处Si原子和Se原子完全分离,从而可以得到SiSe(X1Σ+和A1Π)分子的De.本文势能曲线的计算是在MOLPRO 2008.1程序包[17]中进行的.

MOLPRO在处理酉矩阵对角化过程中使用Abelian点群.对于具有简并对称性的分子,则必须使用Abelian子群.也就是说,本文的SiSe分子具有C∞v对称性,计算中必须由C2v对称性替代.换句话说,在CASSCF及其随后的MRCI+Q计算中必须考虑这4种类型的轨道:a1/b1/b2/a2.具体地说,在计算SiSe(X1Σ+和A1Π)分子的势能曲线时,选用9个分子轨道(5,2,2,0)作为活性空间,这些轨道对应于Si原子的3s3p4s和Se原子的4s4p壳层的所有原子轨道.Si原子最外层的3s23p2和Se原子的4s24p4电子处于这个活性空间中,其余电子则放入19个闭壳层轨道(10a1,4b1,4b2和1a2)中.另外,Se原子3d壳层10个电子用于考虑核价相关效应,但不参与激发,剩余的内部电子被冻结.也就是说,共有20个电子参与电子相关效应的计算.当采用这28个分子轨道(15a1,6b1,6b2和1a2)计算SiSe(X1Σ+和A1Π)分子的绝热势能曲线时,在目前的核间距范围内所得的势能曲线既光滑、又收敛.

在高水平的从头计算中,必须消除基组截断误差.消除基组截断误差最有效的方法是外推能量到完全基组极限.本文利用M¨uller等[18]的两点总能量外推公式

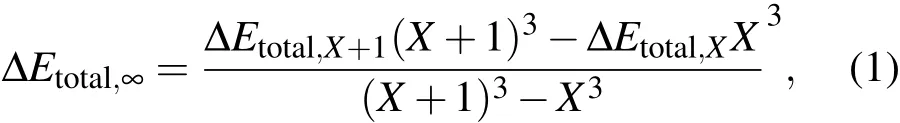
其中,∆Etotal,∞是外推至完全基组极限的总能量.∆Etotal,X和 ∆Etotal,X+1分别是由 aug-cc-pV X Z和aug-cc-pV(X+1)Z基组计算的总能量.本文使用AVQZ和AV5Z基组进行计算,并结合(1)式,得到完全基组极限时的势能曲线(记为MRCI+Q/Q5).

由于Se原子较重,其相对论效应影响显著,本文采用三级Douglas-Kroll-Hess哈密顿(DKH3)近似考虑标量相对论效应,因为在DKH3近似下得到的总能量最接近四分量完全相对论结果[19−21].更确切地说,利用cc-pV5Z-DK基组并使用DKH3近似得到的势能值减去仅在cc-pV5Z基组下的势能值,即得到势能的标量相对论修正值.将这一修正值加到MRCI+Q/Q5理论水平下的势能计算结果中,便得到经标量相对论效应修正的势能曲线(记为MRCI+Q/Q5+DK).

利用Molcas 7.4程序包中的VIBROT模块[22]拟合MRCI+Q/Q5+DK理论水平上的势能曲线,即可得到这两个电子态的光谱常数,其结果列于表1中.为便于比较,表1中也列出了实验结果[3,5−9]和其他理论计算结果[10−12].

3 结果与讨论

3.1 光谱常数

通过分析HF和CASSCF波函,发现SiSe分子 X1Σ+态的电子组态为 1σ22σ∗23σ21π44σ∗25σ22π∗46σ∗27σ23π48σ∗29σ21δ210σ∗24π∗411σ212σ∗25π413σ2.13σ—6π∗的激发形成激发电子态 A1Π.SiSe分子的X1Σ+和A1Π电子态的离解极限都是原子基态Si(3Pg)+Se(3Pg).图1为MRCI+Q/Q5+DK水平上计算得到的这两个态的势能曲线.

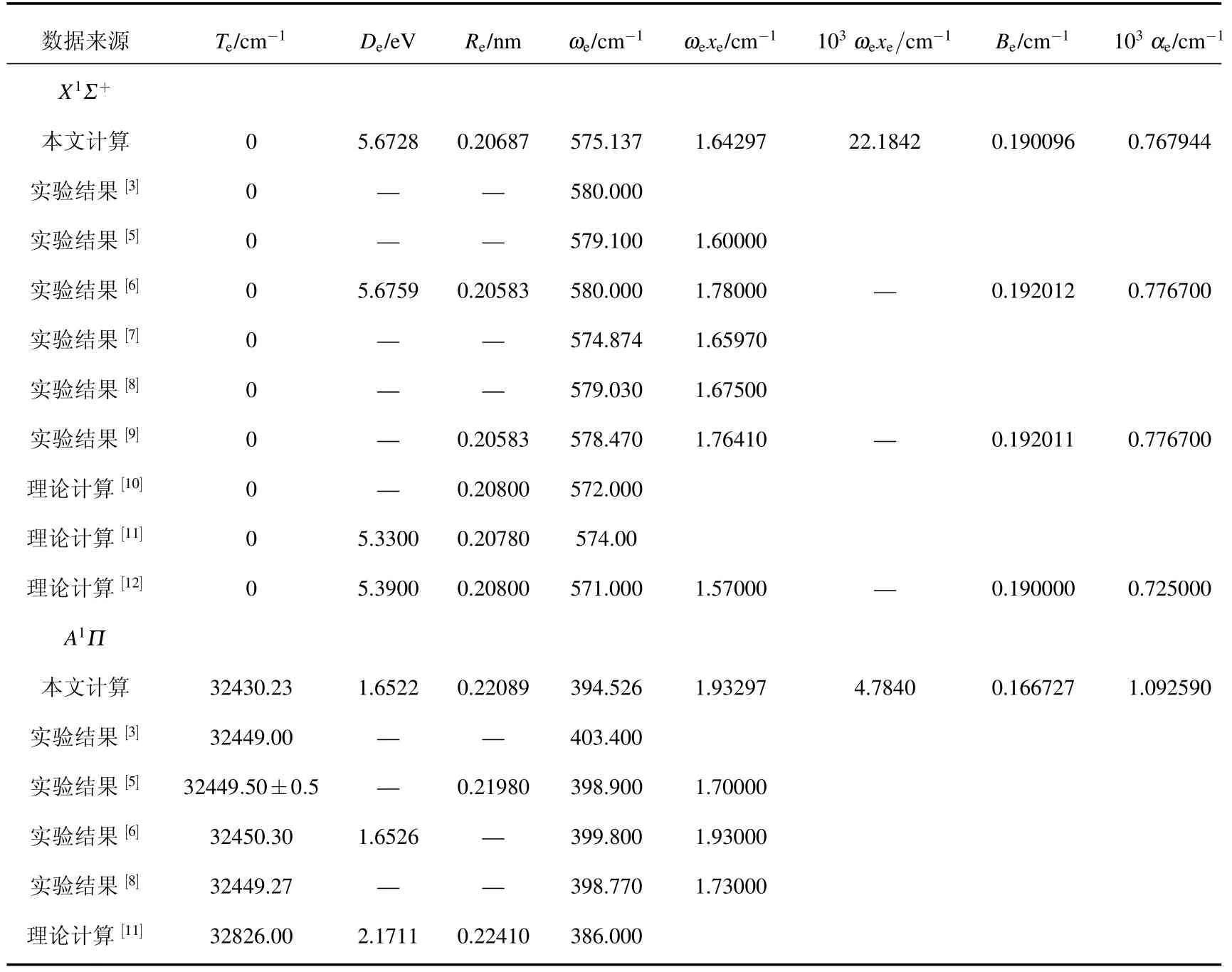
表1 MRCI+Q/Q5+DK理论水平上28 Si80Se(X1Σ+和A1Π)分子的光谱常数及与实验结果和其他理论结果的比较

图1 SiSe分子两个态的势能曲线 1,X1Σ+;2,A1Π

为了确定SiSe(X1Σ+和A1Π)分子的光谱结果,文献[10—12]对其进行了理论研究.正如表1中所示,总体上,本文的计算结果比理论值[10−12]更接近测量值[3,5−9].例如,对于基态,本文计算所得的De,Re,ωe,ωexe,Be和αe与实验值 [3,5,9]的最大偏离分别为0.0031 eV(0.055%),0.00104 nm(0.505%),4.863 cm−1(0.8384%),0.13703 cm−1(7.6983%),0.001916 cm−1(0.9979%) 和 8.756× 10−6cm−1(1.1273%). 对于 A1Π 态,本文计算所得的T e,D e,R e,ωe和 ωe x e与实验值 [3,5,6,8]的最

大偏离分别为20.07 cm−1(0.0618%),0.0004 eV(0.0242%), 0.00109 nm (0.496%), 8.874 cm−1(2.1998%),0.23297 cm−1(13.704%).由于没有实验和其他的理论文献报道X1Σ+和A1Π态的ωeye以及A1Π态的Be和αe值,因此,计算结果的准确度无法进行比较.

通过以上比较可以看出,X1Σ+和A1Π电子态的主要光谱常数(Te,De,Re,ωe)与实验结果[3,5−9]非常符合,说明MRCI+Q/Q5+DK下获得的X1Σ+和A1Π电子态的势能曲线是准确和可靠的.

3.2 分子常数

利用MRCI+Q/Q5+DK下计算得到的X1Σ+和A1Π电子态的势能曲线,借助于Molcas 7.4程序包中的VIBROT模块[22],利用Numerov’s方法通过求解核运动的振转Schr¨odinger方程,计算了J=0时该分子这两个电子态每一振动态的Bυ和Dυ等分子常数.由于篇幅限制,表2中仅分别列出J=0时这2个电子态的前30个振动态的Bυ和Dυ.

据我们所知,迄今为止,没有实验和理论文献报道X1Σ+电子态J=0时前30个振动态的Bυ或Dυ,仅Lakshminarayana和Shetty[8]1993年报道了A1Π电子态前5个振动能级对应的Bυ和Dυ.为了便于比较,我们把仅有的实验文献[8]中A1Π电子态的Bυ和Dυ值列入表2.不难发现本文计算的Bυ和Dυ值与实验值[8]非常符合.例如,当υ=0—4时,本文计算的Bυ与实验[8]的偏离仅为0.00143(0.856%),0.00138(0.828%),0.00129(0.777%),0.00110(0.672%)和 0.00087(0.535%).由于Dυ是高阶小量,本文的计算结果与实验[8]的差异并不大.这些比较结果说明表2给出的A1Π态的低振动态的Bυ和Dυ值是相当准确的.尽管对A1Π态较高的振动态的Bυ和Dυ来说,目前暂无实验结果或其他理论计算结果可供比较,由于本文方法已被证明十分可靠[23−30],并且表2列出的A1Π态的分子常数来自同一势能曲线和同一拟合方法,因此我们有理由相信,表2列出的A1Π态高振动态的Bυ和Dυ也是可靠的.

由上面的讨论可知,本文在MRCI+Q/Q5+DK下获得的A1Π电子态的分子常数与实验值非常一致.由于本文得到2个电子态分子常数所用的计算方法和拟合方法完全一样,因此,我们有理由相信表2列出的X1Σ+电子态Bυ和Dυ值是准确和可靠的.

3.3 残余误差分析

尽管MRCI+Q/Q5+DK上计算的结果与实验结果[3,5−9]符合得非常好,但仍旧存在残余误差.

MRCI+Q理论方法在计算中虽然修正了MRCI方法存在的“大小一致性”误差,但在计算中截断了四级以上激发级别参考波函的展开式,因此,未考虑MRCI+Q方法存在的四级以上的电子激发是本文残余误差的第一个主要来源.

此外,本文残余误差的第二个主要来源是未考虑核价相关效应,如果在势能曲线的计算中考虑了Si和Se的核电子,在一定意义上可以提高所得的光谱常数的精度.但是为了得到这两个态光滑的势能曲线,我们在计算中将1个额外的a1轨道放入了活化空间.额外的分子轨道将使核价相关修正消耗大量的内存时间,因此,在目前的研究中未考虑核价相关修正.若在计算中纳入核价相关修正或多或少可以提高光谱常数的质量.例如,核价相关修正可以使Re缩短,Te和ωe增大[27−30],从而使X1Σ+和A1Π电子态的光谱常数更接近实验值[3,5−6,8,9].

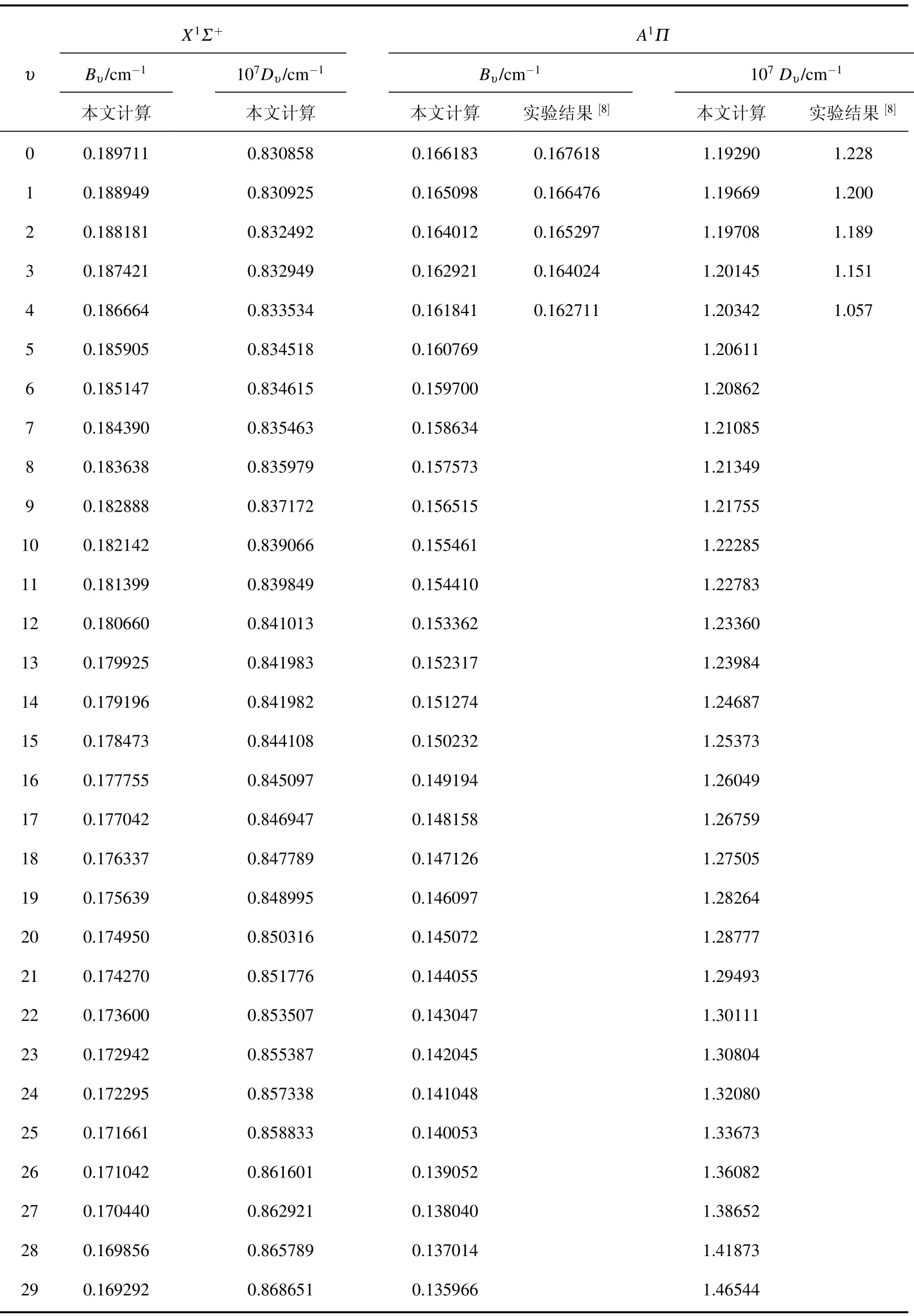
表2 MRCI+Q/Q5+DK理论水平得到的J=0时28Si80 Se分子X1Σ+和A1Π态的Bυ和Dυ值及与实验结果的比较

为了得到比较精确的结果,在本文的势能曲线计算中,采用DKH3近似进行标量相对论修正.由于在DKH3近似下得到的总能量最接近四分量完全相对论结果,因此,我们认为采用DKH3近似进行相对论修正来处理相对论效应的影响是足够的.也就是说,近似地处理相对论效应带来的残余误差可能非常小.

4 结论

本文利用MRCI+Q方法和相关一致基AV5Z和AVQZ,在0.105—1.095 nm的核间距范围内分别计算了SiSe分子X1Σ+和A1Π电子态的势能曲线.为提高势能曲线的计算精度,利用两点总能量外推公式,将这两个电子态的势能曲线外推至完全基组极限,并对其进行了标量相对论修正,相对论效应是在cc-pV5Z基组水平下使用三级Douglas-Kroll-Hess哈密顿算符计算的.利用MRCI+Q/Q5+DK理论水平的势能曲线获得了这两个态的光谱常数(Te,De,Re,ωe,ωexe,ωeye,Be和αe)和J=0时前30个振动态的Bυ和Dυ等分子常数,其值与已有的实验结果非常一致.本文得到的光谱常数和分子常数达到了很高精度,能为进一步的光谱实验和理论研究提供可靠参考.

[1]Barrow R F 1939 Proc.Phys.Sot.51 267

[2]Vago E E,Barrow R F 1946 Proc.Phys.Sot.58 538

[3]Vago E E,Barrow R F 1946 Nature 157 77

[4]Hoeft J 1965 Z.Naturforsch.A 20 1122

[5]Bosser G,Lebreton J,Marsigny L 1977 J.Chem.Phys.77 13

[6]Huber K P,Herzberg G 1979 Molecular Spectra and Molecular Structure(Vol.4)Constants of Diatomic Molecules(New York:Van Nostrand Reinhold)p608

[7]Lakshminarayana G,Shetty B J 1988 J.Mol.Spectrosc.130 155

[8]Lakshminarayana G,Shetty B J 1993 J.Mol.Spectrosc.161 575

[9]Giuliano B M,Bizzocchi L,Grabow J U 2008 J.Mol.Spectrosc.251 261

[10]Andrews L,Hassanzadeh P,Lanzisera D V,Brabson GD 1996 J.Phys.Chem.100 16667

[11]Chattopadhyaya S,Das K K 2003 Chem.Phys.Lett.382 249

[12]Jiao D S,Wang H Y 2009 J.Sichuan.Univ.(Nat.Sci.Ed.)46 999

[13]Langhoff S R,Davidson E R 1974 Int.J.Quantum Chem.8 61

[14]Richartz A,Buenker R J,Peyerimhoff S D 1978 Chem.Phys.28 305

[15]Woon D E,Dunning T H 1993 J.Chem.Phys.98 1358

[16]Dunning T H 1989 J.Chem.Phys.90 1007

[17]Werner H J,Knowles P J,Lindh R,Manby F R,Sch¨utz M,Celani P,Korona T,Mitrushenkov A,Rauhut G,Adler T B,Amos R D,Bernhardsson A,Berning A,Cooper D L,Deegan M J O,Dobbyn A J,Eckert F,Goll E,Hampel C,Hetzer G,Hrenar T,Knizia G,K¨oppl C,Liu Y,Lloyd A W,Mata R A,May A J,McNicholas S J,Meyer W,Mura M E,Nicklass A,Palmieri P,Pfl¨uger K,Pitzer R,Reiher M,Schumann U,Stoll H,Stone A J,Tarroni R,Thorsteinsson T,Wang M,Wolf A 2008 MOLPRO,Version 2008.1,a package of ab initio programs,http://www.molpro.net

[18]M¨uller T 2006 NIC Series 31 19

[19]Reiher M,Wolf A 2004 J.Chem.Phys.121 2037

[20]Wolf A,Reiher M,Hess B A 2002 J.Chem.Phys.117 9215

[21]Hirata S,Yanai T,Jong W A,Nakajima T,Hirao K 2004 J.Chem.Phys.120 3297

[22]Krogh JW,Lindh R,Malmqvist P˚A,Roos B O,Veryazov V,Widmark P O 2009 User Manual(Molcas Version 7.4)(Lund:Lund University)

[23]Shi D H,Xing W,Zhang X N,Sun JF,Zhu Z L,Liu Y F 2011 Comput.Theor.Chem.969 17

[24]Shi D H,Xing W,Sun J F,Zhu Z L,Liu Y F 2011 Comput.Theor.Chem.966 44

[25]Wang JM,Feng H Q,Sun JF,Shi D H 2012 Chin.Phys.B 21 023102

[26]Wang J M,Zhang L,Shi D H,Zhu Z L,Sun J F 2012 Acta Phys.Sin.61 153105(in Chinese)[王杰敏,张蕾,施德恒,朱遵略,孙金锋2012物理学报61 153105]

[27]Shi D H,Niu X H,Sun J F,Zhu Z L 2012 Acta Phys.Sin.61 093105(in Chinese)[施德恒,牛相宏,孙金锋,朱遵略2012物理学报61 093105]

[28]Xing W,Shi D H,Sun J F,Zhu Z L 2012 Int.J.Mol.Sci.13 8189

[29]Wang JM,Sun JF,Shi D H,Zhu Z L,Li WT 2012 Acta Phys.Sin.61 063104(in Chinese)[王杰敏,孙金锋,施德恒,朱遵略,李文涛2012物理学报61 063104]

[30]Liu H,Xing W,Shi D H,Sun J F,Zhu Z L 2012 Acta Phys.Sin.61 203101(in Chinese)[刘慧,邢伟,施德恒,孙金锋,朱遵略2012物理学报 61 203101]