具有随机节点结构的复杂网络同步研究*

刘金良

(南京财经大学应用数学学院,南京 210046)

(2012年8月18日收到;2012年9月20日收到修改稿)

1 引言

由于许多实际系统,如internet、电力系统、智能交通网络等都可以通过复杂网络模型进行描述,因此,近年来,复杂网络成为研究热点问题,受到物理、通信、计算机以及生命科学等领域学者的广泛关注[1−4].其中,复杂网络的同步问题更是备受关注.所谓复杂网络的同步是指性质相同或相近的两个或多个复杂网络,通过系统间的相互作用,使得在不同初始条件下的各种演化的复杂网络的状态逐渐接近,最后达到全同的状态.有关复杂网络的同步问题已经有很多研究成果.文献[5]利用滑模控制法对规则网络的混沌同步问题进行了研究,针对一个混沌系统进行控制或驱使一个混沌系统同步于另一个混沌态的滑模控制法推广到由多个混沌系统构成的复杂网络的同步研究中,同时设计了网络滑模面以及控制输入,并依据稳定性理论分析了它们的有效性.基于网络拆分思想并运用Lyapunov稳定性理论,文献[6]研究了一类具有非线性耦合的多重边赋权复杂网络,给出了该类复杂网络的同步准则.文献[7]对一类具有不相同节点和非线性扰动的复杂网络的同步问题进行了研究,作者通过使用自适应控制和脉冲控制的方法给出了具有更小保守性的复杂网络的同步判据.

与此同时,在实际的动态系统中,很多复杂网络系统的同步受到时滞的影响,如通讯网络总信号的传播通常是有时滞的,病毒在传播中也是存在一定的时滞的.而时滞可能导致复杂网络的系统性能下降,甚至震荡或不稳定,因此,为了更好地模拟实际网络,在复杂网络的建模过程中,应该充分考虑到时滞所到来的影响.文献[8,9]通过使用Lyapunov稳定性理论对一类具有耦合时滞的线性复杂网络系统进行了研究,给出了具有更小保守型的同步判据.文献[10]对一类具有耦合时滞的连续和离散的复杂网络动态系统的同步问题进行了研究,然后通过对时滞进行划分的思想,借助分段分析的方法得到了时滞依赖的复杂网络同步的充分性判据,由于该方法利用了更多的时滞信息,因此得到的结论具有更小的保守性.文献[11]对一类具有随机非线性和概率时滞的复杂网络研究了其族同步问题,然后基于随机分析的理论得到了复杂网络时滞概率分布依赖的族同步判据.

考虑复杂网络系统的复杂性,其动态系统的节点非线性是很难确定的,因此考虑其节点的随机变化就变得很有意义.已经有不少文献对节点互异的复杂网络进行了研究.文献[12]对星形网络和小世界网络进行了研究,结果表明随着耦合强度的增大,网络中相邻结点的两个系统之间存在相同步现象,而且相同步行为与定义的量化指标之间存在较准确的对应关系.文献[13]对节点结构互异的离散型时空混沌系统构成复杂网络的反同步问题进行了研究,通过构造合适的Lyapunov函数,确定了复杂网络中连接节点之间的耦合函数的结构以及控制增益的取值范围,进而发现整个网络存在稳定的混沌反同步现象.

基于上述讨论,本文研究了具有随机节点分布的复杂网络的同步问题,通过引入一个服从Bernulli分布的随机变量来表示节点的随机变化.通过使用Lyapunov稳定性理论和随机系统理论给出了该类复杂网络同步稳定的充分性判据,其中,这些判据是以便于计算机matlab求解的线性矩阵不等式的形式给出.需要指出的是,该充分性判据不仅与复杂网络的状态时延有关,还与节点结构的概率分布有关.

2 网络模型与预备条件

考虑由N个节点构成的连续复杂动态网络,每个节点是n维子系统,其模型为

其中 xi(t)=(xi1(t),xi2(t),···,xin(t))T∈ Rn为第 i个节点的状态变量;A,B是已知矩阵;f1(·),f2(·)∈Rn是连续可微的向量函数;Γl∈Rn×n(l=1,2)是已知的常数正定对角矩阵,表示内部耦合矩阵;G=(gij)∈RN×N是耦合配置矩阵,表示网络拓扑结构和节点间的耦合强度,其元素gij定义为:若在节点i和节点 j(i̸=j)间有连接,则gij=gji＞0,否则gij=gji=0(i̸=j).矩阵G的对角元素定义[11]为

τ(t)为时变时滞,满足τ1≤τ(t)≤τ2,其中 0≤τ1≤τ2,这里时滞下界τ1可以为0;δ(t)服从Bernulli分布,定义如下:

假设δ(t)满足

则

注1 与传统的复杂网络[3−5]不同的是,这里用服从Bernulli分布的随机变量δ(t)来表示复杂网络孤立节点动力学行为的随机变化.由δ(t)的定义可知,在复杂动态网络系统(1)中,非线性函数f1(·)与 f2(·)按照 δ(t)进行随机切换.

注2 系统模型(1)是具有一定代表性的复杂网络模型,首先该模型考虑了复杂网络节点动力学行为的随机变化,其次模型考虑了复杂网络节点的时滞,而且模型中既包含非时滞耦合项也包含时滞耦合项.

假设1 对任何u,v∈Rn,非线性函数 f1(·)与f2(·)满足以下扇形区域条件:

注3 由假设1可知

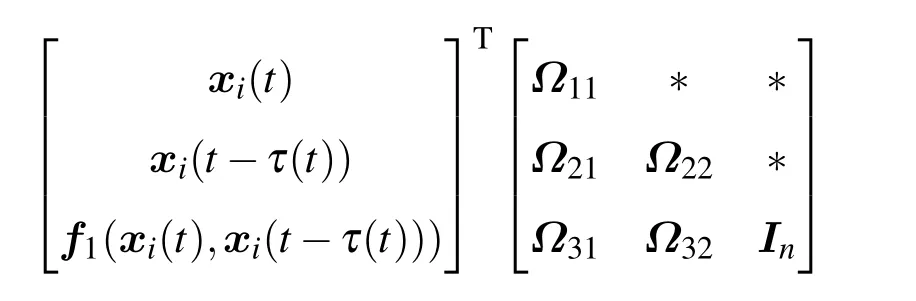
其中

∗表示对称矩阵所对应的对称元素(下同).

使用矩阵的Kronecker积,系统(1)可以重写为紧凑形式:

其中

给出本文主要结论之前,首先给出如下引理.

引理1[14]对给定的τ1≤τ(t)≤τ2,x(t)∈Rn,以及任意的正定矩阵R∈Rn×n,有

引理2[15]假定0≤τm≤τ(t)≤τM,1,2以及Ω是已知的维数匹配矩阵,则

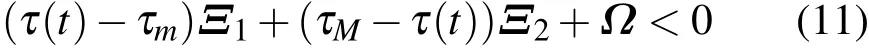
成立,当且仅当下面式子成立

3 主要结论

本节给出复杂网络(9)式同步的稳定性准则.定义

则复杂网络系统(9)式可以重写为

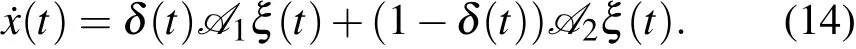
定理1 对于给定的时滞信息0≤τ1＜τ2和节点概率分布信息δ0∈[0,1],系统(1)同步渐近稳定,若存在正定矩阵P＞0,Q1＞0,Q2＞0,R1＞0,R2＞ 0,合适维数的矩阵 Ni,Mi(i=1,2,···,6),以及适当维数的对角矩阵Λ1和Λ2,使得下面的线性矩阵不等式对s=1,2成立:

其中

证明 构造如下形式的Lyapunov泛函:

其中V1(xt)=xT(t)P x(t),

则V(xt)沿系统(14)式求如下算子运算:

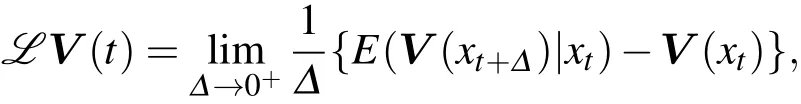
并对其取数学期望得:

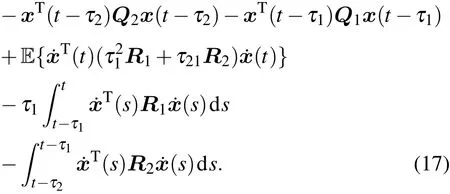
由引理1可知

而

由假设1和注3,存在对角阵Λ1和Λ2使得下式成立

应用自由权矩阵,有

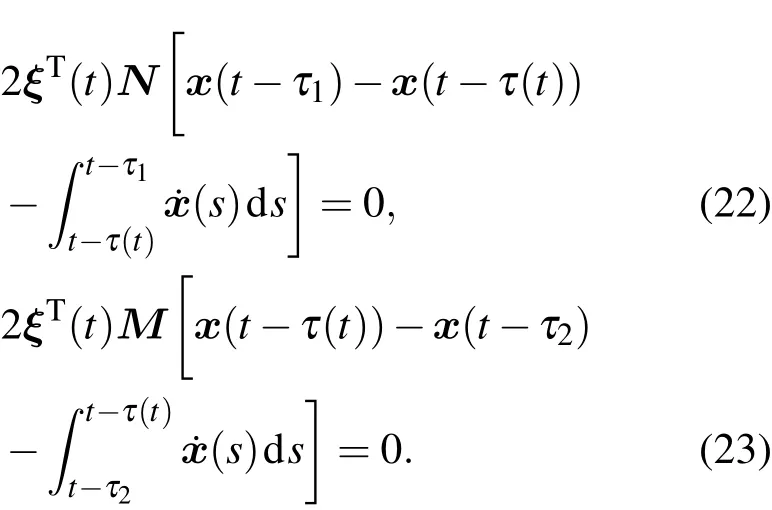
注意到存在矩阵R2,使得

将(22)和(23)式代入(17)式的右边,结合(18)—(25)式,可得

由(15)式可知,当s=1,2,利用Schur补引理,可得

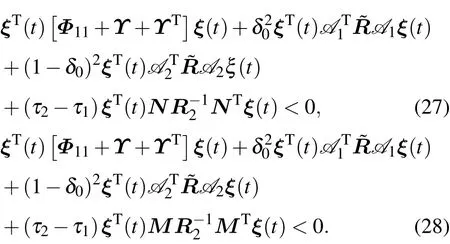
再由引理2,可得

利用Lyapunov稳定性理论,系统(14)式同步渐近稳定,于是复杂网络系统(1)的状态是同步渐近稳定的.

注4 由定理1可以看出,复杂网络系统(1)的同步渐近稳定不仅依赖于状态时延τ1,τ2,还依赖于节点结构的概率分布.

下面给出上面结果的一个特例,其证明类似定理1的证明.

当δ(t)=1,也即不考虑复杂网络系统(1)的随机节点结构的变化,此时系统(1)退化成

利用Kronecker积,系统(30)式可以重写为下面紧凑形式:

定义

则复杂网络系统(31)式可以重写为

类似于定理1,构造如下Lyapunov泛函

使用自由权矩阵N和M:

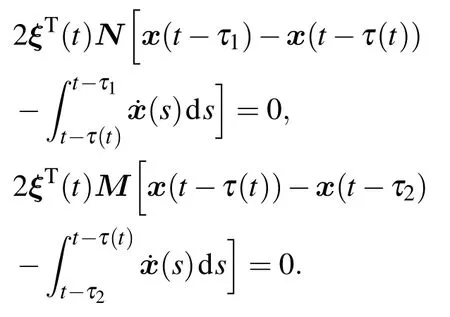
可以得到如下复杂网络(30)式同步的稳定性准则.

定理2 对于给定的时滞信息0≤τ1＜τ2,系统(30)同步渐近稳定,若存在正定矩阵P＞0,Q1＞0,Q2＞0,R1＞0,R2＞0,合适维数的矩阵Ni,Mi(i=1,2,···,5) 以及适当维数的对角矩阵Λ,使得下面的线性矩阵不等式对s=1,2成立:

其中

4 数值仿真

考虑如下具有5个节点的复杂网络系统,每个节点的动力学行为通过如下系统来描述:

其中

假设外部耦合矩阵与内部耦合矩阵可以分别通过如下形式给出:

当节点的概率分布δ0=0.7,令时滞下界τ1=0.1,通过定理1,通过使用matlab的LMI工具箱求解(15)式可得,时滞上界τ2=1.3,并且对不同的节点概率分布δ0,当τ1=0.1时,可以分别得到对应的时滞上界τ2(见表1).

选择如下初始条件:

当 τ1=0.1,τ2=1.2,δ0=0.6,可得图 1 和图 2 仿真曲线.其中,图1给出了时滞τ(t)的变化规律,图2给出了复杂网络系统(9)式的状态相应曲线,其中xj(i=1,2,···,5;j=1,2)表示第 i个节点的第j个状态,由该曲线可以看出该复杂网络可以很快达到同步.

图1 当τ1=0.1,τ2=1.2,δ0=0.6时,时滞τ(t)的变化曲线

表1 对于不同的δ0(τ1=0.1),系统所允许的最大时滞τ2

图2 当τ1=0.1,τ2=1.2,δ0=0.6时,复杂网络系统状态曲线

上面的算例里面,我们仅选择N=5,随着节点的增多,上面结论也能很好地使得系统达到同步.如其他条件不变,当N=10,外部耦合矩阵

当初始状态

复杂网络系统(9)式的状态相应曲线如图3所示.

图3 当τ1=0.1,τ2=1.2,δ0=0.6时,复杂网络系统状态曲线

5 结论

本文对一类具有随机节点分布的复杂网络的同步问题进行了研究.借助Lyapunov稳定性理论和随机系统理论给出了该类复杂网络同步稳定的充分性判据.其中,这些判据是以便于计算机matlab求解的线性矩阵不等式的形式给出.仿真算例表明了本文方法的有效性.

[1]Strogatz S H 2001 Nature 410 268

[2]Albert R,Barabasi A L 2002 Rev.Mod.Phys.74 47

[3]Wang J A 2012 Acta Phys.Sin.61 020509(in Chinese)[王健安2012物理学报61 020509]

[4]L¨u L,Liu S,Zhang X,Zhu J B,Shen N,Shang J Y 2012 Acta Phys.Sin.61 090504(in Chinese)[吕翎,柳爽,张新,朱佳博,沈娜,商锦玉2012物理学报61 090504]

[5]L¨u L,Li Y S,Wei L L,Yu M,Zhang M 2012 Acta Phys.Sin.61 120504(in Chinese)[吕翎,李雨珊,韦琳玲,于淼,张檬2012物理学报61 120504]

[6]Bian Q X,Yao H X 2010 Acta Phys.Sin.59 3027(in Chinese)[卞秋香,姚洪兴2010物理学报59 3027]

[7]Yang X,Cao J,Lu J 2012 IEEE Trans.Circuits Sys.I 59 371

[8]Zhang Q,Zhao J 2012 Chin.Phys.21 040502

[9]Gao H,Lam J,Chen T 2006 Phys.Lett.A 360 263

[10]Yue D,Li H 2010 Neurocomputing 73 838

[11]Li H 2011 J.Phys.A:Math.Theor.44 105101

[12]Lu J,Zhang R,Xu Z Y 2010 Acta Phys.Sin.59 5949(in Chinese)[卢静,张荣,徐振源2010物理学报59 5949]

[13]L¨u L,Liu S,Zhang X,Zhu J B,Shen N,Shang J Y 2012 Acta Phys.Sin.61 090504(in Chinese)[吕翎,柳爽,张新,朱佳博,沈娜,商锦玉2012物理学报61 090504]

[14]Gu K,Kharitonov V,Chen J 2003 Stability of Time-Delay Systems(Berlin:Springer)p315

[15]Yue D,Tian E,Zhang Y 2009 Int.J.Robust Nonlin.19 1493