旋转环形浅液池内双组分溶液耦合热-溶质毛细对流渐近解*
龚振兴 李友荣 彭岚 吴双应 石万元
(重庆大学动力工程学院,低品位能源利用技术及系统教育部重点实验室,重庆 400044)
(2012年5月31日收到;2012年9月14日收到修改稿)
1 引言
液体的表面张力会随温度和浓度的不同而发生变化,在双组分混合溶液中,当自由表面同时存在温度和浓度梯度时,将会产生表面张力梯度,从而驱动流体流动,这种流动通常被称为耦合热-溶质毛细对流.耦合的毛细对流过程广泛存在于晶体生长、合金凝固、混合工质的相变传热等过程中[1−3].
Bergman[4]最先对水平温度梯度和浓度梯度作用下矩形池内耦合热-溶质毛细对流进行了数值模拟,主要讨论了热和溶质毛细力大小相等、方向相反的特殊情况,研究表明,当热Marangoni数超过临界值时,流体将由静止状态转变为流动状态.Bergeon等[5]采用二维数值模拟和稳定性分析方法研究了垂直温度梯度作用下矩形池内双组分溶液Marangoni对流现象,分析了Soret效应对流动的影响,结果表明,当Soret效应足够大时,溶质梯度驱动的Marangoni流动起主导作用,同时,讨论了流体流动的分岔现象.Arafune等[6,7]对Bergman的研究进行了拓展和完善,发现了多种流型的存在,并对流动出现分岔的物理机制进行了解释.Chen和Chan[8]采用稳定性分析、数值模拟和实验观测相结合的方法研究了腔体内表面张力和浮力驱动的流动稳定性,得到了流动失稳的临界条件.Cr¨oll等[2]借助实验研究了Czochralski法晶体生长过程中锗-硅熔体内溶质毛细对流现象,测定了不同重力水平下熔体的流动速度.Li等[9]和Chen等[10]对水平温度梯度和浓度梯度作用下矩形池内Marangoni对流现象进行了稳定性分析和二维数值模拟,其主要针对热和溶质毛细力大小相等、方向相反的特殊情况,获得了流体的流型转变规律,并分析了物性参数和几何形状对传热和传质速率的影响.随后,Zhan等[11]在Li等[9]和Chen等[10]研究的基础上采用三维数值模拟方法对矩形池内Marangoni对流现象、流型的演变以及物性和几何参数对传热传质的影响进行了系统研究.此外,Li等[12]和Shi等[13]对旋转环形液池内的热毛细流动现象也进行了研究,Zheng等[14,15]和Zhang等[16]获得了Marangoni对流边界层近似解析解.然而,对于旋转环形池内水平温度和浓度梯度作用下耦合热-溶质毛细对流的研究鲜有报道.匹配渐近展开法是研究流体流动的一种常用的有效方法.Cormack和Leal[17],Merker和Leal[18],Leppinen[19]用这种方法求解了两侧边壁具有温度差的矩形和环形浅液池内流体自然对流过程;Li等[20−22]将这种方法进行了拓展,研究了环形单层及双层浅液池内热毛细对流和热毛细-浮力对流过程,获得了中心区域近似解.本文的目的是采用匹配渐近展开法研究旋转环形浅液池内耦合热-溶质毛细对流过程,同时分析旋转、Soret效应、浮力、溶质扩散系数和几何尺寸对流动的影响.
2 物理数学模型
假定环形浅液池内半径为ri,外半径为ro,深度为h,宽度为l,则ro=ri+l.液池底部为固壁,顶部为不变形的自由界面,底部和顶部均绝热,如图1所示.液池深宽比ε=h/l,对于浅液层,ε→0.记液池几何参量Γ=ri/l,δ=ri/h,则Γ=εδ.设液池按逆时针方向绕垂直中心轴旋转,转速为每分钟n转.内、外壁分别维持恒温TC和Th(Th>TC).初始时刻液池内溶质浓度分布均匀,比重较大组分的溶质质量分数为N0,质量浓度为S0.为简化起见,假定:1)流体为不可压缩的牛顿流体,除表面张力和浮力项中的密度外,所有的物性参数都为常数;2)温差∆T=Th−TC较小,液池转速较低,流动为轴对称二维稳态层流;3)在顶部自由表面考虑热和溶质毛细力作用,且表面张力是温度和浓度的线性函数;4)所有固壁无质量渗透,且满足无滑移条件;5)考虑Soret效应的影响,忽略Dufour效应.
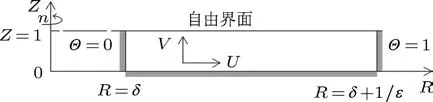
图1 浅液池的物理模型
分 别 将 εν/h, ρν2/h2, Th− TC, ∆S=−DTSSo(1−No)(Th−TC)/D(DTS=ST·D,ST为Soret系数)和h作为控制方程的无量纲参考速度、压力、温度、浓度和长度,并引入无量纲流函数ψ和涡量ω:

则无量纲化后的控制方程组为
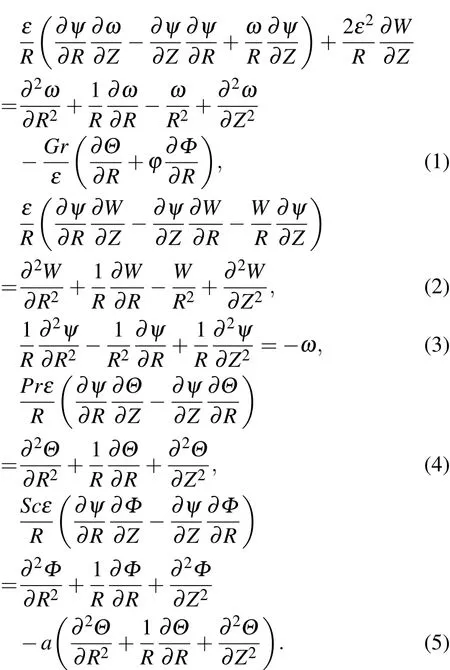
定义常数a,当考虑Soret效应时,a=1,反之a=0.相应的无量纲边界条件为

其中,R和Z分别为无量纲坐标;U,V和W分别为无量纲的径向、轴向和周向速度.上述各式中其他无量纲量定义如下:
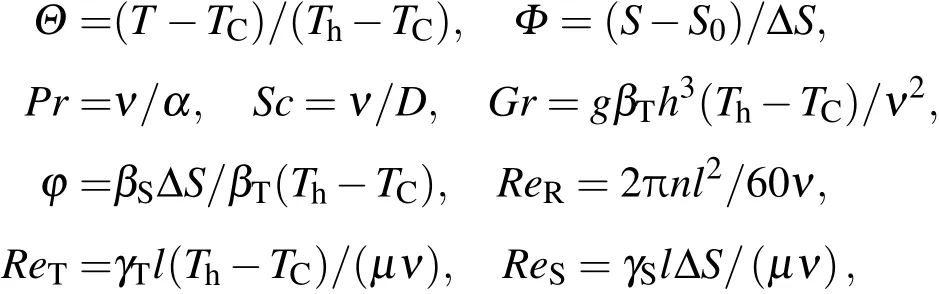
其中,Θ为无量纲温度,Φ为无量纲浓度,Pr为普朗特数,Sc为施密特数,Gr为格拉晓夫数,φ为浓度不均匀和温度不均匀引起的浮力比,ReR为旋转毛细雷诺数,ReT和ReS分别为热毛细雷诺数和溶质毛细雷诺数,ν,α和D分别为流体的运动黏度系数、热扩散率和质量扩散率;βT=−ρ∂ρ/∂T和 βS=−ρ∂ρ/∂S分别为温度和浓度体积膨胀系数;γT= −∂σ/∂T 和 γS= −∂σ/∂S 分别为表面张力温度和浓度系数;µ为流体动力黏度系数.
3 近似解求解过程
3.1 中心区域近似解
在物理模型中,当深宽比ε→0,有Γ=εδ=ri/l=O(1).为方便计算,无量纲方程中的变量R用 δ+X 代替,则 1/R=1/(δ+X)=ε/(Γ+εX),同时,做如下变换:展开,代入到各控制方程和边界条件中,得到各阶控制方程和相应的边界条件.
零阶控制方程和边界条件如下:
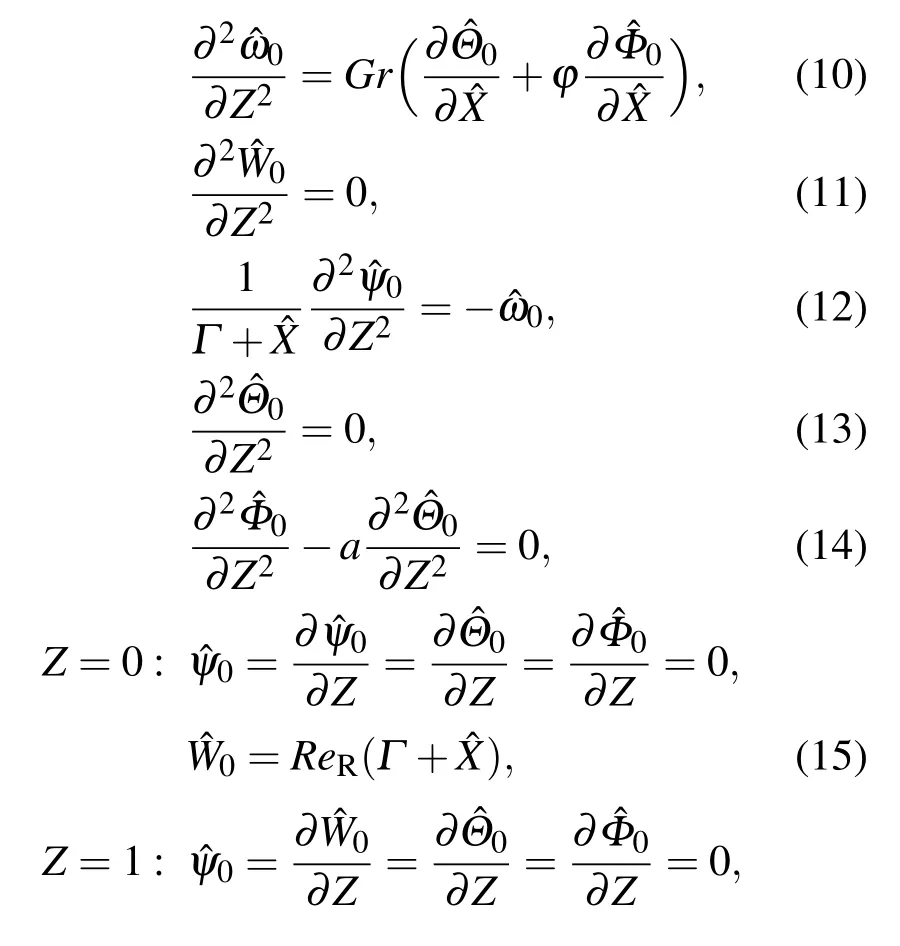

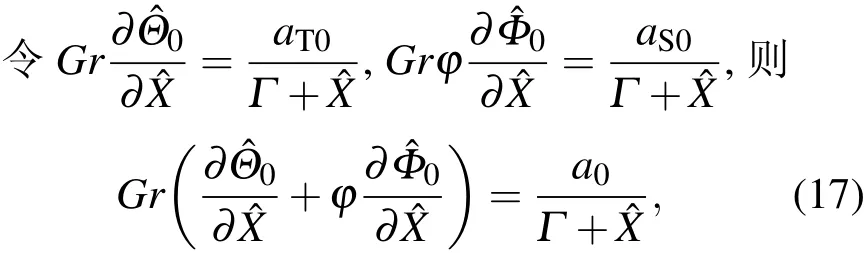
其中a0=aT0+aS0,均为与ˆX有关的参数.由零阶控制方程和边界条件可以求得:
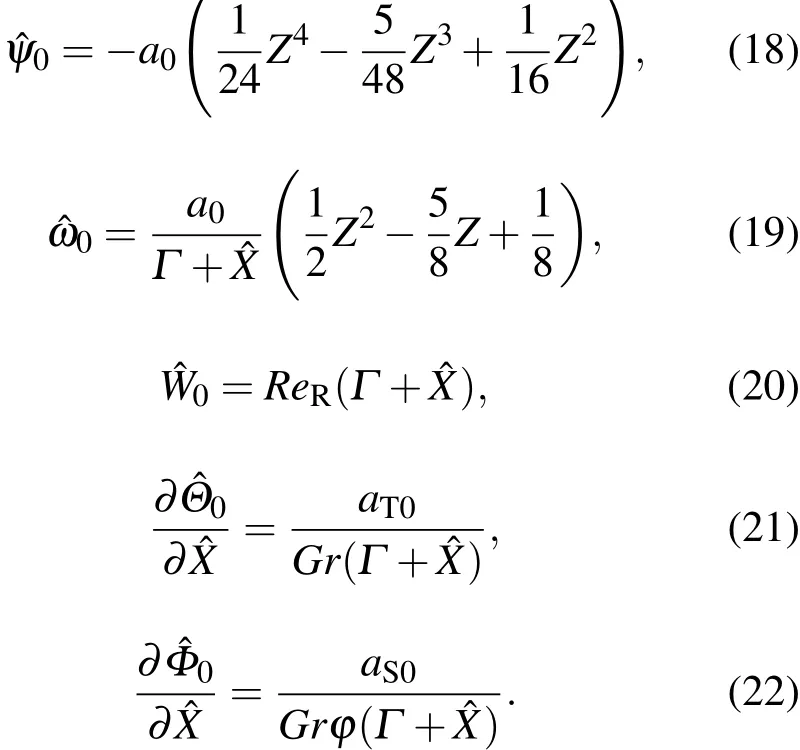
二阶能量方程如下:
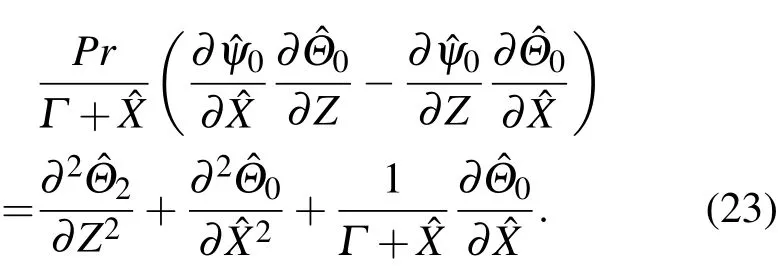
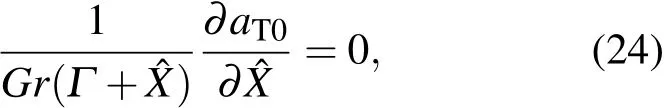
因此,aT0为常数.同理,根据二阶传质方程和边界条件也可证明aS0为常数.
对(21)和(22)式积分得到
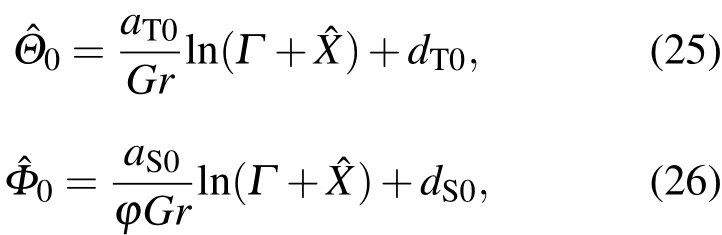
积分常数dT0和dS0在与边界区域的匹配时确定.
运用相同的方法可以求得其余各阶近似解,其中相应的未知积分常数可通过与边壁区域的匹配求得.
3.2 与边壁区域的匹配
边壁区域的无量纲流函数、涡量、周向速度、温度和浓度分别用来表示,为方便起见,做如下变换:则中心区域与边壁区域匹配条件为ε→0时,
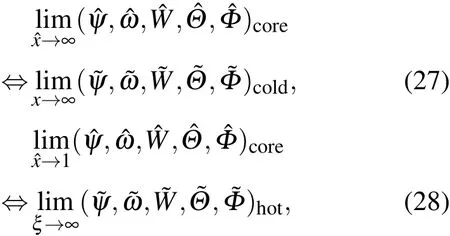
其中ξ=1/ε−X.
由此可以求得:
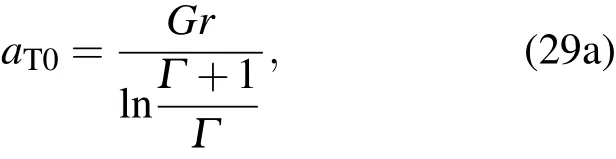
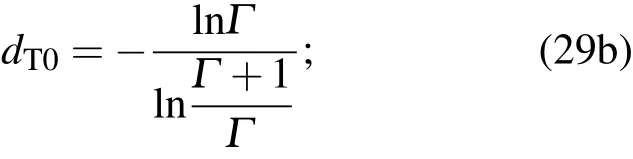
由零阶边界条件得
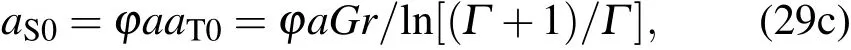
当不考虑Soret效应时,a=0,此时,环形液池内溶质分布均匀,0=0,并且dS0是与a无关的常数,故dS0=0.其他阶中的积分常数亦用相同阶次下的匹配条件求得.
3.3 中心区域解
将各系数代入到中心区域的各阶近似解中,便可完整地写出中心区域的渐近解,结合流函数的定义,可得到中心区域温度、浓度和速度分布为

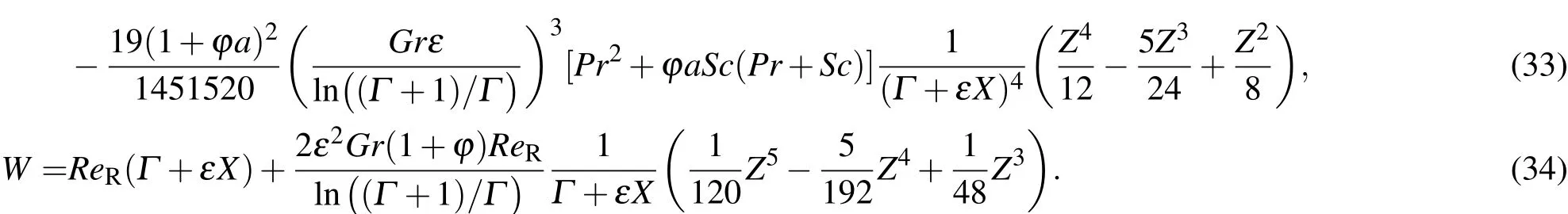
采用此方法可以得到更高阶的解析解,但解的表达式非常复杂,并且ε是一个趋于零的小量,更高阶的项对浅液池内温度、浓度和速度分布的影响很小,可以忽略,所以,这里只给出了二阶近似解析解.
4 结果分析与讨论
当忽略液池旋转及Soret效应时,由于所有固壁无质量渗透,故此时液池内的浓度分布是均匀的,此时的对流过程为无旋转的热毛细-浮力对流过程.在上述解中,令n=0,a=0,则可得到与Li等[21]的研究完全一致的结果.
当忽略浮力时,旋转环形浅液池内耦合热-溶质毛细对流过程相对比较简单,可以采用类似方法求得二阶以上的解.例如,包含三阶的中心区域温度、浓度和速度分布:
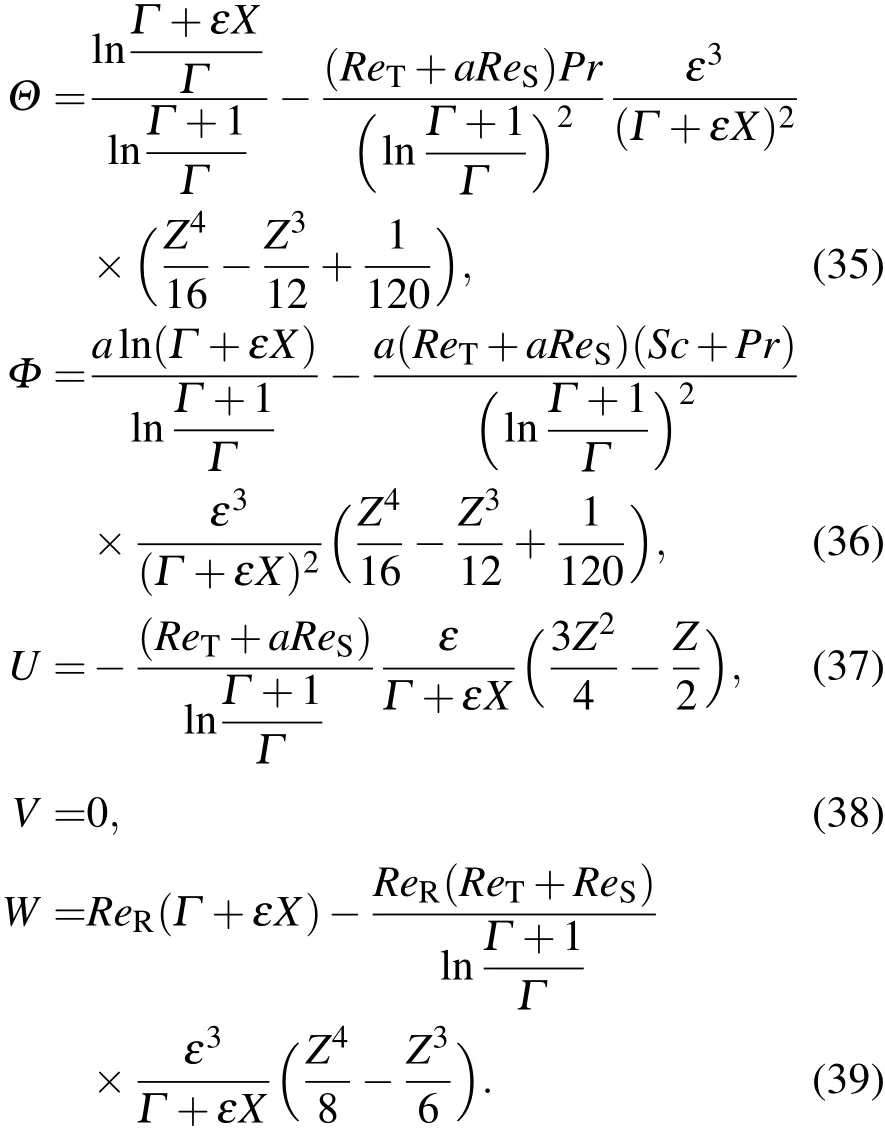
当n=0,a=0时,液池无旋转,且内部溶质分布均匀.上述结果与Li等[20]得到的环形浅液池内纯热毛细对流的近似解完全一致,由此可以证明以上所得结果的正确性.
边壁区域流动结构非常复杂,采用匹配渐近展开法很难求得控制方程在边壁区域的渐近解,根据Leppinen[19],Sen和Davis[23]的研究可知,对于边壁区域的流动结构、温度和浓度分布只能通过数值方法获得.
温度、浓度和速度的分布表达式中不包含旋转雷诺数,它应该包含在更高阶的项中,高阶项对浅液池内的近似解影响很小,可忽略不计,因此,低转速对液池内温度、浓度、径向和轴向速度分布基本没有影响,这与Shi等[13]所研究的旋转环形液池内热毛细对流的结论一致,即较低转速对轴对称的稳态毛细流动过程中的温度和径向速度分布基本没有影响.
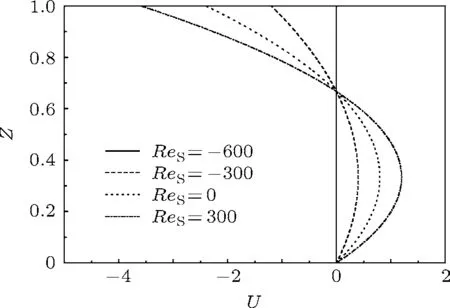
图2 耦合的毛细力对无量纲径向速度分布的影响(ε=1/50,Γ=1/5,Pr=5,Sc=500,Re R=1,Re T=600,Gr=0,φ=0)
为了分析热毛细力、溶质毛细力的耦合效应,进行如下工况的计算:ε=1/50,Γ=1/5,Pr=5,Sc=500,ReR=1,ReT=600,Gr=0和φ=0.图2给出了忽略浮力影响时,耦合热-溶质毛细力对中心截面(R=δ+1/2ε)处流体径向速度分布的影响,当忽略Soret效应时,液池内浓度分布均匀ReS=0,此时为纯热毛细流动过程,自由表面上流体由外壁高温区向内壁低温区流动,回流出现在液池底部附近;当溶质毛细力方向与热毛细力方向相同时,流动增强,否则,流动减弱;当ReS=−600时,热毛细力和溶质毛细力正好相互抵消,流体处于静止状态,因此,速度总是为零.溶质毛细力的大小与Soret效应和液池内初始浓度有关,由浓度差∆S=−DTSSo(1−No)(Th−TC)/D的定义可知,当初始时刻液池内质量分数增大时,Soret效应引起液池内水平方向上溶质浓度梯度增加,溶质毛细力增大,从而增强(热毛细力与溶质毛细力同向)或减弱(两种力反向)流体流动.
图3给出了在温度不均匀引起的浮力恒定的情况下,不同浮力比φ对中心截面径向速度分布的影响.图3中φ=0为忽略浓度不均匀引起的浮力,仅考虑温度不均匀引起的浮力时中心截面上的径向速度分布;φ=−1和φ=1分别表示两种浮力方向相反和相同的情况.对比图2中ReS=600(Gr=0)与图3中的径向速度分布,可以发现:由于耦合的热-溶质毛细力对流体流动起主导作用,浮力对流动强度的影响较小,在计算工况下,由于温度不均匀引起的浮力总是增强流体流动,因此,两种浮力方向相同时,流动增强,方向相反时,流动减弱.
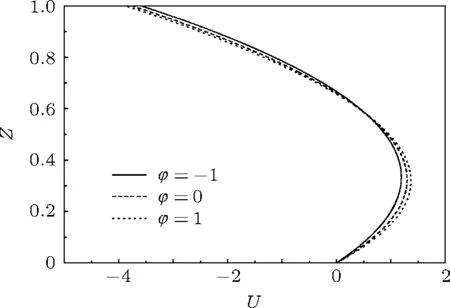
图3 耦合的浮力对无量纲径向速度分布的影响(ε=1/50,Γ=1/5,Pr=5,Sc=500,Re R=1,Re T=600,Re S=300,Gr=10)

图4 施密特数对无量纲径向速度分布的影响(ε=1/50,Γ=1/5,Pr=5,Re R=1,Re T=600,Re S=300,Gr=10,φ=1)
图4 给出了普朗特数Pr恒定时,不同施密特数Sc下中心截面的径向速度分布.毛细雷诺数恒定时,施密特数越大,溶质扩散速率越小,液池内水平方向上Soret效应引起的浓度梯度越小,因此,流动强度随施密特数的增大而减弱.
液池几何尺寸对流动的影响如图5所示,显然,相同的毛细雷诺数下,液池宽度越大,径宽比Γ=ri/l和深宽比ε=h/l越小,液池内水平方向上温度梯度和浓度梯度越小,因此,流动减弱;相反,液池宽度越小,流动增强.

图5 几何尺寸对无量纲径向速度分布的影响 (a)径宽比的影响(ε=1/50);(b)深宽比的影响(Γ=1/5);(Pr=5,S c=500,Re R=1,Re T=600,Re S=300,Gr=10,φ=1)
由以上分析可知:温差引起的表面张力梯度驱动的热毛细对流占主导地位;对于大多数双组分溶液而言,Soret效应相对较小,因此,Soret效应引起的溶质毛细对流相比热毛细对流较弱;浮力对流相比毛细对流更弱;旋转对流动的影响很小,可忽略不计.
5 结论
采用匹配渐近展开法求得了水平温度梯度作用下旋转环形浅液池内耦合热-溶质毛细对流中心区域的近似解析解.结果表明:耦合的热毛细力和溶质毛细力对流动过程起主导作用,低转速和浮力对流动的影响较小,而溶质扩散系数和几何尺寸对流体流动有较明显的影响;当耦合的浮力和毛细力作用方向相同时,流动增强,相反时流动减弱.
[1]Schwabe D,Scharmann A,Preisser F,Oeder R 1978 J.Cryst.Growth 43 305
[2]Cr¨oll A,Mitric A,Aniol O,Sch¨utt S,Simon P 2009 Cryst.Res.Technol.44 1101
[3]Wang J S,Yan J J,Hu S H,Liu J P 2009 Int.J.Heat Mass Transfer 52 1533
[4]Bergman T L 1986 Phys.Fluids 29 2103
[5]Bergeon A,Henry D,Benhadid L H,Tuckerman L S 1998 J.Fluid Mech.375 143
[6]Arafune K,Hirata A 1998 Numerical Heat Transfer A 44 421
[7]Arafune K,Yamamoto K,Hirata A 2001 Int.J.Heat Mass Transfer 44 2405
[8]Chen C F,Chan C L 2010 Int.J.Heat Mass Transfer 53 1563
[9]Li Y S,Chen Z W,Zhan J M 2010 Int.J.Heat Mass Transfer 53 5223
[10]Chen Z W,Li Y S,Zhan J M 2010 Phys.Fluids 22 0341006
[11]Zhan JM,Chen Z W,Li Y S,Nie Y H 2010 Phys.Rev.E 82 066305
[12]Li Y R,Wu C M,Wu S Y,Peng L 2009 Phys.Fluids 21 084102
[13]Shi WY,Ermakov M K,Imaishi N 2006 J.Cryst.Growth 294 474
[14]Zheng L C,Sheng X Y,Zhang X X 2006 Acta Phys.Sin.55 5298(in Chinese)[郑连存,盛晓艳,张欣欣2006物理学报55 5298]
[15]Zheng L C,Feng Z F,Zhang X X 2007 Acta Phys.Sin.56 1549(in Chinese)[郑连存,冯志丰,张欣欣2007物理学报56 1549]
[16]Zhang Y,Zheng L C,Zhang X X 2009 Acta Phys.Sin.58 5506(in Chinese)[张艳,郑连存,张欣欣2009物理学报58 5506]
[17]Cormack D E,Leal L G 1974 J.Fluid Mech.65 209
[18]Merker G P,Leal L G 1980 Int.J.Heat Mass Transfer 23 677
[19]Leppinen D M 2002 Int.J.Heat Mass Transfer 45 2967
[20]Li Y R,Zhao X X,Wu S Y,Peng L 2008 Phys.Fluids 20 082107
[21]Li Y R,Ouyang Y Q,Wang S C,Wu S Y 2010 J.Eng.Thermophys.31 1921(in Chinese)[李友荣,欧阳玉清,王双成,吴双应2010工程热物理学报31 1921]
[22]Li Y R,Wang S C,Wu S Y,Peng L 2010 Microgravity Sci.Technol.22 193
[23]Sen A K,Davis S H 1982 J.Fluid Mech.12 163

