原油管道泄漏扩散影响因素模拟分析

李明，杨威，马一鸣，蔡亮，邹堃

1.中国石油华北油田分公司 第五采油厂（河北 辛集 052360）

2.中国石油大港油田分公司 勘探开发研究院（天津 300280）

3.中国石油东部井控应急救援响应中心（天津 300280)

4.中航油京津冀物流有限公司（天津 300300）

5.中国石油华北油田分公司 经济技术研究院（河北 任丘 062552）

随着经济的迅速发展，我国新建了一系列原油输送管道，但油品在储运的过程中由于腐蚀、第三方破坏和地质灾害等因素影响，当发生泄漏后会在地面形成液池，如点燃形成油池火，不点燃形成可燃气体，严重危害周围人员和设备的安全[1]。因此，研究原油泄漏后油品扩散及液池形成的过程对预防溢油扩散具有重要意义。

目前，国内外的研究方法以实验研究、理论分析、数值模拟为主[2-3]，其中实验研究法由于场地安全方面的考虑，无法完全还原大尺度原油泄漏过程；理论分析通过前提假设并根据质量守恒推导液池面积，但忽略了实际工况中的重要因素。随着计算机技术的发展，数值模拟技术成为此类问题的首选解决方法，宋琳琳等[4]采用计算流体力学（CFD）模拟了埋地原油管道在海泥中的泄漏扩散过程，得到海水流速和油品泄漏速度对油品扩散影响较大；刘雪光等[5]模拟了中缅原油管道在跨越段的油品扩散过程，得到不同工况下油品在江面的扩散形态；史晓蒙等[6]模拟了油品扩散速度与管道压力、泄漏孔径和泄漏时间之间的关系，并进行了实验验证。以上对于油品泄漏的研究具有重要意义，但均为液池在水面、土壤或海泥中的扩散过程，且假设液池为圆柱体，扩散为轴对称，与实际工况不符[7-8]。在此，采用CFD数值模拟技术，模拟原油泄漏后在地面的扩散过程，研究管道内压、泄漏孔径、泄漏速度、地面粗糙度和地面粗糙系数等因素对液池面积的影响，并根据模拟结果拟合液池面积计算公式，为溢油的防控提供参考。

1 数值模拟方法

1.1 几何建模及网格划分

根据某站场内的实际布局建立三维模型，外流体域为空气，区域10 m×10 m×1 m，内流体域为管道，直径0.5 m，中心点距离地面高度0.5 m，泄漏口位于右侧管壁处，泄漏孔径0.1 m。采用Meshing进行非结构化网格划分，并对泄漏口周围和地面进行网格加密，外流体域采用四面体网格，内流体域采用六面体网格，如图1所示，并进行网格无关性验证。随着网格数的增加，液池面积逐渐增大，在超过300万网格后，液池面积变化幅度很小，故确定网格数量为3 001 486。

1.2 数学模型

原油为不可压缩流体，泄漏过程属于自由泄流，故采用标准的k-epsilon湍流模型处理复杂的外部流动进行数值求解，连续性方程和动量方程如下：

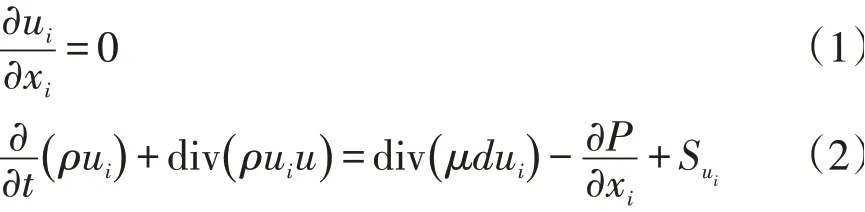
式中：u i为流体沿着x i方向的速度分量，m/s；ρ为流体密度，kg/m3；Su i为湍动能源项；μ为流体黏度，mPa·s；P为管道内压，MPa；t为泄漏时间，s。

采用VOF方法定义每个网格的体积量：

式中：f为每一相的体积分数。

1.3 边界条件及求解方式

设置底面和管道外壁为Wall，泄漏口为速度入口，管道入口、出口和其余壁面均为压力出口，壁面为无滑移，采用基于压力求解器的二阶迎风格式求解。通过改变管道内压、泄漏孔径、泄漏速度、地面粗糙度和地面粗糙系数等，采用单因素模拟对液池面积的影响。

2 结果与讨论

2.1 液池形成过程及模拟验证

在管道内压0.1 MPa、泄漏孔径0.1 m、泄漏速度0.5 m/s、地面粗糙度0.005 m，粗糙系数0.5的条件下，模拟原油泄漏到地面液池的过程，统计横向扩散距离即液池直径，如图2所示。扩散过程分为两个阶段：第一个阶段1~10 s内，初期油品扩散受孔口射流的影响，处于紊态流动，同时泄漏口与地面具有一定高度，在动能和势能的作用下，液池直径呈指数增长，油品与地面碰撞后呈放射状散开；第二阶段10 s以后，射流作用减弱，油品在地面逐渐扩展，此时只受地面摩擦力和液体表面张力的影响，液池直径呈线性增长，随着油品自身重力的增加，液池逐渐铺满整个计算域。

图2 液池直径随时间变化曲线

采用理论计算液池直径，遵守质量守恒定律即一定时间内从泄漏口流出的油品质量与地面上形成液池的油品质量相等，公式如下：

式中：m为泄漏的油品质量，kg；d为泄漏孔直径，m；u为泄漏速度，m/s；t为泄漏时间，s；ρ为油品密度，kg/m3；D为地面形成的液池直径，m；h为液池厚度，m；θ为地面接触角，（°）；ε为地面粗糙度，m；σ为油品表面张力，取0.072 N/m。

对比理论分析计算和数值模拟结果，前10 s内两者的相对偏差在8.2%以内，之后偏差逐渐增大，最大相对偏差为13.11%，这是由于理论分析假设地面为光滑，未考虑地面粗糙均匀程度即地面粗糙系数的影响，从公式（4）~式（5）看也忽略了油品黏度的影响，而CFD模型中可综合考虑多种因素的影响，反应了实际工况条件下油品流动特性，具有较好的可行性。

2.2 管道内压、泄漏孔径、泄漏速度对扩散的影响

考虑到该模拟管道位于站场内，站场内的压力等级较低，因此选择0.1、0.3、0.5 MPa 3个内压等级。在管道内压0.1、0.3、0.5 MPa的条件下，液池面积随时间的变化如图3所示。在相同的时间下，内压越大，液池面积越大，且随着时间的延长，内压对液池面积的影响逐步增大，这是由于液池在地面的扩展速度与内压呈正相关，泄漏油品的动能集中在射流轴线上向前推进，同时油品发生横向扩展。

图3 不同内压对液池面积的影响

在泄漏孔径0.05、0.10、0.20 m和泄漏速度0.25、0.5、1.0 m/s的条件下，液池面积随时间的变化如图4、图5所示。随着泄漏孔径和泄漏速度的增加，液池面积也随之增大。当管道发生小孔、中孔或完全破裂时，一定时间内从泄漏口流出的油品越来越多，在不考虑防火堤和围堰的情况下，在地面形成的液池面积也越来越大。同时根据式（4）也可以看出，液池面积与泄漏速度呈一次相关，与泄漏孔径呈二次相关。

图4 不同泄漏孔径对液池面积的影响

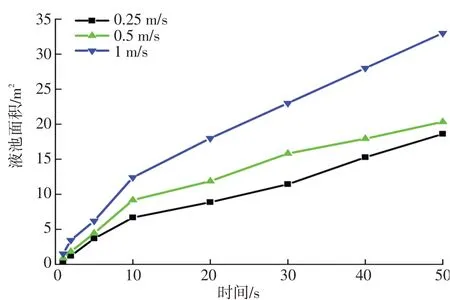
图5 不同泄漏速度对液池面积的影响

2.3 地面粗糙度、粗糙系数对扩散的影响

站场内多以水泥混凝土地面为主，其地面粗糙度不小于0.001 m，故在地面粗糙度0.001、0.005、0.010 m条件下，液池面积随时间的变化如图6所示。液池面积随地面粗糙度的增加而减小，且当地面粗糙度小于0.005 m时，液池面积的变化很小。这是由于当地面粗糙度增加，相当于地面凸起物的平均高度增加，在较大的阻力下，油品向地面四周流散的摩擦阻力增大，流散前锋在向前推进的过程中速度下降，液池厚度增加但面积不再增大。

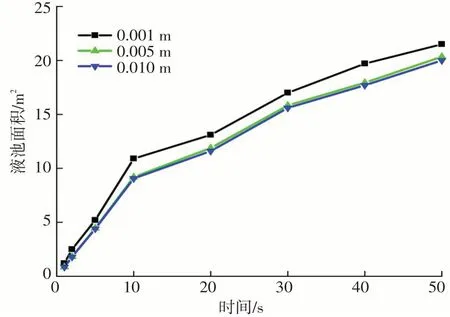
图6 不同地面粗糙度对液池面积的影响

地面粗糙系数代表地面粗糙的均匀程度，在地面粗糙系数0.50、0.75、1.00的条件下，液池面积随时间的变化如图7所示。液池面积随地面粗糙系数的增大而减小，但减小的幅度有限，说明地面粗糙系数对液池面积扩展的阻碍能力有限，这是由于油品溢流到地面后，在流体自身重力和黏滞力的作用下，流散前锋会覆盖地面，此时地面砂粒非均匀性分布对液池的影响远小于砂粒高度，油品对地面产生了足够的润湿。

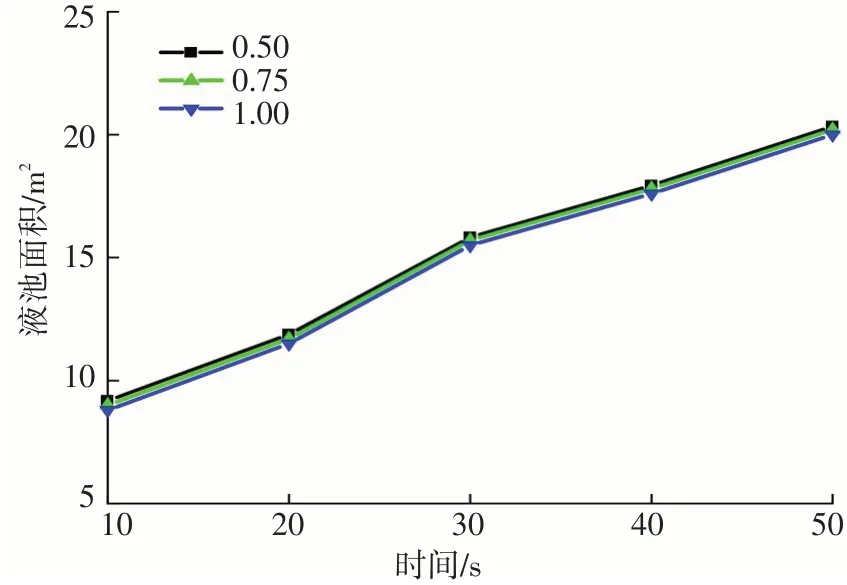
图7 不同地面粗糙系数对液池面积的影响

2.4 油品物性对扩散的影响

目前，我国的原油按照密度和黏度划分为轻质原油、中质原油、重质原油和稠油，见表1。对4种典型油品液池面积随时间的变化进行模拟计算，如图8所示。不同油品发生泄漏后形成的液池面积基本一致，偏差在3%以内，根据FAY理论[9-10]，短时间内的泄漏，液池主要受重力和惯性力的扩展作用，黏性力的影响有限，在密度850~950 kg/m3的范围内形成的液池面积基本一致。

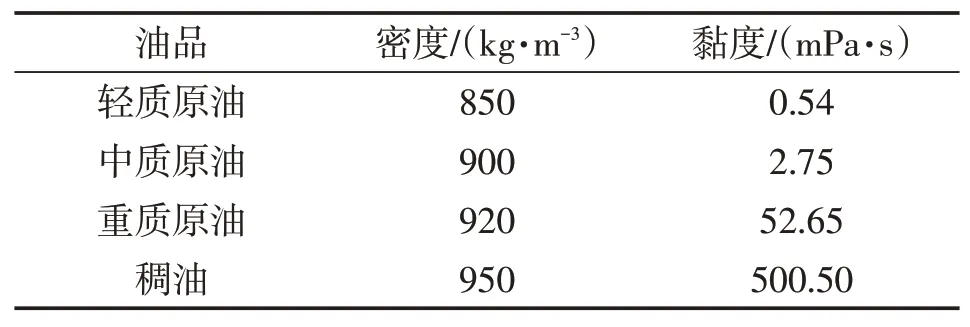
表1 不同油品物性参数

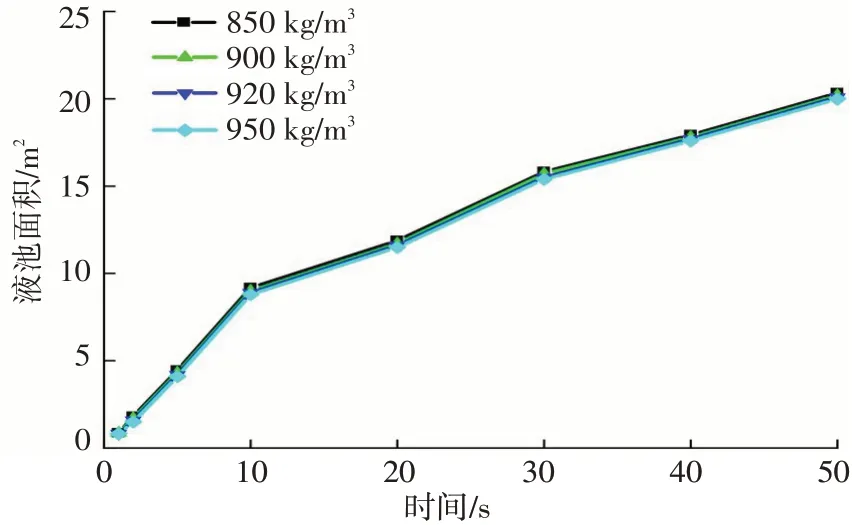
图8 油品物性对液池面积的影响

3 数据拟合

根据单因素影响分析，液池面积与管道内压、泄漏孔径和泄漏速度呈正相关，与地面粗糙度呈负相关，地面粗糙系数和油品物性对液池面积的影响较小，因此建立液池面积与相关因素的关系式，结合量纲齐次定理，采用Origin 2019b进行非线性拟合，公式如下：

式中：S为液池面积，m2；ε为地面粗糙度，m；P0取0.1 MPa，d0取0.1 m，u0取0.5 m/s；A、B、C、D为待定系数。

拟合后方程为：

将CFD的模拟结果和公式（7）的计算结果进行对照，如图9所示，两者相对误差在10%以内，证明拟合方程的准确性较高，可以用来预测油品泄漏后形成的液池面积。

图9 CFD模拟结果和拟合公式结果对比

4 结论

1）CFD模拟综合了各种因素的影响，可反应实际工况条件下油品流动特性，数据结果具有很好的吻合性。

2）在泄漏的过程中，液池面积随管道内压、泄漏孔径和泄漏速度的增大而增大，随地面粗糙度的增大而减小，且在地面粗糙度小于0.005 m时，液池面积基本不变，地面粗糙系数和油品物性对液池面积的影响较小。

3）根据量纲齐次定理，对数据进行非线性曲面拟合，其计算值与模拟值相比相对误差在±10%以内，说明计算关联式可以作为液池面积的预测公式，为溢油防控提供理论依据。