混沌映射和神经网络互扰的新型复合流密码*

陈铁明 蒋融融

1)(浙江工业大学计算机科学与技术学院,杭州 310023)

2)(浙江广播电视大学信息与工程学院,杭州 310013)

(2012年3月31日收到;2012年9月28日收到修改稿)

1 引言

混沌是物理、数学、非线性动力学等多学科交叉的一种新理论,混沌系统的“蝴蝶效应”和“不确定性”已在密码学领域引起广泛关注.混沌系统所具有的基本特性可满足保密通信及密码学的基本要求:混沌动力学方程的确定性保证了通信双方在收发过程或加解密过程中的可靠性;混沌轨道的遍历性正好满足密码系统设计的扩散原则;混沌参数和初值敏感性正好满足密码系统设计的混乱原则[1].与传统密码相比,混沌密码具有结构简单、容易实现、安全高效等特点[2],可构建随机数发生器[3]、流密码[4]、分组加密[5]、公钥加密[6]等方案,其中以流密码的研究与应用最为普遍[7,8].当前对混沌流密码的研究主要集中在多混沌系统互扰复合的方法[9],但最近有国内学者提出了混沌流的随机性和混沌映射弱密钥的随机性测量等问题[10,11],说明多混沌的复合未必能构建随机性更好的混沌密钥流.因此,寻求传统混沌与其他随机模型互扰的复合方案或将成为流密码研究突破的新方向.

神经网络也是一种高度非线性的动力学系统,因此将混沌和神经网络相结合的研究也受到人们关注,形成了混沌神经网络的研究分支[12],但目前尚未出现将神经网络与混沌系统互扰构建流密码的研究成果.最近的研究表明,两个权值不同、输入同步的神经网络模型通过输出位交互学习,最终可实现两个权值向量的同步状态[13],该权值同步可被利用在公开信道上构建密钥协商方案,即双方预先共享输入向量且保持同步的随机变化,则通过输出位不断更新各自的权值向量,最终可在有限步交互后实现权值向量的同步,将同步的权向量映射为会话密钥即可完成通信双方的密钥协商[14].

我们称上述的权值同步神经网络模型为奇偶树型机(tree parity machine,TPM).由分析知,两个TPM输入的动态随机性是实现两个权值同步的基本保障[15],因此可将混沌系统产生的随机序列引入作为TPM的输入;另外,TPM在权值同步后,只要两边的输入保持动态变化,两边的权值也将动态保持同步状态,因此已有研究提出了基于TPM同步权值映射的流密码方案[16].

综上所述,本文将研究一种TPM和混沌系统融合互扰的新型复合流密码方案,即首先利用混沌映射产生的随机序列作为TPM的输入,当实现TPM权值同步后,将同步权值映射为随机序列与多个混沌系统复合,最终产生混合随机的密钥流.

2 新型复合流密码方案

2.1 理论基础知识

2.1.1 混沌映射模型

这里考虑一种常见的Logistics混沌系统,其映射函数如下:

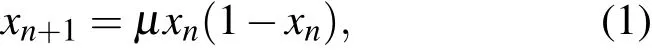
当参数µ落在区间[3.56999456···,4]时,Logistics映射的迭代值xn可进入混沌态.已有的研究已从理论和实验角度充分论证了Logistics映射用作随机数发生器的可行性及较线性反馈移位寄存器(LFSR)等传统随机数发生器的优点.Logistics映射通常将初始状态x0作为密钥,由于对初始值的敏感性,即使解密密钥x只是与x0存在微小差异,迭代后产生的混沌序列也会明显不同,从而保障流加密应用的安全性.

Logistics映射只包括乘法和减法运算,易于计算机程序实现.但由于计算机数据处理的精度有限,可能造成系统的混沌特性退化,因此多混沌复合是一种有效抵抗数字混沌特性退化的有效方法.例如,用两个混沌系统作为随机数发生器,通过两个系统的输出决定最终的密钥流输出,或引入线性同余序列(LCS)与三个Logistics映射的组合方式,延长混沌序列的周期等.

2.1.2 神经网络互学习模型

记一个基本的单层神经元的输入向量X为在区间[0,1]上服从高斯分布的N维输入向量,W为正交规范化的N维权向量,σ代表取值仅为+1或−1的神经元输出值.

记两个交互学习的神经元分别为A和B,则XA,XB和WA,WB分别代表A和B的输入向量和权值向量.进一步将权值的取值离散化在整数区间[−L,L]上(权值边界L为一正整数)、输入向量的元素取值为+1或−1,并满足每次交互学习后输入向量都随机变化但始终保持XA=XB,即保持同步随机变化.两个神经元通过交换各自的输出值实现交互学习,目的是更新各自的权值向量(初始权向量由双方各自随机产生).权值更新规则如下:

权值更新的条件为:σA(t)=σB(t),且满足:w=L(w＞L)或w=−L(w＜−L),其中w∈WA(B).

其中,输出值为 +1或 −1,依赖于权值向量和输入向量内积的符号函数,即σA(B)=这里的sign()函数定义为

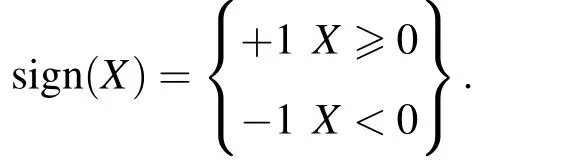
下面给出TPM模型.TPM是在上述单层神经元基础上含多个隐藏单元的多层树型神经元复合网络,网络的最终输出值由一个关于所有隐含层输出值的函数确定,记τA(B)=K为隐含层个数.

由于隐含层的输出值只能取+1或−1,为了使TPM的输出值也取+1或−1,可将输出累积函数 f设置为所有隐含层输出值的乘积.因此,若假设TPM包含K个隐含单元,每个隐含单元拥有N维随机输入向量,记第k个单元的输出为σk(t),则TPM最终的输出值可表示如下:

进一步,对K个隐含层神经网络的一种权值更新规则设置如下:

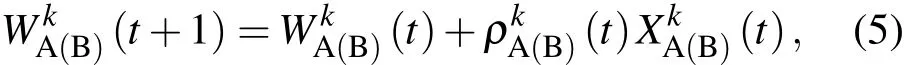
其中,

我们在文献[15]中详细阐述了一种TPM交互学习权值同步模型.

2.2 TPM与混沌系统的互扰复合模型

考虑TPM工作时需要一个输入随机数发生器,可采用混沌映射产生的序列作为TPM输入流,且混沌系统的轨道确定性可保证双方随机输入的同步.更进一步,为确保TPM输入的随机性,可采用具有多个不同初值的混沌映射分别作为TPM中多个隐含层的输入序列发生器.因此,若采用参数为K,N,L的TPM,则需使用K个初始状态不同的Logistics映射分别作为K个隐含层神经元节点的输入源,两个TPM交互学习达到权值同步后,将K个混沌映射复合后与TPM同步的权值互扰,最终形成随机的混沌密钥流.根据文献[15]的分析结果,采取常用的K=3的TPM模型,则上述的流密码系统整体结构如图1所示.

系统初始化时,流密码系统两端分别为同参数结构的TPM随机生成两个权值向量,两边分别利用同结构的混沌映射为TPM产生相同的随机输入序列,同时执行TPM交互学习过程,最终可实现双方的权值同步.整个过程仅需交互传输TPM的若干输出值,TPM的内部输入和内部权值均不会在公开的网络信道中传输.利用系统两边同步的TPM权值,还可实现对两边各个混沌映射初始值的更新,以便产生新的动态输入序列,而基于动态的TPM同步输入序列,TPM也将保持同步权值的动态更新.因此,图1所示的混沌流密码系统具备了密钥管理功能,其中XOR表示随机序列的异或操作.在实际应用中,混沌映射的参数更新方式较为灵活,可根据定时间或定流量等方式具体确定.

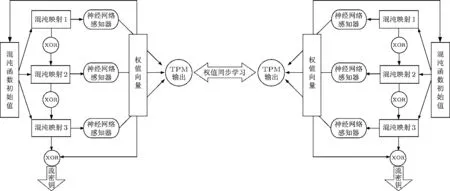
图1 基于TPM和多混沌映射互扰复合的流密码系统基本结构

图2 三个Logistics映射和一个TPM复合的密钥流生成器

三个Logistics映射和一个TPM同步权值向量的互扰复合密钥流结构如图2所示.显然,K=3的TPM模型的权值向量元素个数为3N,则通过对各个权值的累积和施行sign()函数后,与三个Logistics映射产生的迭代值xi在异或作用下生成密钥流序列Ki.对于每个Logistics映射每次产生一个新的迭代值,两边同步的TPM权值将相应更新,最终在互扰复合的方式下将不断产生新的密钥序列.

3 性能测试与效果分析

3.1 TPM权值同步的性能测试

TPM交互学习达到权值同步依赖于输入的随机性,下面分析TPM输入的随机数发生器采用混沌序列和常见的LFSR两种情况下的权值同步性能.选定TPM参数N=100,K=3,L=3,分别用LSFR和Logistics映射作为输入向量的随机数发生器(分别记为TPMFSR和TPMChaos).考察两种情况下实现TPM权值同步所需的平均交互次数,每次权值同步的实验执行1000次取平均值,15次独立实验的权值同步平均交互次数如图3所示.

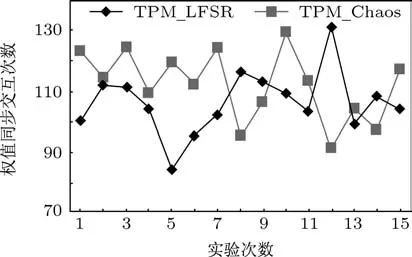
图3 基于不同随机数发生器的TPM权值同步所需的平均交互次数

3.2 互扰复合序列的随机性测试

在由图2结构产生的TPM混沌序列中随机选取长度为10000 bit的若干不同子序列,统计子序列中所有比特位上1的个数,24次独立实验的统计结果如表1所示.可以看到,序列中每个比特位上0和1出现的概率均接近50%,满足伪随机序列的最基本要求.

表1 混沌随机子序列中1出现的次数统计表

美国国家标准技术研究所(NIST)制定了一整套序列随机性检测标准[17],其中的测试从不同角度对待测序列与理想随机序列的偏离程度做出评估.本文选取如下几项测试指标.

1)单比特频度测试(frequency monobit test):测试整个序列中0和1各自的比例,判断其与理想随机序列的偏差.

2)累积和测试(cumulative sums test):测试子序列的累积和的最大值与理想随机序列的偏离程度.子序列的累积和通过修正后的(−1,1)序列计算得到,测试分为前向(forward)和后向(backward)两种.

3)游程测试(runs test):测试序列中的游程(连续的0和1的长度)的总数,判断其与理想随机序列的偏差.

4)离散傅里叶变化测试(discrete fourier transform spectral test):测试序列傅里叶变化的峰值,检测其周期特性与理想随机序列的偏离程度.

5)近似熵测试(approximate entropy test):测试两个相邻长度的子序列发生重叠的概率,近似熵是一种判断序列复杂度大小的准则.

所有测试从待测序列中抽取一段子序列,根据不同测试计算出一个相应的p值,当p≥α时,认为序列通过随机性检测,其中α为显著水平,NIST测试套件中的默认值为0.01.

本文选取了单个的Logistics映射(记为Log),三个Logistics映射的异或叠加(记为3Log),文献[18]提出的三个Logistics映射与一个线性同余式的组合(记为LCS3Log),以及本文提出的三个Logistics映射和一个TPM的组合(记为TPM3Log),分别产生一段100 Mbit的序列作为测试源.测试选取的随机子序列长度为1 Mbit.测试结果如表2所示.

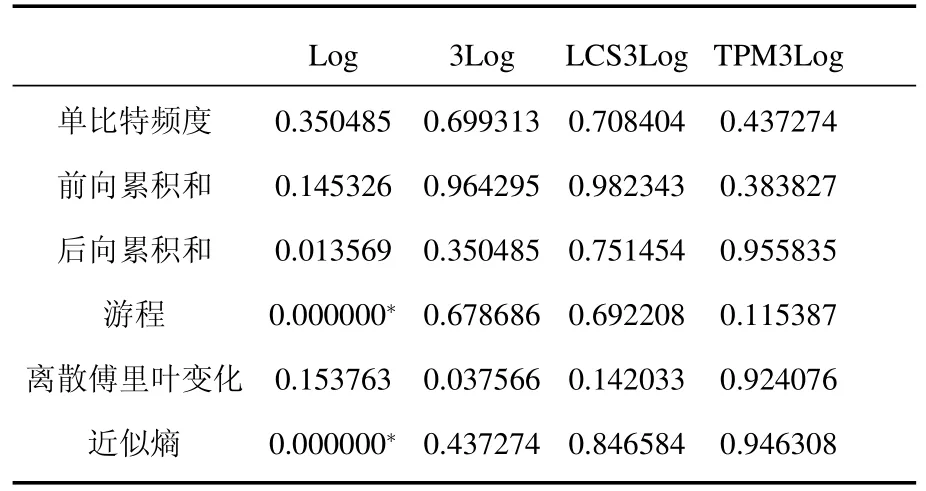
表2 各种混沌密钥流的随机子序列p值检测结果对比

测试结果表明,使用单个Logistics映射所产生的序列难以满足较高的随机性要求,而本文提出的TPM3Log方案通过了所有测试,产生的序列具有较好的随机性,另外两种方案同样通过了测试.

对通过上述测试的三种方案,进一步随机选取100段子序列重复测试,测试结果如表3.表中的p值表征子序列的p值分布,通过测试的下限值为0.0001,通过比率是指100个子序列中通过p值检验的序列个数,理想值大于96.

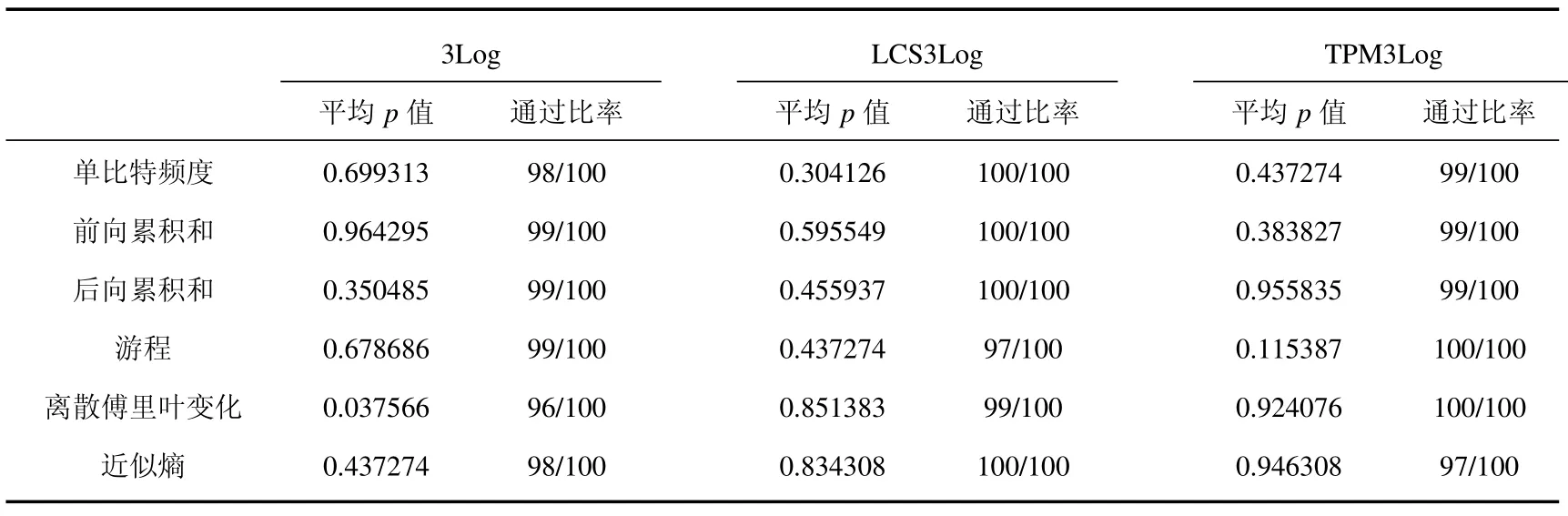
表3 各种混沌密钥流中100段子序列p值分布检测结果对比

根据文献[17]提出的两种经验主义判断准则,对于一个理想随机序列,其子序列测得的p值除了应满足一定的通过率外,还要在[0,1]区间内呈现均匀分布.由表3的测试结果表明,LCS3Log与TPM3Log两种方案下的序列随机性明显优于简单的Logistics叠加(3Log),而在大多数情况下,本文提出的TPM3Log所产生的序列具有更好的p值分布特性.

3.3 图像流加密应用效果

下面给出用TPM3Log产生的密钥流对图像加解密的应用实例分析.系统结构如图4所示,密钥流发生器根据密钥K产生随机序列Keystream,原始图像P通过Keystream序列加密后产生密文C,接收端首先由K′产生随机序列Keystream′,并对收到的密文C′进行解密.其中的加解密过程均为异或操作,当且仅当双方的密钥相等,即K=K′时,图像才能被正确解密恢复.

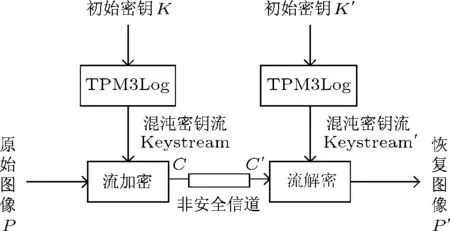
图4 基于混沌流密码的图像加密应用系统示意图

加密选取的原始图像如图5(a)所示.为消除初始混沌过渡态的影响,选取迭代10000次后的TPM3Log序列值作为图像加解密的密钥流序列,得到加解密结果如图5(b)和(c)所示.此外,将解密密钥最低比特位取反,即对密钥进行微小变动,得到错误解密结果如图5(d)所示,体现了流密码应用系统对初始密钥的极端敏感性,即任何微小错误的密钥都会导致图像的大规模恢复失败,且攻击者无法从错误图像中获取原始图像的必要信息.

通过比对原始图像及加密后图像的灰度直方图(图6(a)和(b))发现,经过TPM3Log序列加密后,图像的各像素点在灰度值上分布更为均匀,说明该流加密应用系统可极好地掩盖原始图像的灰度统计信息.

4 结论

在实际应用领域,多混沌系统的互扰复合流密码是一种加强流密钥安全性的常用方法.本文将TPM新型神经网络互学习模型引入到多混沌复合的流密码系统中,具体将三个Logistics映射产生的混沌序列分别作为包含三个隐含层神经元的TPM的随机输入,两边的TPM根据输出值经若干次交互学习且不断更新权值后,可实现两个内部权值向量的同步,将同步的权值做映射处理后即可形成一个新型的随机序列发生器,最终将上述一个TPM同步权值产生的随机序列和三个Logistics映射产生的混沌序列复合,构成一个新的流密钥发生器.实验分析表明,新的流密钥比一般的多混沌复合流密钥具有更好的随机性,应用于数字图像加密[19−22]效果好.

事实上,混沌同步保密通讯系统还面临相空间重构、混沌信号流回归分析、同构混沌系统广义同步等攻击[23−25].本文提出的混沌流密码通过两个操作增强了安全性:1)采用多混沌序列和神经网络同步序列的混合;2)支持混沌初始参数的动态更新.多个Logistics映射序列与TPM混合产生的混沌密钥流可有效抵抗相空间重构等方法对同步混沌信号的直接提取攻击,同时可消除混沌特性的数字退化问题;利用TPM同步的权值实现对多个Logistics映射的参数更新则可有效增强对混沌系统初始参数的猜测攻击难度,据此还可进一步研究动态的密钥管理方案,使新型的混沌流密码更具有实用价值.

图5 图像加解密结果 (a)原始图像;(b)加密后图像;(c)正确解密图像;(d)错误解密图像

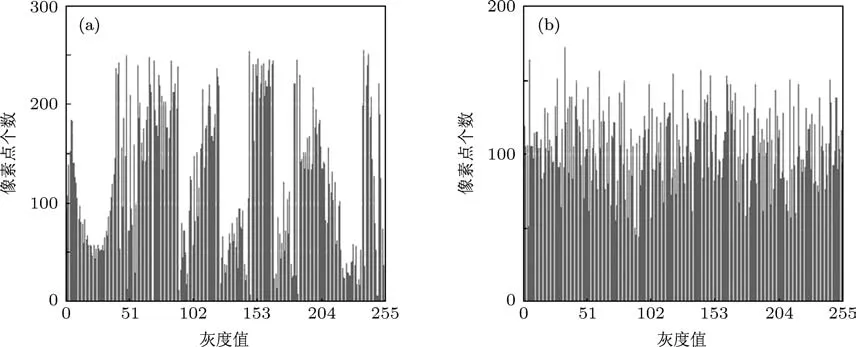
图6 图像灰度值统计特性 (a)原始图像灰度直方图;(b)加密后图像灰度直方图

[1]Alvarez G,Li S 2006 Int.J.Bifurcat.Chaos 16 2129

[2]Dachselt F,Schwarz W 2001 IEEE Trans.Circ.Syst.I 48 14

[3]Stojanovski T,Kocarev L 2001 IEEE Trans.Circ.Syst.I 48 281

[4]Li S,Mou X,Cai Y 2001 Second International Conference on Cryptology in India,Chennai,India,December 16–20,2001 p316

[5]Xu S J,Wang J Z 2008 Acta Phys.Sin.57 37(in Chinese)[徐淑奖,王继志2008物理学报57 37]

[6]Ariffi n M,Abu N 2009 Int.J.Crypt.Res.1 1490163

[7]Li W,Hao JH,Qi B 2008 Acta Phys.Sin.57 1398(in Chinese)[李伟,郝建红,祁兵2008物理学报57 1398]

[8]David A,Gonzalo A,Li S 2011 Commun.Nonlinear Sci.16 805

[9]Xiang F,Qiu S S 2008 Acta Phys.Sin.57 6132(in Chinese)[向菲,丘水生2008物理学报57 6132]

[10]Chen X J,Li Z,Cai J P,Bai B M 2011 Acta Phys.Sin.60 064215(in Chinese)[陈小军,李赞,蔡觉平,白宝明2011物理学报60 064215]

[11]Yin R M,Yuan J,Shan X M 2011 Sci.China Informat.41 777(in Chinese)[尹汝明,袁坚,山秀明2011中国科学:信息科学41 777]

[12]Aihara1 K,Takabe T,Toyoda M 1990 Phys.Lett.A 144 333

[13]Wolfgang K,Kanter I 2002 Solid State Phys.42 383

[14]Chen T M,Cai J M,Ma S L 2011 China Commun.8 118

[15]Chen T M,Huang S H,Liu D,Cai JM 2009 J.Comput.Res.Develop.46 1316(in Chinese)[陈铁明,Samuel H Huang,刘多,蔡家楣2009计算机研究与发展46 1316]

[16]Markus V,Sebastian W 2005 IACR Cryptology ePrint Archive 2005 232

[17]Rukhin A,Soto J,Nechvatal J 2001 NIST Special Publication 800-22 13

[18]Chen S,Zhong X,Wu Z 2008 Sci.China F Informat.Sci.51 1055

[19]Wang Z,Huang X,Li N,Song X N 2012 Chin.Phys.B 21 050506

[20]Yuen C H,Wong K W 2012 Chin.Phys.B 21 010502

[21]Sun F,L¨u Z W 2011 Chin.Phys.B 20 040506

[22]Zhu C X,Sun K H 2012 Acta Phys.Sin.61 120503(in Chinese)[朱从旭,孙克辉2012物理学报61 120503]

[23]Perez G,Cerdeira H 1995 Phys.Rev.Lett.74 1970

[24]Wang X,Zhan M,Lai C H,Gang H 2004 Chaos 14 128

[25]Wang X Y,Xie Y X,Qin X 2012 Chin.Phys.B 21 040504