耦合分数阶布朗马达在非对称势中的输运*

王飞 邓翠 屠浙 马洪†

1)(四川大学数学学院,成都 610064)

2)(电子信息控制重点实验室,成都 610036)

(2012年7月17日收到;2012年9月20日收到修改稿)

1 引言

关于布朗马达[1]问题的研究,最初是源于热力学中有关第二类永动机问题的争论,以及希望对一些复杂的输运机制给出合理解释.以往的研究大多集中于对单个布朗马达输运机制的分析[2,3],但在许多情况下粒子之间的相互作用是不可避免的,甚至有时起着决定性作用.最近二十年,在对耦合布朗马达的研究中,发现耦合能够促使粒子链有更快的平均流速[4,5],而驱动力频率对粒子链的运动方向也有显著影响[6],并且在对称周期势下粒子链也能产生定向输运[7,8]等.随着分子操纵技术的发展,耦合布朗马达的定向输运问题开始受到化学和生物学等不同学科领域的密切关注[9,10].在化学方面,应用Frenkel-Kontorova(FK)模型研究了链状分子十六烷的输运现象[11];在生物学的分子马达研究中,发现许多稍大的分子马达实际具有复杂的内部结构,即具有如双头和多头肌动蛋白马达这样的多自由度特殊结构,多个这样的分子马达相互作用时就会产生复杂的输运现象[12,13].但目前关于耦合布朗马达输运现象的研究仍大多局限于整数阶动力系统[1−13].

越来越多的研究表明,粒子在黏性介质中的运动具有“记忆性”,这是整数阶动力系统难以刻画的,而近年迅速发展起来的分数阶随机微分方程理论,则特别适合于描述具有记忆、遗传和路径依赖性的物理、化学和生物学现象[14,15],为研究耦合布朗马达在具有“记忆性”黏性介质中的输运现象提供了崭新的数学工具.

本文应用分数阶FK模型研究粒子链在黏性介质中的定向输运现象.通过数值模拟,观察到整数阶动力系统情况下所没有的定向输运反向流;此外,还讨论了阶数、耦合强度和噪声强度分别对粒子链的平均流速的影响,发现当固定噪声强度时,粒子链的平均流速随耦合强度、阶数的变化会产生广义共振;而当阶数固定时,粒子链的平均流速则会随噪声强度的变化出现广义随机共振现象.

2 模型建立

2.1 经典的FK模型

考虑经典的FK模型[16,17],如图1所示,周期长为l的棘齿势V(x),在外力yi(t)和噪声的驱动下,忽略惯性效应,系统运动方程为

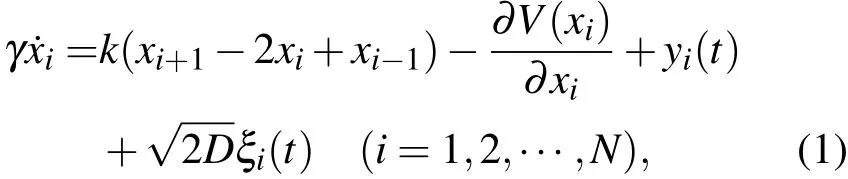
其中k为耦合强度,D为噪声强度,设粒子间自由长度为a,不显含于上式,γ为阻尼系数,为方便通常设 γ=1,ξi(t)为高斯白噪声:〈ξi(t)〉=0,

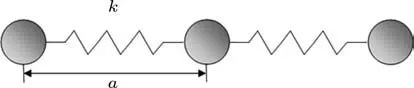
图1 FK模型原理图

2.2 分数阶FK模型

然而在很多物理和生化环境中,黏性介质对速度通常具有幂律记忆性:距当前时刻越近,记忆性越强;距当前时刻越远,记忆性越差.描述这种退色记忆性的阻尼核函数γ(t)为[21]

为方便通常设γ0=1.

由图2可以看出,γ(t)随着时间t的增加按t的幂次逐渐衰减,α越大γ(t)衰减越快,α越小γ(t)衰减越慢.

把(3)式带入(2)式得到

根据Caputo分数阶微积分的定义[22,23],上式可以写为

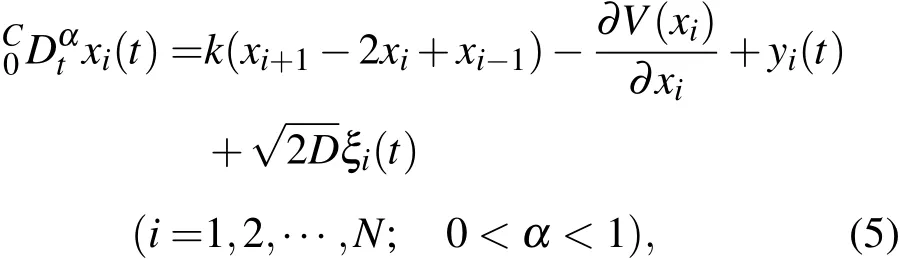
称(5)式为分数阶FK模型.

图2 分数阶阻尼核函数γ(t)

2.3 模型说明

这里所关心的重点是耦合系统粒子链的平均流速[5],定义如下:

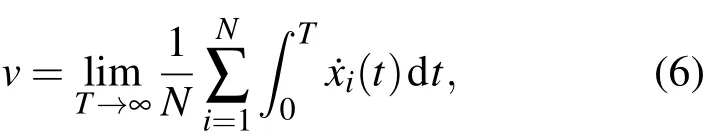
其中N是系统中的粒子数,T为总时间.平均流速是一个宏观物理量,反映了粒子运动的一个整体趋势.

图3 势函数V(x)示意图

我们选用一个周期l=1的棘轮势,形式为

V(x)的示意图如图3.

对外力yi(t),要求满足〈yi(t)〉=0,即外力无偏置.这里主要考虑yi(t)为对称的周期力

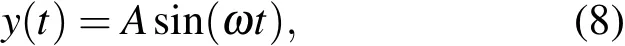
其中A为周期力幅度,ω为周期力的角频率.

3 数值模拟

当粒子间没有相互作用,即k=0时,系统转化为外力作用下的单粒子在棘轮势中的运动;当粒子间相互作用趋于无穷大,即k→∞时,所有粒子都被刚性束缚在一起,系统的动力学行为相当于单个粒子在有效势中的运动[5].本文排除上述极端情况,主要考虑对于有限大小的耦合强度k,粒子间的相互作用所引起的复杂定向输运行为.

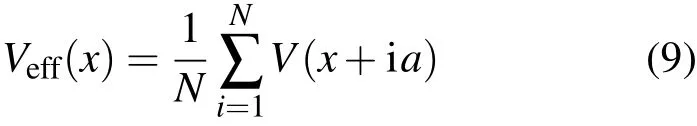
为了模拟方程(5)所刻画的粒子运动,我们采用分数阶差分法[22].采样步长∆t=0.005 s,仿真时间取50 s,粒子数N=10,角频率ω=1,噪声强度D=0.1,采用周期边界.

需要指出的是,粒子xi在时刻t受到的阻尼力即t时刻的阻尼力是时段[0,t]内的速度关于阻尼核γ(t)的加权平均.当阶数α→1时,即系统的记忆性变差,核函数γ(t)的衰减加快,这意味着历史速度对当前阻尼力贡献减少,阻尼力变弱,导致粒子具有更快的输运速度;而当阶数α降低时,即系统的记忆性增强,历史速度对当前阻尼力贡献增强,阻尼力也随之增强,致使定向输运的速度减缓,甚至当这种记忆性增强到某一程度时,促使粒子反向越过势垒,形成定向输运反向流.

对不同强度的周期力和不同大小的耦合强度,图4给出了平均流速v与阶数α的关系.

图4 不同耦合强度和周期力幅度下,粒子链平均流速v与阶数α的关系 (a)k=0;(b)k=3;(c)k=5;(d)k=10

在周期力强度较弱时(A=0,1),小周期力不足以使得单个粒子越过势垒,粒子只能在势阱中徘徊.当粒子间不存在相互作用,即k=0时,众粒子的运动不能相互协调,各粒子在时刻t所受阻尼力的方向也不尽相同,即使较小的阶数α导致历史速度对当前阻尼力贡献较强,也不足以使得单个粒子越过势垒形成定向输运;但若粒子间存在相互作用,即k＞0时,耦合使得粒子间的运动相互协调,各粒子在时刻t所受阻尼力也就具有较大的同向分量,加之小周期力和噪声的作用,这样当阶数足够小时,粒子链将形成定向输运反向流.

在受到较强的周期力时,周期力能促使单个粒子越过势垒.我们观察到,若阶数α→1时,系统的记忆性变差,有正的定向流出现;但当α→α0(α0为v(α)与横坐标交点所对应的阶数,参见图4)时,系统的记忆性增强导致粒子运动的阻尼力增强,平均流速v将减小并趋于0;随着阶数α继续减小,将会出现定向输运反向流,并在负方向上出现一个共振峰值.对于不同的周期力强度,发现在A=5的时候,对应着较大的正向平均流速,说明系统在阶数和耦合强度固定时,存在一个使粒子链平均流速极大的A.并且对于具有较大正向平均流速的A,要使系统出现定向输运反向流的阻尼力也应较大,因此对阻尼力有实质贡献的历史时间需要更长,也就是对应于更小的α0;而当周期力幅度A相同时,随着耦合强度k的增加,α0也增加.

对不同的阶数α,图5给出了周期力幅度A=2.3时,平均流速v与耦合强度k的关系.当α=1和0.8时,可以明显观察到正向上的共振曲线,即在某一优化耦合强度下系统存在正向极大平均流速.随着阶数下降到0.5,系统记忆性增强,系统产生了反向流,并随k增加,在负向上出现了共振曲线,即在k≈3时,粒子链存在负向极大平均流速.这组曲线表明:太弱的耦合不能使得粒子之间形成统一的跃迁;太强的耦合,所有粒子束缚在一起,同样限制了粒子链的输运;适当的耦合强度可以使粒子链的输运速度达到极值.

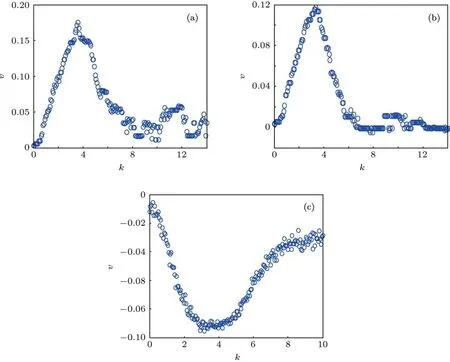
图5 不同阶数下,粒子链平均流速v与耦合强度k的关系 (a)α=1.0;(b)α=0.8;(c)α=0.5

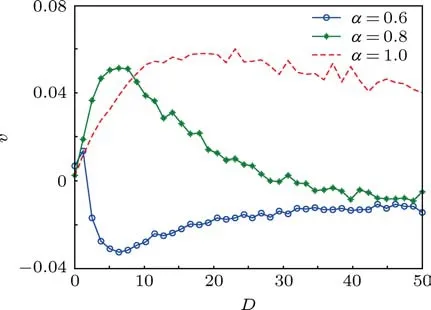
图6 阶数固定情况下,输运速度v与噪声强度D关系

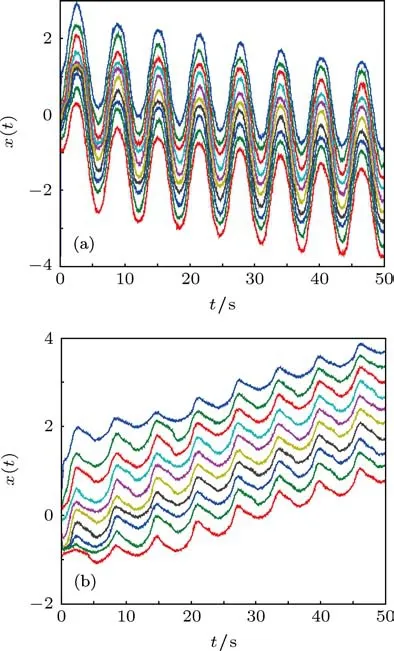
图7 不同阶数下,各粒子平均位移随时间的演化 (a)α=0.6;(b)α=0.8

固定A=1.6,k=3,图6展示了平均流速v与噪声强度D的关系.我们发现当阶数为1时,系统不具有记忆性,平均流速v在正向上产生了广义随机共振现象.当α=0.8时,系统记忆性较弱,观察到了与整数阶情况相同的现象,但在噪声强度较弱的时候(D＜8),平均流速明显快于整数阶情况,这主要是由于在具有记忆性的系统中,历史速度对当前阻尼力有贡献,而历史速度受到历史噪声的影响,因此历史噪声间接地对当前速度做出贡献,所以较之整数阶情况,达到极大平均流速所需要的噪声强度明显下降.而当阶数减少到0.6时,系统记忆性再增强,平均流速v随噪声强度D的增加在负向上产生了广义随机共振现象.

固定噪声强度D=5,图7给出α分别为0.6及0.8时,各粒子平均位移〈xi(t)〉的时间演化.可以明显地看出,当α=0.6时粒子整体向负方向运动,而α=0.8时粒子整体向正方向运动.这同样证实了前文的结论:分数阶的阶数,即系统的记忆性,对粒子链的运动方向有显著影响.

4 结论

本文主要研究了粒子链在阶数和其他参数相互作用下的复杂输运现象.得到以下结论:1)系统的记忆性即系统的阶数对粒子链的运动状态有显著影响,在固定其他参数时,调节阶数将导致粒子链出现定向输运反向流,并在某一阶数产生随机共振;2)不同阶数的噪声-平均流速曲线v(D)表明,分数阶系统出现极大平均流速所需的噪声强度较之整数阶系统更小;并且在小噪声状态下,平均流速明显快于整数阶系统;3)当阶数固定时,耦合强度-平均流速曲线v(k)表明,平均流速会随耦合强度的变化出现广义共振,当阶数较大即系统记忆性较弱时,出现正向粒子流的广义共振,而当阶数较小即系统记忆性较强时,则出现反向粒子流的广义共振.

[1]H¨anggi P,Marchesoni F 2009 Rev.Mod.Phys.81 387

[2]Qian M,Wang Y,Zhang X J 2003 Chin.Phys.Lett.20 810

[3]Ai B Q,He Y F 2010 J.Chem.Phys.132 094504

[4]Wang H Y,Bao J D 2004 Physica A 337 13

[5]Csah´ok Z,Family F,Vicsek T 1997 Phys.Rev.E 55 5179

[6]Ai B Q,He Y F,Zhong WR 2011 Phys.Rev.E 83 051106

[7]Kumar K V,Ramaswamy S,Rao M 2008 Phys.Rev.E 77 020102

[8]Gehlen S V,Evstigneev M,Reimann P 2009 Phys.Rev.E 79 031114

[9]Fendrik A J,Romanelli L 2012 Phys.Rev.E 85 041149

[10]Zheng Z G 2004 Spatiotemporal Dynamics and Collective Behaviors in Coupled Nonlinear Systems(Beijing:Higher Education Press)p279(in Chinese)[郑志刚2004耦合非线性系统的时空动力学与合作行为(北京:高等教育出版社)第279页]

[11]Vadakkepatt A,Dong Y L,Lichter S,Martini A 2011 Phys.Rev.E 84 066311

[12]Nishikawa M,Takagi H,Shibata T,Iwane A H,Yanagida T 2008 Phys.Rev.Lett.101 128103

[13]Camp`as O,Kafri Y,Zeldovich K B,Casademunt J,Joanny J F 2006 Phys.Rev.Lett.97 038101

[14]Liu F,Anh V V,Turner I,Zhuang P 2003 J.Appl.Math.Comp.13 233

[15]de Andrade M F,Lenzi E K,Evangelista L R,Mendes R S,Malacarne L C 2005 Phys.Lett.A 347 160

[16]Braun O M,Kivshar Y S 2004 The Frenkel-Kontorova Model:Concepts,Methods and Application(New York:Springer)

[17]Han X Q,Jiang H,Shi Y R,Liu Y X,Sun J H,Chen J M,Duan W S 2011 Acta Phys.Sin.60 116801(in Chinese)[韩秀琴,姜虹,石玉仁,刘妍秀,孙建华,陈建敏,段文山2011物理学报60 116801]

[18]Bao J D 2009 Random Simulation Method of Classical and Quantum Dissipation System(Beijing:Science Press)p80(in Chinese)[包景东2009经典和量子耗散系统的随机模拟方法(北京:科学出版社)第80页]

[19]Oldham K B,Spanier J 1974 The Fractional Calculus(New York:Academic Press)

[20]Kou S C,Xie X S 2004 Phys.Rev.Lett.93 180603

[21]Gao S L,Zhong S C,Wei K,Ma H 2012 Acta Phys.Sin.61 100502(in Chinese)[高仕龙,钟苏川,韦鹍,马洪2012物理学报61 100502]

[22]Podlubny I 1999 Fractional Differential Equations(San Diegop,CA:Academic Press)

[23]Samko S G,Kilbas A A,Marichev O I 1993 Fractional Integrals and Derivatives Theory and Applications(New York:Gordon and Breach Science Publisher)