金属橡胶热物理性能理论与试验研究*

马艳红 仝小龙 朱彬 张大义† 洪杰

1)(北京航空航天大学能源与动力工程学院,北京 100191)

2)(中航商用发动机有限责任公司,上海 200241)

(2012年6月10日收到;2012年9月10日收到修改稿)

1 引言

金属橡胶材料是将金属丝卷成螺旋形,经过拉伸、编织、模压成型制得的弹性多孔材料,其密度小、比强度高,具有极好的力学性能、热机械性能、隔热性能、可塑性和环境适用性,广泛应用于机械设备中的高温、高压、腐蚀性介质及剧烈振动环境下的阻尼减振、热防护及降噪等领域[1−3].

目前大多数学者的研究都集中在金属橡胶的力学性能上,并取得了显著的成果,逐步形成了力学性能的设计技术[4−6];而热物理方面仅有极少的研究资料,且均为试验研究[7],尚未建立适用于分析其热物理性能的理论模型.金属橡胶热膨胀性能和热传导性能是衡量其长期工作在热循环载荷环境下的稳定性以及评价隔热效果的两大重要参数,因此开展对其热物理性能的研究,是将金属橡胶材料应用于恶劣环境下的热防护领域中不可缺少的基础理论工作.

金属橡胶一方面可看作是一种由金属丝和空气组成的两相多孔材料,另一方面其编织工艺又类似于编织型复合材料,其热物理热性与多孔材料和复合材料具有一定的相似性.由于多孔材料的热膨胀性能与组成材料自身的热学性能、内部结构形式以及刚度分布等密切相关,目前还没有建立较为完善的多孔材料热膨胀模型,多用试验来分析其热膨胀性能.编织型复合材料的热膨胀性能研究目前比较成熟,常用的混合定律[8]、Schapery模型[9]等在一定程度上都能较为准确地描述编织型复合材料的热膨胀性能.对材料热传导性能的研究大多以傅里叶定律为基础,采用热电比拟法[10]和有限元法[11,12]等,根据比等效相同法则从细观到宏观进行研究.

金属橡胶的热膨胀和热传导性能受金属丝螺旋卷的排列和孔隙分布的影响很大,而这两相的组成形式相当复杂,这给理论上研究金属橡胶的热膨胀行为和热传导性能带来一定的困难.本文以金属橡胶材料内部微元体结构为基础,利用热膨胀理论和热电比拟法,结合有限元法分析微元体结构的热膨胀和热传导性能.以金属橡胶内部微元体的接触状态为基础,分析不同接触状态下螺旋卷单元体的热物理关系,结合Schapery模型和比等效相同法则,从而建立金属橡胶材料的热膨胀和热传导分析模型,并结合相关热物理试验,为金属橡胶材料在热防护领域的应用提供了理论和试验基础.

2 金属橡胶微元体结构

金属橡胶加工成型后其内部由金属丝螺旋卷交错而成,金属丝螺旋卷的排列取向不规则.由于缠绕和编织等工艺,其内部将有两种最基本的排列形式:纵向和横向螺旋卷排列(如图1),两者为金属橡胶内部基本微元体结构[13],两种微元体不同排列构成了金属橡胶的基本单元.金属橡胶材料内部横向和纵向螺旋卷微元体之间包含空气,因此从热特性角度分析,金属丝卷和空气是组成金属橡胶的两种介质.因此针对微元体特殊的空间结构,合理地建立微元体热膨胀和热传导模型是分析金属橡胶材料宏观热性能的基础.下面将以建立微元体结构与热物理特性的关系方程为基础,建立细观结构和宏观性能之间的转换关系,从细观结构上阐明金属橡胶材料热物理性能的产生机理,进而建立相应的热物理模型.

图1 螺旋卷单元结构示意图 (d S为金属丝的丝径(mm);D L为螺旋卷的直径(mm);L J为螺旋卷的螺距(mm);α为螺旋卷轴线方向与载荷方向的夹角(rad))

3 金属橡胶的热膨胀性能研究

3.1 微元体结构热膨胀模型

首先采用有限元法对微元体结构的热膨胀行为进行分析,图2所示为在受热时纵向和横向微元体的热膨胀变形.由纵向和横向微元体热膨胀总变形可以看出,微元体受热后,螺旋结构形状不变,微元体的热变形变为在截面法向上被拉伸.由于微元体特殊的螺旋结构,内部的热膨胀力都垂直于螺旋卷的截面,热膨胀带来的热变形沿着螺旋卷旋向.因此纵向微元体热变形主要来自于轴向方向变形,横向微元体热变形主要来自于径向方向变形.

根据纵向和横向微元体的结构形式和热膨胀沿各方向变形的分布情况,可认为当微元体结构的温度变化∆T时,纵向微元体沿着轴向及横向微元体沿着径向的热变形为

图2 纵向和横向排列螺旋卷热膨胀总变形 (a)纵向;(b)径向

式中aS为金属丝材料的热膨胀系数(10−6°C−1).

因此根据热膨胀理论,纵向和横向微元体在螺旋轴向和径向的等效热膨胀系数为

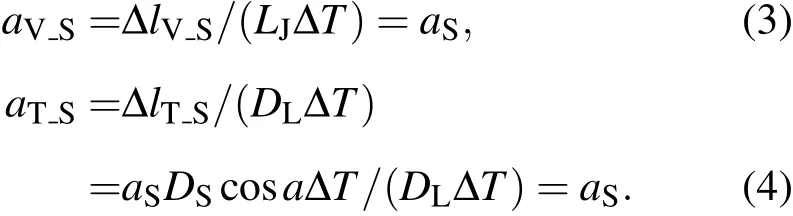
由(3)和(4)式,结合有限元的热膨胀变形分析,得到两种排列形式的微元体结构的热膨胀系数均与金属丝材料的相同,与螺旋卷的丝径、螺旋径、螺距以及排列形式无关.

3.2 基本单元的热膨胀模型

由上节的分析可知,如果将金属橡胶材料同样视为由螺旋卷构成的连续均匀框架结构材料,则可近似地认为金属橡胶的膨胀系数与金属丝材料相同[14],即aMR=aS.实际上纵向和横向微元体组成的基本单元相互接触构成了金属橡胶的宏观框架结构,因此分析孔隙对基本单元热膨胀性能的影响成为揭示金属橡胶热膨胀机理的重要基础.

基本单元在成型压力作用下存在三种接触状态:未接触、滑移接触和挤压接触[13].图3所示为加热后未接触和接触状态基本单元的热膨胀变形.对于未接触状态的基本单元,由于纵向和横向微元体之间轴向有间隙∆,下端横向螺旋卷的热变形首先要抵消其间的间隙,因此微元体间热变形相互不传递.对于接触状态的基本单元,此时两微元体间由于接触点的存在,横向微元体的热膨胀变形可以通过接触点的作用传递到纵向的微元体上,两者共同作用形成接触状态的热膨胀变形.

图3 未接触和接触状态基本单元的热膨胀变形 (a)未接触状态;(b)接触状态

根据对未接触和接触状态基本单元的结构形式和热膨胀的分析,结合微元体的热变形公式,可知未接触状态基本单元后热膨胀系数为

滑移接触和挤压接触两种接触状态基本单元的热膨胀系数为

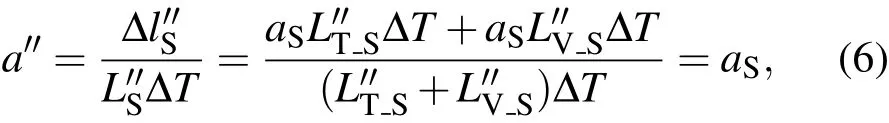
由上述热膨胀系数公式可以看出,由于间隙的存在,未接触状态基本单元热膨胀系数小于金属丝材料本身,即a′＜aS.对于接触状态基本单元,其热膨胀系数等同于金属丝材料本身.

可见,对于金属橡胶基本单元的热膨胀来说,在未接触状态基本单元轴向间隙的存在使得轴向热膨胀不能传递,导致金属橡胶宏观热膨胀性能下降;而当基本单元存在接触点时,接触状态基本单元间的孔隙将不影响其热膨胀性能.

3.3 金属橡胶材料的宏观热膨胀模型

对于常用的编织型复合材料而言,其宏观热膨胀性能不仅与各组分材料的热膨胀性能有关,还与各组分的弹性性能相关,Schapery模型[9]基于能量理论阐述了各组分之间热膨胀的相互影响.根据金属橡胶加工成型的方式可知,其由三种不同接触状态的螺旋卷基本单元按照一定的编织方式制作而成,类似于编织型复合材料.各接触状态单元体可看作为不同组分的材料,在不同相对密度下,在金属橡胶内部其各自的热膨胀性能、体积分数和弹性性能都不相同,对金属橡胶材料宏观热膨胀的贡献也不同.因此综合考虑几种接触状态之间的相互作用对金属橡胶热膨胀行为的影响,根据编织型复合材料热膨胀性能常用预测模型—–Schapery模型对金属橡胶的热膨胀性能进行预测,得到金属橡胶材料的热膨胀系数aMR为

式中Ei为三种不同接触状态基本单元的等效弹性模量,其中 E′≈ 2.56E′≈ 0.59E′′[13];ni为不同相对密度下三种不同接触状态基本单元的体积分数.

由对金属橡胶宏观热膨胀性能的分析可知,其不仅与不同接触状态基本单元自身的热膨胀性能有关,还与其体积分数和弹性模量有关.其中接触状态基本单元的热膨胀系数和各基本单元弹性模量不受金属橡胶材料参数的影响,而未接触状态基本单元的热膨胀系数和各基本单元的体积分数将直接受到相对密度的影响,这两个参数的变化规律将成为衡量金属橡胶热膨胀性能的主要因素.

3.4 金属橡胶热膨胀系数性能试验

试验研究采用DIL402PC型热膨胀仪对不同相对密度下的金属橡胶材料进行热膨胀性能测试,温度范围为 20°C—600°C,升温速率为 2°C/min,如图4所示.试验中采用高纯氩气进行气氛保护,利用计算机和智能仪表对温度和热变形量进行控制和测量记录.根据B4339-84标准计算金属橡胶的热膨胀系数[15].

图4 试验仪器402-PC和热膨胀试验样件

金属橡胶材料采用圆柱体结构,金属丝材料为GH4169,直径为9.6 mm,高度为34—37 mm,具体样件的材料参数见表1.

表1 金属橡胶热膨胀试验样件参数

图5为不同相对密度下热膨胀系数随温度变化的曲线.不同相对密度下的金属橡胶热膨胀系数都随温度的升高而变大,但都比原金属丝材料的热膨胀系数小;并随着相对密度的增加热膨胀系数逐步变大,最后越来越接近金属丝材料本身的热膨胀系数.当温度在100°C到大约300—400°C之间范围内时,金属橡胶热膨胀系数值随温度的升高急剧增加,并且为金属丝材料热膨胀系数的0.5—0.7.当温度在300—400°C以上,金属橡胶的热膨胀系数随温度升高的增大趋于平缓,并且为金属丝材料热膨胀系数的0.85—0.9.

图5 不同相对密度下金属橡胶热膨胀系数与温度的关系

温度较低时,金属橡胶内部主要以未接触状态的基本单元为主,即未接触状态的基本单元的体积分数较大.根据(5)和(7)式,未接触状态基本单元的热膨胀性能对金属橡胶宏观热膨胀性能的影响起主要作用,因此温度较低时明显阻碍了金属橡胶的热膨胀.当温度逐渐升高时,微元体自身热膨胀的变形开始逐步增加,热变形填充了未接触螺旋卷之间的孔隙,即未接触的螺旋卷开始转换为接触状态[10],接触状态的体积分数开始增多.根据(6)和(7)式,未接触状态基本单元之间的间隙对宏观热膨胀变形的阻碍能力有限,金属橡胶热膨胀的变化趋势开始和金属丝材料一致,越来越接近金属丝材料本身的热膨胀系数.随着相对密度的增加,内部未接触的基本单元的体积分数越来越少[10],其对金属橡胶材料的热膨胀抑制作用也降低,因此热膨胀系数增大.

4 金属橡胶材料的导热性能研究

4.1 金属橡胶的传热过程

金属橡胶多孔介质中含有气体和金属丝,其内部的传热途径主要有以下三种模式:相互接触的金属丝及空隙中气体的导热;空隙中气体的对流换热;金属丝或气体之间的辐射换热,如图6所示.

大量试验研究和理论分析结果表明,当多孔介质中含湿量较低时,且内部孔隙中流体处于静止状态或流动甚微时,空隙中流体的对流换热贡献可忽略不计[16].而辐射换热贡献只是在温度较高、且空隙为真空或由气体占据时才比较明显[17].鉴于金属橡胶材料的传热过程非常复杂,为便于传热方程的联立及求解,可把金属橡胶的传热过程考虑成纯导热过程.对于金属橡胶多孔材料的纯导热过程,一般包括:金属丝的导热过程;金属橡胶中空气和金属丝与空气之间的导热过程;金属丝之间存在接触热阻时的导热过程.

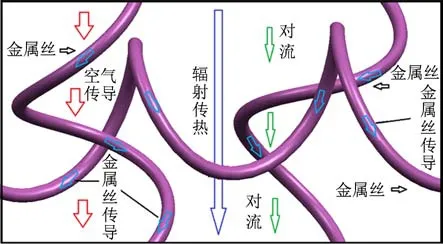
图6 金属橡胶材料内部传热过程

金属橡胶内部导热过程非常复杂,很难求得导热问题的解析解,因此有必要从内部微元体热导过程入手研究,建立导热单元体.每个导热单元体都是一个含有导热金属丝的立方体,根据比等效导热系数法则,金属橡胶材料的有效导热系数近似等于单元体的导热系数.

4.2 微元体结构导热模型

金属橡胶是一种多孔材料,内部由金属丝螺旋卷交错而成,并且金属丝螺旋卷始终贯穿于整个金属橡胶之中,形成了各个方向的导热网链.当金属橡胶的成型方向为热流方向时,纵向微元体排列形式为螺旋卷的轴向方向与热流方向平行,横向微元体排列形式则为轴向方向与热流方向垂直.

图7(a)所示为采用有限元法[11]得到的纵向微元体和螺旋卷的热流分布图.由于螺旋卷微元体的特殊的螺旋上升卷结构,热流进入纵向和横向螺旋卷微元体后,与加载热流方向成一定的角度,主要通道为沿着纵向螺旋卷中心线的切平面.

由此分析得到纵向微元体传导形式和热阻模型如图7(b),(c)所示.根据傅里叶定律,纵向排列的螺旋卷等效热阻为R1Vh,其为一根与热流方向成一定角度的金属丝的等效热阻,因此通过纵向排列螺旋卷的热流为

因此其在热流方向的等效热阻为

横向排列螺旋卷中热流的主要通道为两个相互并联的1/2横向微元体,与加载的热流方向成一定角度,如图8所示.由此分析得到的纵向微元体的传导形式和热阻模型如图8(b),(c)所示.根据(8)式,其在热流方向的等效热阻为

图7 纵向排列微元体的热传导形式和热阻模型 (a)热流分布;(b)传导形式;(c)热阻模型

图8 横向排列微元体的热传导形式和热阻模型 (a)热流分布;(b)传导形式;(c)热阻模型

4.3 基本单元的导热模型

对于金属橡胶的导热过程而言,不同接触状态下的微元体力学性能和热膨胀性能不同,但是微元体之间具有相互串联和并联的关系,可以传递热量,因此接触状态的不同并不影响热量的传递.因此分析金属橡胶的热传导过程时,可以把单位体积内一定数量的螺旋卷看作为均匀的金属橡胶导热单元体,金属橡胶考虑为由一系列导热单元体(立方体)连接而成.由金属橡胶毛坯的编织和模压成型工艺可知,成型方向上毛坯的高度为成型后高度的r倍.金属橡胶导热单元体内具有2r个螺旋卷,r个纵向排列微元体为串联结构,而r个横向排列微元体表现为并联结构,见图9.

因此在长度为DL的单位立方体内,根据(9)式可得导热单元体内串联后的纵向螺旋卷在热流方向的等效热阻[10]为

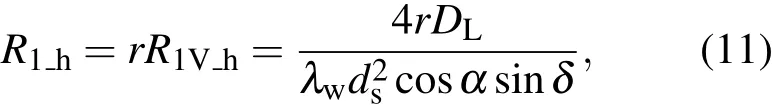
式中δ=arctan(LJ/r/πD).

根据(10)式微元体内纵向螺旋卷串联结构在热流方向的等效热阻为

空气的等效热阻为

λa为空气的导热系数.

根据三部分热阻的并联关系,金属橡胶导热单元体在热流方向上总等效热阻为

因此单元体等效导热系数λh为

图9 单元体热传结构示意图和热阻模型

4.4 金属橡胶材料导热模型

金属橡胶螺旋卷的数量为在一定相对密度下在图9中所示排列基础上,按照成型方式成比例均匀地增加得到的螺旋卷数目,单位螺旋卷体积内,相对密度与金属橡胶螺旋卷的几何参数的关系可表示为

式中:ρMR为单位体积内金属橡胶的密度,ρS为金属丝的密度,N为一定相对密度下螺旋卷微元体的数目.

一定相对密度的金属橡胶模压成型后,在单位体积内由N/2r个微元体并联而成.因此根据(15)和(16)式,金属橡胶等效导热系数λMR公式可表示为如下形式:

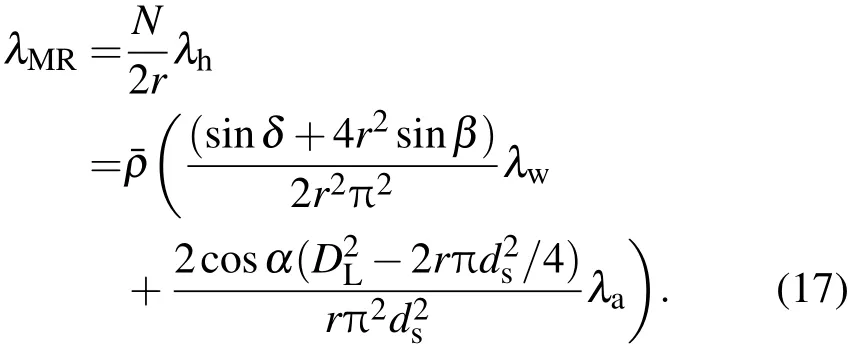
由(17)式可知,金属橡胶的导热系数由金属螺旋丝和空气的热导系数组合而成,其相互所占的比例与金属橡胶的细观结构和工艺参数有关,即与相对密度、螺旋丝卷直径及金属丝材料参数有关.在金属橡胶内部螺旋卷微元体结构形式不变的情况下,金属橡胶的导热系数与相对密度和金属丝材料的导热系数成一次线性关系,微元体结构参数将影响此线性关系的比例系数.金属丝材料本身的导热系数决定了金属橡胶导热系数的大致范围;相对密度和微元体结构参数的影响使得导热系数在这一范围区间内变化.

4.5 金属橡胶导热性能

采用了LFA427激光热导测试仪测试不同相对密度的金属橡胶材料的导热系数随温度的变化规律,试验仪器和试验件见图10,金属丝材料均为GH4169,厚度1.5 mm,直径12.7 mm,样件参数见表2.

表2 金属橡胶导热系数试验件各项参数

图11所示为不同温度下采用理论模型分析以及试验测试得到的金属橡胶导热系数和金属丝材料本身导热系数的对比,采用C-4试验件.试验结果与理论模型结果都表明金属橡胶导热系数随着温度的升高成比例地增大.不同温度下的试验测量值稍小于理论分析值,误差为15%以内.

图10 LFA427试验仪器和金属橡胶样件

图11 金属橡胶导热系数随温度的变化

由金属橡胶的受压力学性能和导热性能分析可知,随着温度的升高,金属橡胶内部的螺旋卷接触状态发生变化,但是从理论公式(17)和试验结果来看,金属橡胶导热系数的增大和金属丝材料的导热系数成正比,说明温度升高导致接触状态的变化并不影响螺旋卷热传导过程,证明了模型中金属橡胶材料内部导热单元均匀的热传导假设的正确性.

图12所示为当温度低于80°C时,采用理论模型分析和试验测量结果得到的金属橡胶导热系数随相对密度的变化规律.理论和试验结果均表明金属橡胶的等效导热系数随相对密度的增加近似成线性增大,在此相对密度范围内误差小于20%,相对于评定金属橡胶导热性能和金属丝材料的导热系数相比影响可以忽略.结合金属橡胶导热系数随温度和相对密度的变化规律,可得相对密度在0.1—0.25区间内,金属橡胶等效导热系数相当于金属丝材料的1%—3%.

相对密度增加时,金属丝材料质量增加,更多金属丝参与导热,由于金属丝导热系数远大于空气,因此根据(17)式金属橡胶导热系数近似线性增加.另一方面热量自外传入金属橡胶进行热传导,当遇到金属丝时,其导热系数大,大部分热量通过金属丝传递,而小部分热量则绕过金属丝通过孔隙传递.由于内部金属丝含量较低,且螺旋卷结构传热的路径相对较长和复杂,导致金属橡胶材料的导热性能下降,根据(17)式

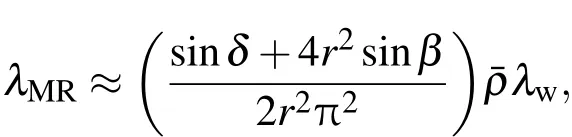
微元体特殊的结构参数和工艺参数导致金属橡胶的导热系数远小于丝材的热导系数与相对密度的乘积,即λMR≪¯ρλS.

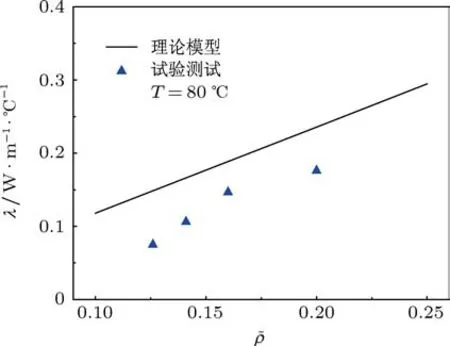
图12 金属橡胶导热系数随相对密度的变化

5 结论

本文针对恶劣环境下金属橡胶热防护构件的设计和热稳定问题,基于螺旋卷微元体结构,提出并建立了金属橡胶的热膨胀模型和热传导模型,并进行了试验验证,为金属橡胶材料在高温环境下的应用及其在热防护方面的设计提供了理论基础.得到以下结论.

1)金属橡胶的宏观热膨胀行为主要由相互接触的螺旋卷单元体的细观热膨胀变形产生.未接触状态微元体间的间隙和接触状态间的相互转换,是金属橡胶热膨胀系数较低和随相对密度变化的本质原因.金属橡胶内部的孔隙只在温度(小于大约300—400°C)较低时,对热膨胀起到一定的阻碍作用.

2)金属橡胶的导热系数由金属丝和空气的导热系数组合而成,二者的组成比例与微元体的细观结构和金属橡胶的工艺参数有关.较低的相对密度使得金属橡胶内部的金属丝含量低;微元体特殊的螺旋结构使得其导热路径较长和复杂,从而使金属橡胶导热性能下降.金属橡胶导热系数为金属丝材料本身的1%—3%.

3)理论与试验结果均证明了金属橡胶材料热膨胀系数低于金属丝材料本身,并具有较低的导热系数,可作为一种良好的热防护材料.本文的理论和试验研究为金属橡胶构件在高温、恶劣工程领域的阻尼/隔热防护设计的应用奠定了理论基础和试验依据.

[1]Al K 2002 Ph.D.Dissertation(TX:Texas A&M University)

[2]Ma Y H,Hong J,Zhang D Y,Wang H 2007 Proceedings of ASME TURBO EXPO Montreal,Canada,May 14–17,2007 p27585

[3]Ma Y H,Wang H,Li H Y,Hong J 2008 Proceedings of ASME TURBO EXPO Berlin,Germany,June 9–13,2008 p50961

[4]Ma Y H 2005 Ph.D.Dissertation(Beijing:Beihang University)(in Chinese)[马艳红2005博士学位论文(北京:北京航空航天大学)]

[5]Bugra E,Luo H,Darren H 2009 Proceedings of the 17th American Institute of Aeronautics and Astronautics Palm Springs,California,May 4–7,2009 p2521

[6]Yan H,Jiang H Y,Liu W J,Hao Z D,Ulannov A M 2010 Acta Phys.Sin.59 4065(in Chinese)[闫辉,姜洪源,刘文剑,郝振东,Ulannov A M 2010物理学报59 4065]

[7]Chegodayev D E(Translated by Li Z Y)(Russia)2000 The Designing of Components Made of Metal Rubber(Beijing:Publishing Company of National Defence Industry)p42(in Chinese)[契戈达耶夫D E著(李中郢译)2000金属橡胶构件的设计(北京:国防工业出版社)第42页]

[8]Fei WD,Wang L D 2004 Mater.Chem.Phys.85 450

[9]Schapery R A 1968 J.Compos.Mater.2 380

[10]Kim D K 2008 Ph.D.Dissertation(TX:Texas A&M University)

[11]Li W Z,Wang J 2012 Acta Phys.Sin.61 114404(in Chinese)[黎威志,王军2012物理学报61 114401]

[12]Sanada K,Tada Y,Shindo Y 2009 Composites A:Appl.Sci.Manufact.40 724

[13]Zhu B,Ma Y H,Zhang D Y,Hong J 2012 Acta Phys.Sin.61 078101(in Chinese)[朱彬,马艳红,张大义,洪杰2012物理学报61 078101]

[14]L¨u Y F 2006 Ph.D.Dissertation(Hefei:Hefei University of Technology)(in Chinese)[吕艳凤2006博士学位论文(合肥:合肥工业大学)]

[15]Jing Q,Liu R P,Shao G J,Wang W K 2004 Acta Phys.Sin.53 1440(in Chinese)[景勤,刘日平,邵光杰,王文魁2004物理学报53 1440]

[16]Farouki O T 1981 Thermal Properties of Soils(Hanover:U.S.Army Cold Regions Research and Engineering Laboratory)

[17]Aduda B O 1996 J.Mater.Sci.31 6441