用广义变分迭代理论求一类相对转动动力学方程的解*

石兰芳 莫嘉琪

1)(南京信息工程大学数学与统计学院,南京 210044)

2)(安徽师范大学数学系,芜湖 241000)

(2012年9月6日收到;2012年9月21日收到修改稿)

1 引言

近年来,转动相对Birkhoff系统动力学理论有了一些新的发展[1,2].例如文献[3,4]利用相对性原理,建立了弹性转轴任意两个横截面间的相对转动的动力学模型.相对转动非线性动力系统是具有复杂的动力学行为.文献[5]研究了一类相对转动非线性动力学系统的混沌运动表现.文献[6]针对一类非线性阻尼和强迫周期力项的相对转动非线性动力学系统,并用Yoshizawa非线性系统周期解的理论,证明了系统解存在惟一性和有界性,得到了自治系统存在极限环及稳定性的条件,并研究了其精确解.

非线性问题是数学物理界十分重视的一个问题[7].近年来,许多学者做了大量的工作[8−10],许多近似方法被发展,包括匹配法、合成展开法、边界层法、多重尺度法等.文献[11—21]利用渐近理论研究了一类非线性问题.本文讨论一类相对转动非线性扰动动力学的模型,利用变分原理,构造了广义变分迭代式来求出任意次精度的近似解.

2 相对转动系统动力学模型

考虑如下一类弹性转轴任意两端间的相对转动系统的非线性扰动动力学模型[5,6]:

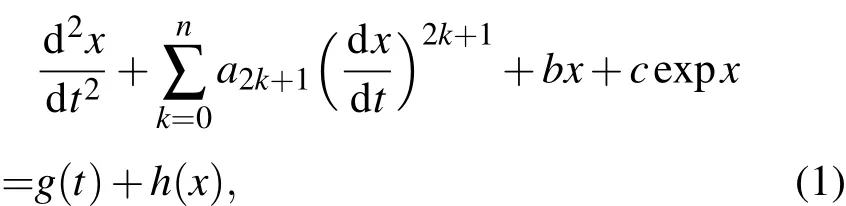
其中x=θ2−θ1为相对转角,θ1θ2分别为弹性转轴两端面的转角;g(t)=(T2−T1),J为弹性转轴的转动惯量,T1,T2分别为弹性转轴两端面的外加力矩,常数 b ＞ 0,c≥ 0,a1＞ 0,a2k+1≥ 0(k=1,2···,n),且h(x)为非线性强迫扰动函数,设它是充分光滑的有界函数.

3 广义变分迭代

为了进一步求得相对转动系统的非线性动力学扰动方程(1)式的近似解,引入泛函

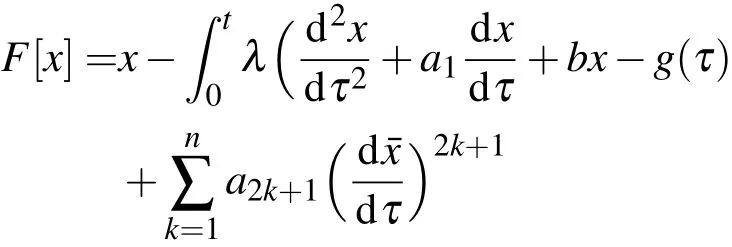
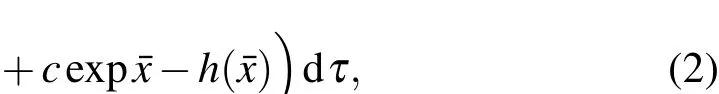
令δF=0,于是有

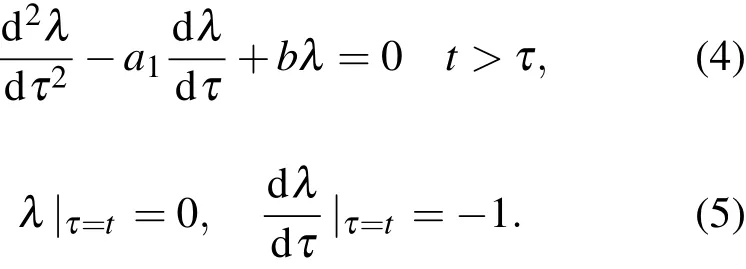
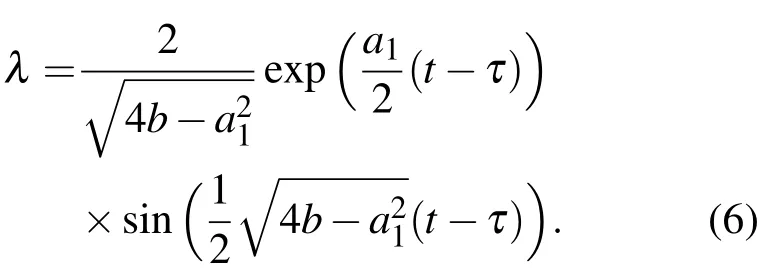
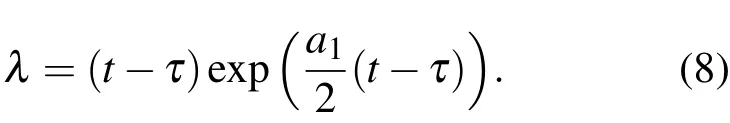
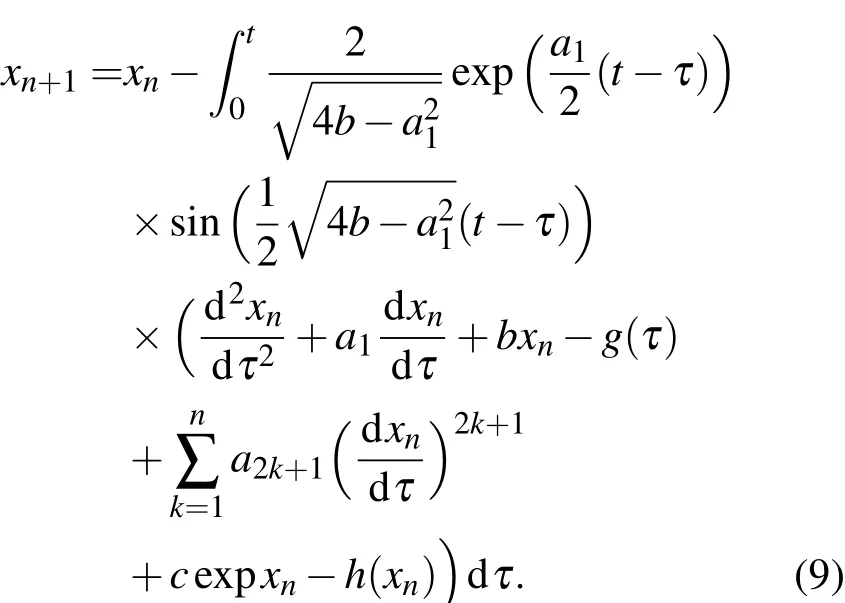
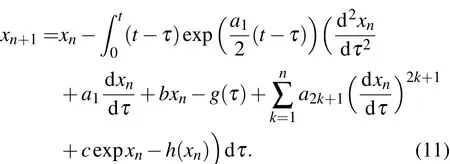
由迭代式(9),(10),(11)式,当分别选定零次近似函数x0后,可以分别逐次求出方程(1)的n次渐近解xn(n=1,2,···).又由于相对转动系统的非线性动力学扰动方程(1)式的结构及扰动项的解析性和不动点原理[23],就是原方程(1)式的解.

因为迭代式(9),(10),(11)式出自于不同的三个Lagrange乘子,因而得到的迭代近似解性态也不同,这说明在对应的系数a＜4b,a＞4b,a=4b情形下,原相对转动系统的非线性扰动动力学方程(1)有三种不同性态的解.

4 相对转动系统的一个相关物理特例

为了便于比较,现考虑一个简单的微扰相对转动系统的非线性动力学模型.设方程(1)中的规范化无量纲参数a0=2,a1=ε,n=1,b=2,c=0.并且设g(t)=sin t,h(x)=εcos x,其中ε为正的小参数0＜ε≪1.这时相对转动系统的非线性动力学方程为

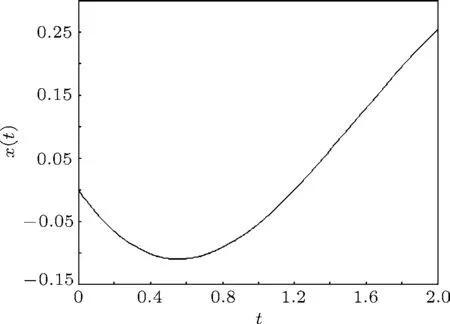
图1 方程(12)精确解x(t)的模拟曲线,ε=0.1,x(0)=0,x(0)=−

为了能更好地得到近似度较高的近似解,下面来选取零次迭代x0(t).考虑对应于模型(12)的线性方程

方程(14)的解为

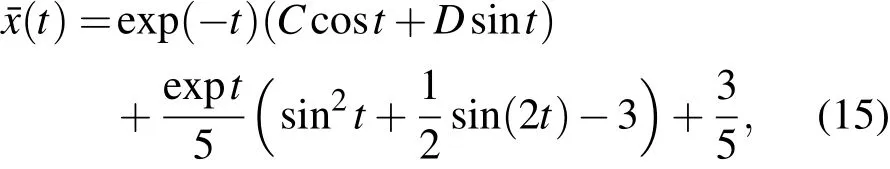
选取相对转动系统的非线性动力学方程(12)的零次近似函数x0(t)为(15)式决定的x¯(t).即

由零次近似函数(16)式及迭代关系式(13)式,可得非线性动力学方程(12)的一次近似解x1(t):

由(17)式和迭代关系式(13)式可得非线性动力学方程(12)的二次近似解x2(t):

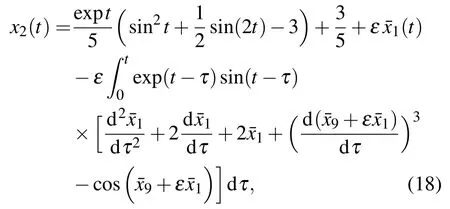
其中

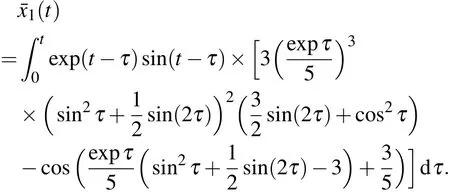
作为比较,当选取ε=0.1时,用数值模拟方法求得模型(12)式的精确解x(t)和用广义迭代方法求出的二次近似数值解x2(t)参见表1.由表1可以看出两者之间很接近.

继续用迭代关系(13)式可依次得到非线性动力学方程 (12)的 n 次近似解 xn(t)(n=3,4,···),显然,用广义迭代方法求出的更高次的近似解与模型(12)的精确解更加接近.

表1 方程(12)模拟数值精确解x(t)与二次迭代模拟数值解x2(t)比较

5 与扰动解的精度比较

由于相对转动系统的非线性动力学方程(12)为扰动方程,故我们还可用摄动方法求其渐近解.设(12)式的渐近解t,ε)为

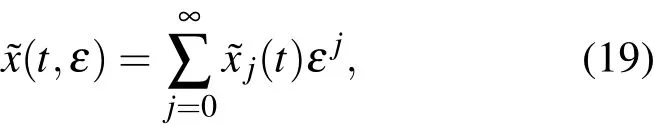
将(19)式代入方程(12),按ε的幂展开非线性项,合并ε的同次幂项,并令各次幂的系数为零.由ε0的系数为零,得

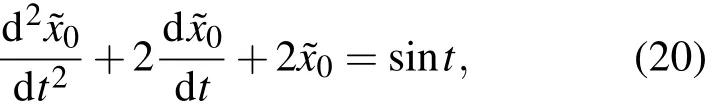
方程(20)的解为(仍然设任意常数为零)

将(19)式代入方程(12),由ε1的系数为零,得

方程(22)的解为

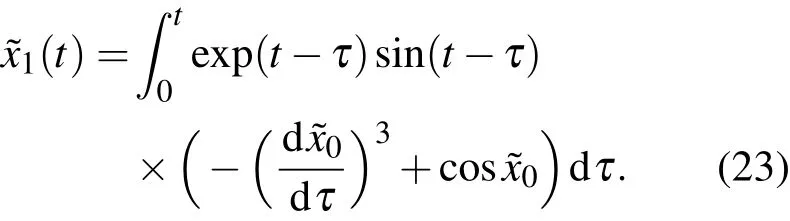
将(21)式代入(23)式,可得

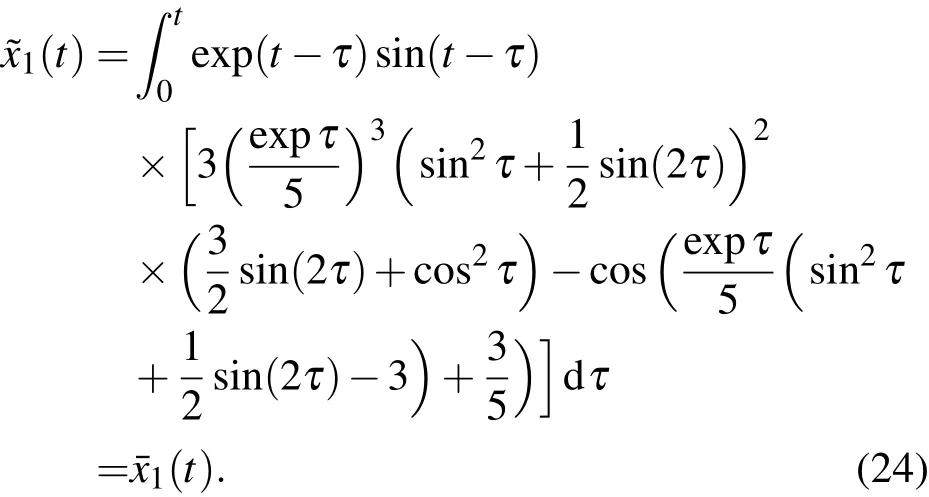
将(19)式代入方程(12),由ε2的系数为零,得

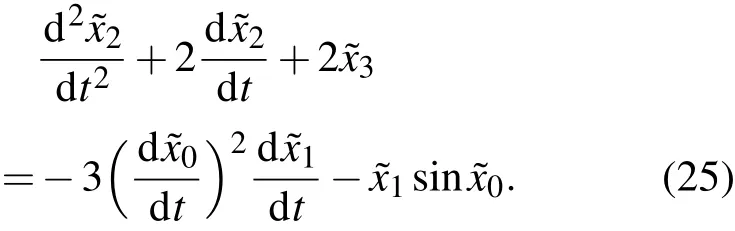
方程(25)的解为

将(21),(24)式代入上式,可得

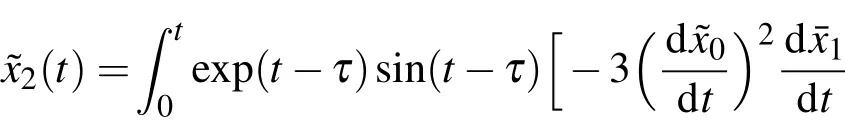
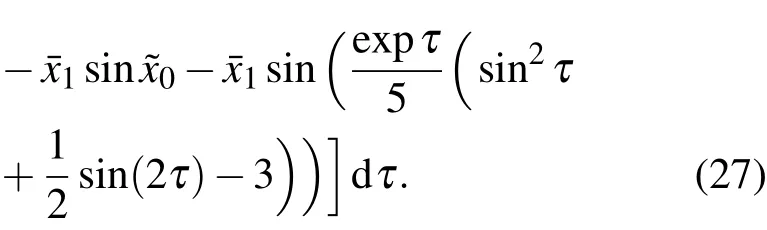
于是,由(19),(21),(24),(27)式,相对转动系统的非线性动力学扰动方程(12)的二次摄动渐近解2per(t)为

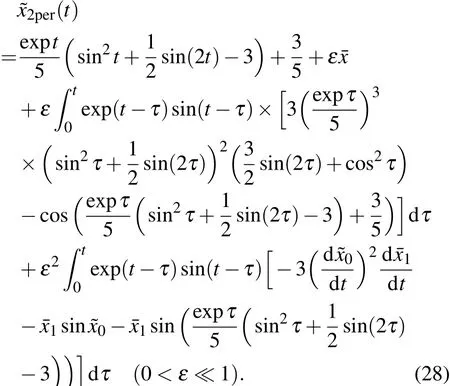
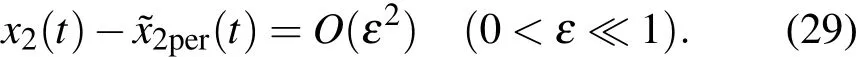
由此可知,对于相对转动系统的非线性动力学方程(12),利用广义变分迭代方法求出的近似解和用摄动方法求出的渐近解具有相同的近似度.

利用广义变分迭代方法在一定的情况下可以求解诸如相对转动系统的一类非线性动力学模型.它不一定必须要在方程中含有小参数.所以在一定的场合下用此方法也能得到非摄动方程的近似解.

6 讨论

广义变分迭代方法是利用变分原理,引入Lagrange乘子,再应用变分的极值条件选定合适的Lagrange乘子.这样依次得到的各次迭代解具有较快的近似度.

广义变分迭代方法,对初始迭代的选取十分关键.选取合理,能较快地得到所要求精度的近似解.一般总是选取原非线性方程对应的线性部分所构成的线性方程的解作为原方程的初始迭代.当然,也可根据原方程的特点或模型的物理性态来选取初始迭代,这样可以快捷地得到所要求精度的近似解.

7 结论

用广义变分迭代方法求解相对转动的非线性动力学模型的近似解是一个简单而有效的方法.用广义变分迭代方法得到的近似解不是简单的离散数值解,它还可继续进行解析运算,并可做相应的定性和定量方面的分析.同时,本文选取初始近似u0(t),是线性情形下典型系统的解.它保证了相对转动非线性动力学模型(1)式较快地求得在所求的精度范围内的近似解.

[1]Fu JL,Chen L Q,Xue Y 2003 Acta Phys.Sin.52 256(in Chinese)[傅景礼,陈立群,薛纭2003物理学报52 256]

[2]Wang K 2005 Acta Phys.Sin.54 5530(in Chinese)[王坤2005物理学报54 5530]

(4)创新驱动效应偏低，自主研发能力有待加强。湖北省汽车零部件产业集聚了很多仅有组装生产功能而无研发能力的零部件企业，但技术研发能力强、营业规模超10亿元级的龙头企业还很少。另外，还缺乏汽车零部件方面的公共创新服务平台，导致整体创新驱动效应明显不足，汽车零部件技术研发、检验检测、产业孵化等公共配套服务缺乏，无法有效促进整体汽车零部件技术和生产工艺的提升。

[3]Zhao W,Liu B,Shi P M,Jiang J S 2006 Acta Phys.Sin.55 3852(in Chinese)[赵武,刘彬,时培明,蒋金水2006物理学报55 3852]

[4]Shi P M,Liu B 2007 Acta Phys.Sin.56 3678(in Chinese)[时培明,刘彬2007物理学报56 3678]

[5]Shi P M,Liu B,Hou D X 2008 Acta Phys.Sin.57 1321(in Chinese)[时培明,刘彬,侯东晓2008物理学报57 1321]

[6]Wang K,Guan X P,Qiao J M 2010 Acta Phys.Sin.59 3648(in Chinese)[王坤,关新平,乔杰敏2010物理学报59 3648]

[7]Barbu L,Morosanu G 2007 Singularly Perturbed Boundary-Value Problems(Basel:Birkhauserm Verlag AG)

[8]Barbu L,Cosma E 2009 J.Math.Anal.Appl.351 392

[9]Ramos M 2009 J.Math.Anal.Appl.352 246

[10]Sagon G 2008 Nonlinearity 21 1183

[11]Mo J Q 2009 Sci.China G 52 1007

[12]Mo J Q 2009 Chin.Phys.Lett.26 010204

[13]Mo J Q 2010 Commun.Theor.Phys.53 440

[14]Mo J Q 2010 Chin.Phys.B 19 010203

[15]Mo J Q,Lin Y H,Lin W T 2010 Chin.Phys.B 19 030202

[16]Shi L F,Zhou X C 2010 Acta Phys.Sin.59 2915(in Chinese)[石兰芳,周先春2010物理学报 59 2915]

[17]Shi L F,Mo J Q 2010 Chin.Phys.B 19 050203

[18]Shi L F,Chen C S,Zhou X C 2011 Chin.Phys.B 20 100507

[19]Shi L F,Zhou X C,Mo J Q 2011 Acta Phys.Sin.B 60 110205(in Chinese)[石兰芳,周先春,莫嘉琪2011物理学报60 110205]

[20]Shi L F,Ouyang C,Mo J Q 2012 Acta Phys.Sin.61 120201(in Chinese)[石兰芳,欧阳成,莫嘉琪2012物理学报 61 120201]

[21]Shi L F,Ouyang C,Chen L H,Mo J Q 2012 Acta Phys.Sin.61 050203(in Chinese)[石兰芳,欧阳成,陈丽华,莫嘉琪2012物理学报61 050203]

[22]He J H 2002 Aproximate Nonlinear Analytical Methods in Engineering and Sciences(Zhengzhou:Henan Science and Technology Press)(in Chinese)[何吉欢2002工程与科学计算中的近似非线性分析方法(郑州:河南科学技术出版社)]

[23]de Jager E M,Jiang F R 1996 The Theory of Singular Perturbation(Amsterdam:North-Holland Publishing Co.)