基于支持向量机的中小上市公司财务评价模型构建

高爱霞，周英洪

(1.山东财经大学 东方学院，山东泰安 271000;2.山东省交通干部学校培训科，山东济南 250031)

一、引 言

财务评价是公司财务管理的重要环节［1］。科学有效地对公司的财务状况进行评价，不仅对公司财务危机预防有很重要的作用，对于促进资本市场更好更快发展也至关重要。因此，对公司财务状况的评价研究一直是学术研究的热点。传统的公司财务状况评价方法有单变量模型、Z-SCOR多元判别模型、AZETA模型、Y分数模型、ARCH自回归异方差模型、ARMA自回归滑动平均模型、线性判定分析、多元线性回归分析、灰色关联预测及马尔科夫琏等预测模型。阎娟娟等人［2］、李云飞等人［1］都指出，财务状况评价从本质上来讲是一个非线性问题，而这些传统的评价方法多是直接或间接依赖于线性函数来建立模型，往往不能拟和复杂的实际财务数据。相比传统的研究方法，人工智能方法在处理非线性复杂问题时，克服了传统模型依赖线性函数建立模型的缺陷，提高了模型的精度，其中应用最为广泛的是人工神经网络方法，如吴德胜等人［3］、杨淑娥等人［4］、Pendharkar［5］、Back 等人［6］、Yang 等人［7］、Zhang 等人［8］都各自采用不同的人工神经网络模型对企业的财务状况进行评价，并与传统的线性模型方法得出的结果进行了对比，证明人工神经网络方法在精度上优于传统的线性方法。

但是，沈明华等人［9］发现，传统人工神经网络方法在财务分析应用中也是有缺陷的，存在网络结构难于确定、过学习或欠学习以及局部极小等问题。李云飞等人［1］将人工神经网络方法的缺陷归纳为:结构设计没有固定的模式，缺乏严格理论依据的设计程序;要求训练样本足够多;只能保证对有限个样本的误差达到极小，网络推广能力较差;学习训练过程常常陷入局部极小点，无法保证训练效果等。

近年来，伴随着智能算法的发展，将支持向量机(Support Vector Machine，缩写为SVM)引入企业财务评价模型中受到学术界的关注。李云飞等人［1］认为支持向量机能够克服人工神经网络方法的诸多缺陷，将实际问题通过高维空间转化，在高维的特征空间利用线性分类完成低维空间中的非线性分类任务，解决了维数灾难，并具有很好的推广能力，提高了运算速度。阎娟娟等人［1］采用SVM构建的财务评价模型对2001年至2004年280家上市公司(其中包括140家ST公司)的财务报表数据进行实证分析，并与反向传播(Back Propagation，缩写为BP)神经网络方法进行了比较，结果表明在分类能力和预测能力上，SVM模型的精度都高于BP神经网络方法。周晓斌等人［10］采用主成分分析和支持向量机理论相结合的方法对沪深两市2003至2005年60家上市公司的财务状况进行了评价，获得了较满意的结果，提出可以用支持向量机评价上市公司的财务状况。李云飞等人［1］采用遗传算法+支持向量机(GA-SVM)方法建立上市公司财务评价模型，并运用该模型对沪深两市2007年至2009年度120家A股上市公司的财务状况进行了评价，结果验证了该模型的有效性。何晓庆等人［11］则是结合主成分分析法和支持向量机构建评价模型，对我国2003年至2004年140家A股上市公司的财务状况进行了评价，结果也表明基于支持向量机的财务评价模型在推广能力方面同样有着较为理想的精度。

支持向量机(SVM)是Cortes和Vapnik于1995年在VC维理论和结构风险最小原理基础上提出的一种机器学习方法，它在解决有限样本、高维模式识别、非线性等复杂问题中表现出许多特有的优势，目前SVM已被成功应用于识别、回归、分类问题中。安欣等［12］的研究指出，SVM在实现结构风险最小化的基础上成为解决回归分析和模式分类问题的有效工具。其中，处理回归分析问题的支持向量机称为支持向量回归机(Support Vector Regression，缩写为SVR)，处理模式分类的支持向量机称为支持向量分类机(Support Vector Classification，缩写为SVC)。SVM解决分类问题的时候，样本的维数是无关变量，这使得SVM很适合解决分类问题。当然，SVM具有这样能力也因为引入了核函数，用核函数绕过维度变换，直接用低维度的参数带入核函数来等价计算高维度向量的内积。核函数的基本作用就是接受两个低维空间里的向量，计算出经过某个变换后在高维空间里的向量内积值，从而实现算法的非线性化。SVC的核心思想是利用内积核函数代替一个非线性映射，把数据样本从原空间映射到一个高维特征空间，并在该空间中线性可分，然后再在这个高维空间中求最优分类面来实现理想的分类结果。

本研究选取我国2009年276家中小上市公司作为研究样本，样本公司财务数据易得、完整，具有可比性，其中有两家公司是被深交所披露为财务异常的公司，即ST(Special treatment)公司;其余为正常公司。根据支持向量机的原理和方法建立评价模型，对276家中小上市公司的财务状况进行分类。再根据分类的结果验证该评价模型能否精确地分类财务状况优劣的公司。为此，首先建立财务指标评价体系，选取能够决定和反映公司获利能力、营运能力、偿债能力、发展能力四个方面的10个传统财务指标，对276家中小上市公司的整体发展质量进行比较;然后以这276家公司的财务数据作为输入特征向量，采用支持向量机方法构建公司财务评价模型;最后对中小上市公司的财务评价模型进行检验，以验证该评价模型的有效性。

二、财务指标的选取

财务状况不仅关系着公司的正常运转，也是公司形成有效竞争力的必要条件［13］，它主要体现在获利能力、营运能力、偿债能力、发展能力等四个方面，是一个综合评价的结果。而公司的财务评价结果，可以为公司决策人员和利益相关人员提供重要的决策依据［14］。上市公司财务评价是一个包含多个指标的评价系统，包含能体现企业发展的多个方面的数据［10］。选取准确的财务指标是公司财务评价的重点和难点之一，更是目前公司财务评价研究的热点。参考一些学者的研究［14-17］，本文选取能够反映获利能力、营运能力、偿债能力、发展能力四个方面的10个传统财务指标，对276家中小上市公司的财务状况进行评价。获利能力是公司能否生存与发展的前提，在财务管理中一般可以通过“净资产收益率”和“总资产报酬率”等指标来反映这种能力的大小，同时，考虑到现金状况对公司财务预警有着特殊意义，本文提出用“盈余现金保障倍数”予以补充，以更好地克服传统利润指标的缺陷;营运能力是公司运用各项资产以赚取利润的能力，其好坏直接关系到公司资金的周转快慢，财务管理中一般采用“流动资产周转率”和“总资产周转率”等指标予以分析;公司偿债能力通常采用“资产负债率”和“利息保障倍数”来衡量，同时可以采用“现金流动负债比率”反映公司的偿债能力的质量，公司如果没有足够的偿债能力，将会面临破产危机;发展能力是公司生存下去的源动力，可采用“销售增长率”、“资本积累率”指标反映企业销售变动趋势和资本扩张情况来衡量。

我们所选取的上述中小上市公司财务指标的计算公式及2009年276家中小上市公司的实际财务指标分别见表1和表2。

表1 财务指标计算公式

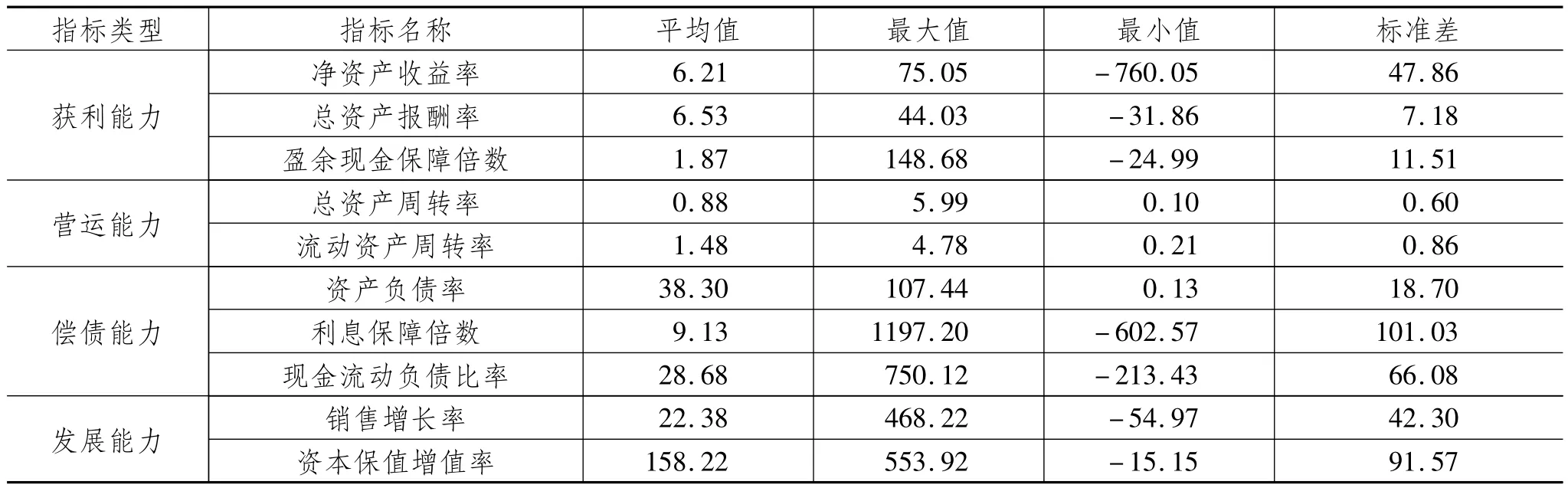
表2 2009年度我国中小上市公司财务指标一览表

由表2可以看出，我国中小上市公司在整体发展质量上存在较大差异，除营运能力的两个指标，即总资产周转率和流动资产周转率变化范围不大外(其标准差分别为0.60和0.86)，其他如净资产收益率、盈余现金保障倍数、资产负债率、利息保障倍数、现金流动负债比率、销售增长率、资本保值增值率等指标的变化范围都很宽，最大者为利息保障倍数，标准差达到101.03，资本保值增值率标准差达91.75，现金流动负债比率标准差达66.08，净资产收益率标准差达47.86，销售增长率标准差达42.30。这说明276家中小上市企业在获利能力、营运能力、偿债能力、发展能力等方面具有不同的特点和发展实绩。

三、模型构建与结果分析

将这276家公司分为两类，即正常公司和ST公司，并分别用1和-1界定。2009年6月，深交所完成了对深市主板和中小企业板上市公司2008年度信息披露的考核工作，并向社会公开了考核结果。其中中小板公司不及格2家，分别是ST琼花(002002)和ST张铜(002075)。

由于新会计准则应用指南列举了商业银行资产负债表的结构，未将资产负债分为“流动”与“非流动”，宁波银行(002142)的报表未区分“流动资产”与“非流动资产”，所以“流动资产周转率”、“现金流动负债比率”两项指标无法计算。因此，可得数据共275个数据对。设可分样本集为{xi，yi}，i=1，2，…，275，其中x∈R10，即 x 是 10 维特征向量，y∈{-1，1}，是类别号。

n维空间线性判断函数的形式可设为:

分类面方程为:

即若集合中的类1和类2线性可分，则存在有(w·a)，使得:

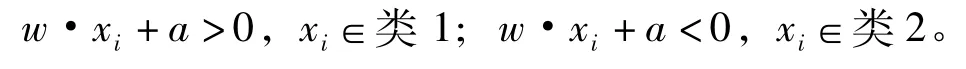
式中w为权向量，a为分类域值。

而n维空间非线性判断的思路则是先通过非线性变换将输入向量映射到一个高维空间中，转换成某个高维空间的线形问题，然后在此高维特征空间中进行分类运算，得到最优分类面。

通过对数据进行预处理后，用支持向量机C-SVC进行分类分析。

给定训练集{xi，yi}，i=1，2，…，l，其中输入数据 x 是一个欧式空间 Rn，y∈{-1，1}，是实数 R 的封闭子集，学习的目标就是构造一个决策函数，将测试数据尽可能正确地予以分类。

借助特定的非线性映射φ(x)，输入x被映射到高维空间。在这个空间上，学习机器能够选择一个特定的函数f(x)，即:

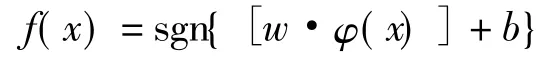
根据推广理论，要解出决策函数f(x)，可考虑经过适当定义的核函数K(，):

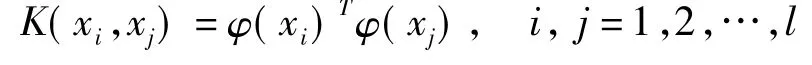
这时，利用支持向量机解决分类问题，就是求下面的优化问题:

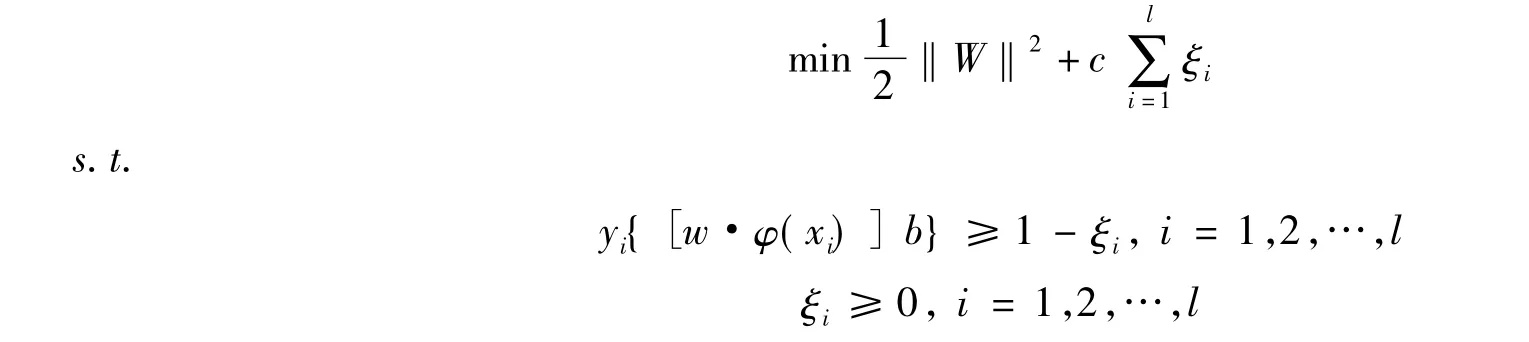
其中，ξi，i=1，2… 为松弛变量。

其对偶问题为:

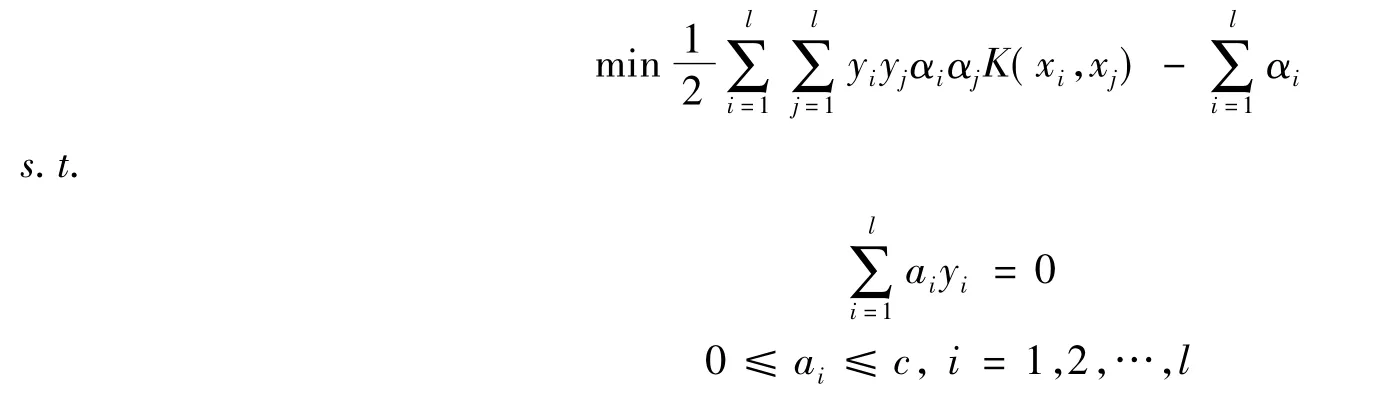
其中，α*=(α*1，α*2，…，α*l)为最优解。

因此，得到:

任何满足Mercer条件的对称函数都可以成为核函数，并可建立不同的学习模型。目前最常使用的核函数为:

Sigmoid 核函数 K(xi，xj)=tanh［v(xi，xj)+c］，where v ＞ 0，c ＜ 0。

并且，任何核函数的非负线性组合仍然是一个Mercer核。一旦核函数确定后，参数γ和σ2(sig2)就可以进一步优化出来。

结果如图1所示:

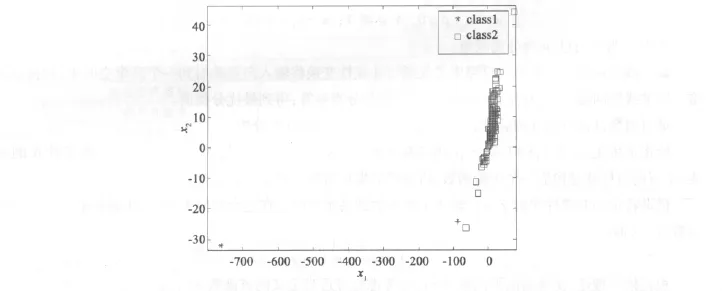
图1 使用C-SVC的函数估计结果

可见用上面的分类模型对训练数据重新进行验证，得出两个公司为-1类即ST类公司，它们分别是ST琼花(002002)和ST张铜(002075)。这个结果与实际相吻合，说明通过支持向量机所建立的决策函数能够被用来评估我国中小上市公司的财务质量。

四、结 论

随着信息时代的不断发展，支持向量机的应用也越来越广泛。在解决处理模式分类问题方面，目前主要应用于图象分类、文本分类、手写字符识别、生物数据分析等。随着智能算法的发展，在企业财务评价模型研究还不够成熟的今天，应用和加强基于支持向量机财务评价模型的研究很有必要。本文以2009年276家中小上市公司为研究对象，在对企业财务获利能力、营运能力、偿债能力、发展能力等四个方面分析的基础上，以其财务数据作为输入特征向量，运用支持向量机的方法构建出中小上市公司企业财务绩效评价模型，经实证分析，该模型分析的结果与样本企业实际情况基本相符，进一步验证了模型的准确性和可操作性。运用支持向量机的方法构建的财务评价模型，摆脱了传统模型依赖线性函数建立判别模型的限制，有效解决了有限样本、非线性、高维识别等实际复杂问题，而且该模型人为设定的参数少，具有简洁的数学形式和直观的几何解释，便于理解和应用。

［1］李云飞，李鹏雁.基于GA-SVM的上市公司财务评价模型研究［J］.燕山大学学报，2011(3):184-187.

［2］阎娟娟，孙红梅，刘金花.支持向量机的上市公司财务危机预警模型［J］.统计与决策，2006(6):158-159.

［3］吴德胜，殷尹.不同模型在财务预警实证中的比较研究［J］.管理工程学报，2004(2):105-108.

［4］杨淑娥，康伟刚.上市公司财务预警模型Y分数模型的实证研究［J］.中国软科学，2003(1):57-60.

［5］PENDHARKAR P C.A Threshold Varying Artificial Neural Network Approach for Classification and Its Application to Bankruptcy Prediction Problem［J］.Computers&Operations Research，2005，32(10):2561-2582.

［6］BACK B，LAITINEN T，SERE K.Neural Networks and Genetic Algorithms for Bankruptcy Predictions［J］.Expert Systems with Applications，1996，11(4):407-413.

［7］YANG Z R，PLATT M B，PLATT H D.Probabilistic Neural Networks in Bankruptcy Prediction［J］.Journal of Business Research，1999，44(2):67-74.

［8］ZHANG G，HU M Y，PATUWO B E，et al.Artificial Neural Networksin Bankruptcy Prediction:General Framework and Crossvalidation Analysis［J］.European Journal of Operational Research，1999，116(1):16-32.

［9］沈明华，肖立，王飞行.支持向量机在模式识别中的应用［J］.电讯技术，2006，46(4):9-12.

［10］周晓斌，崔宝同.企业财务状况评价模型研究［J］.边疆经济与文化，2008(5):27-29.

［11］何晓庆，李腾基.基于支持向量机财务预警模型的实证研究［J］.中小企业管理与科技(上旬刊)，2011(9):143-144.

［12］安欣，苏时光，王韬，等.复合支持向量机方法及其在光谱分析中的应用［J］.光谱学与光谱分析，2007(8):1619-1621.

［13］于之英.企业财务能力评价模型及其运用［J］.中国集体经济，2011(5):54-155.

［14］刘倩.企业财务绩效评价模型构建——基于主成分分析法［J］.生产力研究，2010(6):249-254.

［15］李晓，李娜，余玉苗.企业财务能力评价模型及其运用［J］.财会通讯，2005(7):73-73.

［16］徐绪堪，周彤.企业财务能力的综合评价模型［J］.统计与决策.2007(3):159-160.

［17］孙毅.上市公司财务报表评价模型研究［D］.北京:北京交通大学，2008:10-14.

［18］袁志发，周静字.多元统计分析［M］.北京:科学出版社，2002:22-26.