基于主成分分析基本原理的经济指标的筛选方法

张 辉，赵秋红

(1山东财经大学统计学院，山东济南 250014;2北京航空航天大学经济管理学院，北京 100191)

一、引 言

在社会、经济及管理等方面的研究中，指标是我们研究对象的内在本质的外在表象，是认知规律有表到里、由浅到深的起点。在初始阶段，为了认识更加全面，我们往往尽可能多的搜集相关指标，但过多的指标也会带来信息的重叠和掩盖。因此，面对较为庞杂的指标数据，我们首先要进行科学合理的筛选，其基本原则为:在指标的可获得性前提下，保证入选指标符合特异性、敏感性、代表性、全面性和简明性［1］。

常见的指标筛选方法有变异系数法、相关分析法、指标聚类法等客观的统计方法和德尔菲法等主观方法，实际工作中，多半是上述几种方法的组合或分阶段应用，如张力军和罗珍［2］首先将评价对象分为几个基本方面，从中分别选出若干个候选指标，再利用聚类分析把指标群分成更小的子类，并通过相关分析方法从子类中选择代表性指标。崇明和丁烈云［3］着眼于指标对系统整体功能影响力的数量化刻画，提出了利用相关分析将一个实际系统抽象为图的方法，将系统核理论与关联聚类分析相合，建立了系统关键指标的选择模型。徐映梅和丁俊君［4］依据相关系数及其聚类分析，将相关程度不同的指标聚为不同的组或类，然后在相关系数高度相关的指标组进行格兰杰因果关系分析，或者利用相关时间序列建模方法中的向量自回归模型及其脉冲响应函数和方差分解分析，选取那些作为原因的变量或指标。这些新的理论和方法的应用无疑是可贵的和富有启发性的，但受其较深的专业知识背景和繁琐步骤所累，其推广和普遍应用恐怕还要假以时日。以多元数据分析见长的主成分分析也在指标筛选中有着不少使用，其主要做法是:赵丽萍和徐维军［5］在求出协方差阵或相关系数阵的特征值与特征向量的基础上，找出近似为零的最小特征值所对应的特征向量中最大分量所对应的指标，将其删除，然后在剩余的指标变量中继续作主成分分析，并采取同样的删除处理方法，经过有限次主成分分析后，直到最小的特征值不是很小为止，用保留下的指标构成指标体系。但实践中，我们感觉此法操作繁琐，如本文实例中，在27个原始指标中，同样选9个指标的情况下，该法要做十八次主成分分析。其次，该文的基本想法是通过主成分分析，找出并删减冗余指标，但我们认为指标去留的依据主要是指标相对于系统整体的影响，而该法在筛选过程中，越往后，被筛减去的指标，就越是割裂了和系统整体的联系，其合理性值得商榷。鉴于此，本文依据主成分分析的基本数学原理，给出了更为直接并且简单易行的经济指标的筛选方法。

二、基本原理及步骤

(一)主成分分析的基本原理

设X=(X1，X2，…，Xp)'为由p个标准化的指标组成的p维随机向量，其相关系数矩阵Var(X)=V≥0，考虑p个变量的线性组合:

易见 Var(Zi)=a'iVai，COV(Zi，Zj)=a'iVaj(i≠j)

则称Z1是X的第一主成分。Z1是在X的所有线性组合中最能综合p个变量信息的一个特殊的线性组合。

一般地，若Zi=a'iX满足:

则称Zi是 X 的第 i个主成分(其系数构成的向量称为特征向量)，i=1，2，…，p［6］。

由定义，可推得主成分的以下几个性质［7］:

性质1:主成分表现为原始变量空间的p个垂直方向轴。

性质2:第一主成分在原p个变量的任何单位长度线性组合中具有最大方差，第j个主成分在与前面j－1个主成分正交的单位长度的线性组合中方差最大。

性质3:前j个主成分在原始变量的任意单位长度的线性组合集合中含有最大的综合方差。

(二)指标筛选方法的原理与步骤

假设待选指标有p个，以下是指标的筛选过程和原理介绍。

(1)对指标数据作标准化处理，以消除量纲影响。

(2)主成分分析与指标初选。

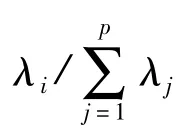
具体做法:在每个主成分中留取较大系数(按绝对值)所对应的那些指标。这使得保留的指标都是与该主成分相关性较强的指标，而删去的都是对该主成分的影响可忽略不计的冗余信息;并且，性质1所反映的主成分之间的正交性，保证了留用的这k批指标中，批与批之间信息不重叠。留取的指标个数可依据各个主成分的方差贡献率来确定。性质2和性质3则使得这k批指标最大限度地保留了原有的指标信息，达到了全面性和代表性的要求。

(3)依据相关性的指标筛选。

应该注意到，批内指标之间有可能有较高的相关性，造成信息重叠、指标重复，对此，主成分析的最具价值的“客观性”(主成分的用方差贡献率来刻画的方差最大性和主成分间的正交性正体现了这一点)已显得无能为力。对此，可用相关分析法删减重复性的指标，即计算任意个评价指标Xi与Xj之间的简单相关系数rij，规定一个用于删减的临界值r0(0＜r0＜1)，如果rij＞r0，则根据重要性的主观判断，删除Xi与Xj中的一个;否则，两个皆留用。由于主成分分析中的相关差阵V恰恰提供了所有p个指标中两两之间的相关系数，这就大大方便了用相关分析法对批内重复性指标的删减。

下面通过实例来详细介绍如何应用该方法进行指标筛选。

三、指标筛选实例

(一)淄博市五区三县经济实力的评价指标的筛选

1.指标筛选

数据来自《山东统计信息网》淄博市五区三县2007年27个主要经济指标，分别用X1—X27表示(见表1)。

表1 淄博市五区三县2007年主要经济指标

为了建立反映淄博市各区县经济实力的评价指数并给出排名，首先从这27个主要经济指标中筛选出符合前面所提筛选原则的指标体系。具体步骤和方法如下:

(1)将27个经济指标作标准化处理。

(2)对标准化后的27个经济指标做主成分分析。分析结果见表2、表3。

从表2看，前三个主成分的方差的累计贡献率已达89.04%，说明前三个主成分基本包含了全部的指标具有的信息。为了方便挑选指标，将三个特征向量依照各自的分量大小降序排列(见表3)。

表2 相关系数矩阵的特征值及方差贡献率

表3 相关系数矩阵的特征向量(依照分量大小降序排列)

表3第一主成分中，X12、X10、X4、X14、X11、X13的系数均小于 0.1，同样情况出现于第二主成分中的 X18、X19、X15、X17、X16、X10、X3、X7、X20、X7、X21、X22的系数和第三主成分中的 X23、X4、X21、X22、X27、X8、X2的系数。这表明这些变量对各自所在的主成分的影响可以忽略不计，从而可以从各自所属批次中删去。由于第一、二、三主成分的方差贡献率分别是57.02%、19.03%、13.00%，据此，初选指标在三个主成分中的选取个数分别定为10、4和3。在前3个主成分中，由于系数绝对值分别处于前10、4、3位，因此，第一主成分中选取前10个指标(X5、X21、X19、X11、X8、X16、X18、X17、X7、X20)，第二主成分中选取前 4 个指标(X2、X4、X11、X13)，第三主成分中选取前3 个指标(X10、X12、X14)。

(3)在这三个批次的初选指标中，用相关分析法做进一步的筛选。表4、表5、表6分别为第一、二、三批次的各10个、4个和3个指标间的相关系数表。

由于样本量容量仅为8，我们认为上述任意两指标间的相关系数还不足以反映这两指标变量间实际的相关性，所以把相关视作样本数为8的皮尔逊样本相关系数，对它们须进行相关性的统计检验。其置信水平为0.05的双尾检验的临界值是0.707，即若样本相关系数绝对值超过0.707，便可认为这两个指标变量之间存在显著的线性相关，否则，就不相关［10］。在数轴上临界值0.707和绝对相关值1之间，我们把它平均分为前、中、后三段，分别称为相关、中度相关和高度相关区域。当两指标间相关系数处于区间［0.9，1)时，我们视作高度相关，若经济意义相近，则根据重要性的判断删减为一个(或者基于因果关系的判断而留“因”去“果”);若经济意义差别较大(或因果关系难以判别)，则都保留。

表4 第一批次指标间的相关系数

考察第一批次的指标(见表4，自上而下):

①X5(地方财政预算内收入)与X19(规模以上工业企业利税总额)、X16(规模以上工业企业工业总产值)、X18(规模以上工业企业利润总额)、X17(规模以上工业企业主营业收入)均高度相关，但与这些指标的含义差异较大，故暂不作删除。

②X21(出口总额)与X22(城镇固定资产投资完成额)高度相关但经济意义迥异，故暂不作删除。

③X19分别与X16、X18、X17高度相关且它们的指标含义相近，X19与X18、X19与X17之间权衡取舍，我们皆选X19，而 X19与 X16之间权衡取舍，选 X16。故本轮我们筛选出了 X5、X21、X22、X8、X16、X7、X20参与下轮筛选。

④X22分别与 X8、X16、X7、X20的相关系数均低于 0.95，故不作筛减，本轮依旧是以 X5、X21、X22、X8、X16、X7、X20参与下轮筛选。

⑤X8(城乡居民储蓄存款余额)分别与X7年末金融机构各项贷款余额)、X20(社会消费品零售额)高度相关;X8与X7指标含义相近，两者间权衡，取X7舍X8。X8与X20指标意义迥异，保留X20。本轮我们筛选出了X5、X21、X22、X7、X20参与下轮筛选。

⑥X16分别与 X7、X20的相关系数均低于 0.95，故不作删减，本轮依旧是以 X5、X21、X22、X8、X16、X7、X20参与下轮筛选。

⑦X18、X17已被删除，不再考虑。

⑧X7(年末金融机构各项贷款余额)与X20(社会消费品零售额)高度相关且含义差异较大，但考虑若不作删减，保留的指标会达6个，稍嫌过多，因此权衡二者，舍X7取X20。

综上，在初选的第一批次的10个指标中选定了X5、X21、X22、X16、X20。

表5中X11(油料产量)与X15(水果产量)高度相关，留X11删去 X15;X4(乡村从业人员数)与X11相关系数为0.5837，低于检验临界值，皆保留;X2(行政区域土地面积)与 X4、X11、X13均高度相关，说明，X4、X11、X13在淄博市均受自然禀赋条件X2的直接影响。故第二批次的初选指标中只取X2这一个指标。

表6中X10(粮食总产量)、X12(蔬菜产量)、X14(肉类总产量)这三个指标两两间的相关系数均小于检验临界值，皆保留。

表5 第二批次指标间的相关系数

表6 第三批次指标间的相关系数

综上，考察淄博市五区三县2007年经济发展状况的指标体系可由如下9个指标构成:X2、X5、X10、X14、X16、X20、X12、X21、X22。

2.指标的应用与验证

为验证这9个指标能否全面反映淄博市的经济状况，我们用它来合成淄博市五区三县2007年综合经济实力的评价指数。思路为:将9个指标数据Xi标准化为X^i，然后进行因子分析;根据相关阵的特征向量的累计贡献率确定因子个数，再由各因子具有高载荷的指标含义，找出各因子的解释意义;接着，计算各区县在每个因子上的得分，再以各因子的方差贡献率为权重对各个因子作加权平均。每个区、县的加权得分即为该区、县的综合经济实力的评价指数。分析过程和计算结果如下。

表7 相关系数矩阵的特征值和贡献率

由表7知，前两个特征向量的累计贡献率已达82.52﹪，取这两个为主因子。

表8是经过正交旋转后的因子载荷阵。可知F1(因子1)在指标X5(地方财政预算内收入)、X21(出口总额)、X22(城镇固定资产投资完成额)、X16(规模以上工业企业工业总产值)、X20(社会消费品零售额)上有较大载荷，可视为经济总量因子。F2(因子2)在指标X10(粮食总产量)、X12(蔬菜产量)、X14(肉类总产量)上有较大载荷，可看作农业因子。由于因子载荷是载荷值对应变量与因子的相关系数，由表7可分别知构造因子1和因子2的评价指数即F1和F2:

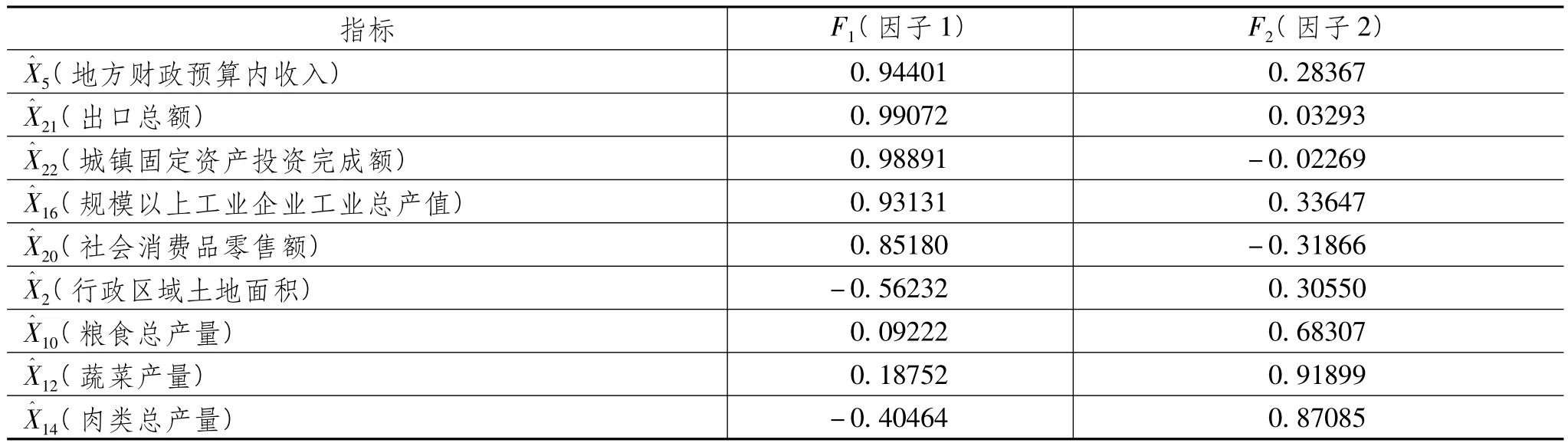
表8 旋转后的因子载荷矩阵

以这两个因子的方差贡献率(见表7)为权重对它们作加权平均，即得两因子的综合评价指数:

F=0.5519F1+0.2733F2

将各区县的指标体系中标准化后的9个指标，分别代入这三个指数公式(见表9)，可得它们在各个因子上的得分和综合得分以及排名［11－13］。

表9 各区县的因子得分及排名

从综合因子的权重来看，影响淄博市区、县综合经济实力的首要因素是以财政收入、出口、投资和工业产值、消费为代表的经济总量因子，由于财政收入、出口、投资都工业产值高度相关，消费与工业产值也相关，因此，在对总量因子的考察中，工业生产水平占有重要的地位;而农业发展因子表现为对总量因子的修正和微调。这与淄博市是全国重要的门类较齐全的老工业基地而县域经济正起步发展的实际状况相吻合的，表8真实客观的体现了这一点。这一方面说明了评价指数编制方法的正确性，也验证了本指标筛选方法的适用性。

(二)中国宏观经济运行质量评价指标的筛选

1.一种基于Granger因果关系检验的指标筛选法

文献［4］为了筛选出在规模速度方面对宏观经济运行质量进行评价的指标，从《中国统计年鉴(2005)》上收集了1985－2004年的16个规模速度指标(见表10)，首先对这些指标进行相关分析和R型聚类，然后在每类中对指标进行 Granger因果关系检验，筛选出了下面 8 个作为原因的评价指标:X1、X3、X4、X5、X6、X7、X13、X16。

表10 16个规模速度指标［4］

2.本文方法的指标筛选

为了作对比，我们应用本文方法对同样的数据进行筛选。

以文献［4］得出的相关阵为出发点做主成分分析。过程和结果见表11—表15。

由表11可知，原数据的前4个主成分的方差累计贡献率已达85.98﹪，故取前4个主成分作分析，并且依据4个主成分的方差贡献率，在前4个主成分中确定初选的4批指标的个数分别为:7、3、3、1。

在表12中，依据所对应分量绝对值大小和4个批次的指标个数，由前4个主成分初选出的指标分别为，第 1 批次:X10、X3、X11、X12、X13X16、X14;第 2 批次:X2、X1、X6;第 3 批次:X8、X7、X9第 4 批次:X4。在每批内依据相关性再对它们进行筛检。

表11 相关系数矩阵的特征值及方差贡献率

由于样本量容量为20，我们把相关视作样本数为20的皮尔逊样本相关，对它们进行相关性的统计检验。其置信水平为0.05的双尾检验的临界值是0.378，在数轴上临界值0.378和绝对相关值1之间，我们把它平均分为前、中、后三段，分别称为相关、中度相关和高度相关区域，因此，当两个指标的相关系数处于区间［0.78，1)时，定义为高度相关。

依据表13，自上而下，第一批次初选指标的筛选过程如下:

(1)X3分别与X10、X11、X13高度相关。其中，X3与X10含义相近，就评价宏观经济运行质量来说，X3比X10重要，故留X3舍X10;X3与X11、X13的指标含义差异较大，故一同保留。

(2)X10已删除，故不再考虑与其它指标的相关性。

(3)X11分别与 X12、X13高度相关且指标含义相近，X11分别受制于 X12、X13，故删掉 X11，而保留 X12、X13。

(4)X12与 X13、X16高度相关。由于 X13的波动可传导至 X12，故可视 X13为“因”、X12为“果”;X12与 X16存在着相互作用，但我们认为X16对X12的作用更强。因此删掉X12，保留X13、X16。

经过以上过程，除去删掉的，剩下的即为第一批次入选指标:X3、X13、X16。

表12 协方差矩阵的特征向量(依照分量大小降序排列)

依据相关性，由表14可知，第二批次入选指标为:X1、X6或X2、X6;由表15可知，第三批次入选指标为:X7、X9或X8、X9。显见，第四批次为:X4。就评价宏观经济运行质量来说，GDP增长率(X1)比固定资产投资增长率(X2)重要，财政收人增长率(X7)比财政支出增长率(X8)重要，故最终入选的是，第一批次为:X3、X13、X16、X14;第2 批次为:X1、X6;第 3 批:X7、X9;第 4 批次为:X4。

表13 第一批次指标间的相关系数

表14 第二批次指标间的相关系数

表15 第三批次指标间的相关系数

3.两种方法的结果对比

文献［4］选出了 8 个指标:X1、X3、X4、X5、X6、X7、X13和 X16。本文方法选出了 9 个指标:X1、X3、X4、X6、X7、X9、X13、X14、X16。二者对比，共同的指标高达7个，方法虽迥然不同，结果却堪称殊途同归，异曲同工。比较之下，显见本文方法的简易、可行。

四、结 论

本文指标筛选方法充分应用了主成分的方差最大性和正交性，并在相关分析法筛选法中融入了基于研究背景的主观价值判断，具有以下几个优点:

1.可操作性强。

2.理论根基扎实。如正交性保证了批与批之间指标的信息不重复，方差最大性保证了主成分对系统重要信息的保留和次要信息的忽略等。

3.便于统计和经济意义上的解释。

4.定量和定性分析相结合。定量为主，定性辅之，两者之间做到了取长补短。

虽然主观判断的因人而异会使得最后入选指标有差异，但是，因为定性分析只局限于同类指标中两两之间的选择，主观判断出错的可能性大大降低;即使在两指标之间做出了不同选择，由于它们高度相关而互有替代性，故不会有太大偏差;同时也避免了单纯的定量方法对指标经济含义的完全忽视。这种定量和定性的结合充分体现了《大不列颠百科全书》对统计学的描述:“统计学是收集和分析数据的科学与艺术”，此处的“艺术性”更是得到了已故著名统计学家陈希孺院士的高度认可:“这里所强调的艺术性，是为着重说明统计方法需要灵活使用，很依赖于人的判断以至灵感，强调这一点很有好处，它提醒人们不能以教条式的方法态度来看待数理统计方法，以为只要记住一些公式和方法，碰到什么问题套上去就行。”［14］

［1］何圣.上海劳动关系综合评价指标体系构建及应用研究［D］.上海:复旦大学，2007.

［2］张立军，罗珍.上市公司经营业绩评价指标的筛选方法［J］.统计与决策，2008(18):63－65.

［3］李崇明，丁烈云.复杂系统指标筛选模型及其在武汉市房地产系统中的应用［J］.统计研究，2008(10):40－45.

［4］徐映梅，丁俊君.宏观经济运行质量评价指标的选择方法［J］.中南财经政法大学学报，2OO7(10):3－8.

［5］赵丽萍，徐维军.综合评价指标的选择方法及实证分析［J］.宁夏大学学报(自然科学版)，2002(6):144－146.

［6］张尧庭.方开泰著.多元统计分析引论［M］.北京:科学出版社，1982.

［7］张辉.经济周期波动的灰色统计方法［D］.济南:山东师范大学，2003.

［8］王惠文.用主成分分析法建立系统评估指数的限制条件浅析［J］.系统工程理论与实践，1996(9):24－27.

［9］RICHARD A，JOHNSON，DEAN W ICHERN.实用多元统计分析(6 版)［M］.陆璇，叶俊，译.北京:清华大学出版社，2008.

［10］FREDERICK J，GRAVETTER，LARRY B，WALLNAN.行为科学统计(7 版)［M］.王爱民，李悦，等，译.北京:中国轻工业出版社，2008.

［11］何有世，徐文芹.因子分析法在工业企业经济效益综合评价中的应用［J］.数理统计与管理，2003(1):19－22.

［12］ZHENG CH M.The Evaluation on the Industrial Competitiveness of Beijing［C］//International Conference on Internet Technology and Applications.ITAPP.2010.Page(s):1 －5.

［13］TUNG，CHE TSUNG，YU JE LEE.Expert Systems with Applications［M］//The Innovative Performance Evaluation Model of Gray Factor Analysis:A Case Study of Listed Biotechnology Corporations in Taiwan.VOL 37 ISSU 12 PAGE 7844－7851 DATE 2010.

［14］陈希孺.数理统计学简史［M］.长沙:湖南教育出版社，2002.

［15］李秀荣，杨芳，焦玉志.基于主成分分析的山东省现代服务业发展水平综合评价［J］.山东财政学院学报，2012(3):100－108.

［16］周新秀，刘岩.城乡融合发展评价指标体系的构建与应用——以山东省为例［J］.山东财政学院学报，2010(1):87－89.