ΣΔ微加速度计中基于脉宽调制的力反馈回路*

陶呈瑶 ，邓康发

(1.中国科学院地质与地球物理研究所/海外高层次人才创新创业基地，北京100029;2.中国科学院大学，北京100049;3.北京大学微电子学研究院微米/纳米加工技术国家级重点实验室，北京100871)

加速度计能将加速度物理信号转为电学信号，被广泛用于制导、汽车、地震数据的采集等领域。基于微机电系统(MEMS)技术制作的电容式微加速度计成为微传感器领域的研究热点［1－4］。

传统电容式微加速度计采用开环设计，在质量块变形较大情况下，输出会出现非线性，从而降低加速度计精度。为提高系统的灵敏度，带宽，动态范围等性能，微加速度计通常采用静电力反馈方式。此时引入静电力反馈回路，在质量块变形较大条件下，通过电压调节，质量块能迅速回到平衡位置。加速度计的反馈可分连续反馈和数字分时反馈，而分时反馈则可细分成模拟反馈和 Sigma-Delta(ΣΔ)调制反馈［5－8］。相比与模拟反馈，ΣΔ调制反馈噪声容限大，直接数字输出，无需额外ADC;同时采用1 bit数字反馈能够大大降低静电力非线性问题。因此，我们选用了ΣΔ调制反馈方案实现微加速度计的接口电路。

然而ΣΔ调制反馈的微加速度计系统设计复杂度较大，如需要考虑机电耦合，电学信号设计到模拟和数字信号，数字处理需要高频时钟［10］。例如，针对静电力反馈回路，需要将ΣΔ调制器生成的脉宽调制(PWM)数字信号转换为模拟电压，从而给微加速度计提供静电力。一般采用数字滤波+降频+数模转换的方案［9］:首先 PWM波经过数字滤波器(Sinc3和FIR滤波器)和降频器，滤除高频信号，降低有效数字信号的频率，之后经过数模转换器，将数字信号转换为模拟信号，如图1所示。这种方案需要经过3个模块才能实现模拟信号输出，资源开销大，结构复杂。

图1 静电力反馈回路示意图

为了降低力反馈回路的结构复杂度，我们提出一种模拟滤波方案:借助一个模拟滤波器，可以将PWM数字信号直接转为模拟信号［11－14］。此方案的模拟滤波器既有滤波作用，也有数模转换器功能，结构简单易实现。本文先根据如带宽，截止频率等参数建立力反馈回路的Simulink模型，进行系统级仿真，之后采用Filter Solutions滤波器设计软件确定为三阶低通巴特沃斯滤波器，并采用Pspice仿真软件进行电路级仿真。最后将制作的PCB版电路进行测试与分析。

1 工作原理

基于ΣΔ调制的电容式微加速度计系统如图2所示。微加速度计一般有上下电极板，中间是质量块，其中上极板与质量块构成电容C1，而下极板与质量块构成电容C2;当质量块往上偏移，则上极版与质量块的电极间隙变小，电容C1变大，C2变小;之后通过电荷积分器实现电荷/电压转换，再经过积分器，零阶保持器和量化器，产生数据流，输出PWM波。两个DAC实现两条反馈回路:第1条静电力反馈回路，其中DAC能将反馈电压转化为加速度计上的静电力，这个称为机电DAC;第2条电学反馈回路，其中DAC给电学积分器提供电学反馈信号。

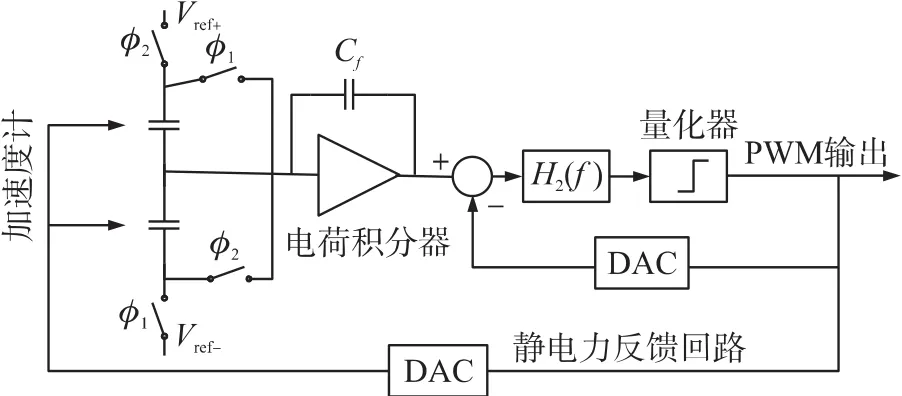
图2 微加速度计的机电混合ΣΔ调制电路

下面将借助PWM波形特点制作上述机电DAC。PWM波是一种周期一定而高低电平的占空比可以调制的方波信号，该PWM的高低电平分别为VH和VL，如图3所示。

图3 基于PWM的DAC模块的工作原理

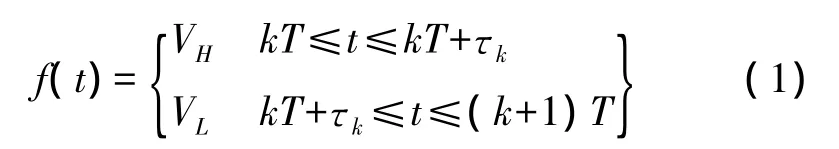
其中k表示PWM波的第k个周期，T是PWM方波的基本周期，τk是PWM波第k个周期中高电平的时间长度。把式(1)所表示的函数展开成傅里叶级数，得到式(2):

从式(2)可以看出，式中第1个方括弧为直流分量，第2项为n次谐波分量之和。式(2)中的直流分量与τk成线性关系，并随着τk从0到T，直流分量也从VL到VL+VH之间变化，这正是模拟电压输出所需要的。因此，如果能把式(2)中除直流分量的谐波过滤掉，则可以得到从PWM波到模拟电压输出的数模转换，即PWM波可以通过一个低通滤波器进行解调。对于静电力反馈回路，借助PWM本身特点，后端加上模拟低通滤波器，能将PWM波(数字信号)转换为平滑的模拟电压信号，此时低通滤波器即有滤高频波的作用，又相当于一个数模转换器(DAC)，如图3所示。在ΣΔ调制中，PWM信号的频率要远高于奈奎斯特抽样速率，此时PWM信号的频率越高，对滤波器的阶数要求越低，因此合适的滤波器越容易实现。相比图1的传统方案，此方案省去数模转换器的设计，从而降低电路结构复杂度。同时模块的简化，有利于降低反馈回路的延迟时间，从而提高整个负反馈系统的频率响应。因此，下文将具体描述基于脉宽调制的力反馈回路的设计思路。

对应的的PWM波形可以用分段函数表示为:

基于PWM的DAC应用中，分辨率nbit是一个很重要的参数，这个主要决定于PWM波的基本周期T和PWM波能够实现的最小占空比，即高电平最小时间长度τmin，则DAC的分辨率(即模拟信号分辨率)可表示为:

2 力反馈回路的设计与仿真

2.1 方案选择

由于输入信号带宽为3.4 kHz，则奈奎斯特采样率至少为6.8 kHz;过采样率设置为64，则PWM波频率为435.2 kHz;低通滤波器的截止频率设置为 3.4 kHz。

基于脉宽调制的力反馈回路中最关键的是模拟低通滤波器。通过低通滤波器后，主要考虑的是一次谐波影响，再后面的谐波影响加起来都小于一次谐波影响。因此，如果能把一次谐波很好过滤掉，则高次谐波的影响就可忽略不计了。一次谐波的频率f1为 435.2 kHz，需要将一次谐波的影响消除到1/2nbit，即低通滤波器在频率f1处，其频率对应的电压增益要在以下。假设 n为8bitbit，其频率响应的电压增益要在－52.08 dB。假设选用一阶低通滤波器，其截止频率为1/2(πRC)，即－52.08 dB。对于一阶低通滤波器来说，带宽外是按照每10倍频程下降－20 dB，可以推导出截止频率应该设置为488 Hz左右，该值远小于要求的信号带宽3.4 kHz，所以不适用。

对于有源低通滤波器，按照通带滤波特性可以分最大平坦型(巴特沃斯型)，等纹波型(切比雪夫型)，线性相移型(贝塞尔型)滤波器。其中巴特沃斯型滤波器的特点是在通带以内幅频曲线的幅度最平坦，由通带到阻带衰减陡度较缓，三阶低通截止频率以后的衰减速率为60 dB倍频程，相频特性是非线性的。而ΣΔ调制电路的过采样率为64，PWM信号的频率较高，对滤波器的阶数就要求较低。因此选用三阶低通巴特沃斯滤波器则足够。

2.2 系统级仿真

基本模型如图4所示，为简化模型，先不考虑加速度计的二阶模型，只关注ΣΔ调制器模块。其中三阶低通巴特沃斯滤波器的传递函数:

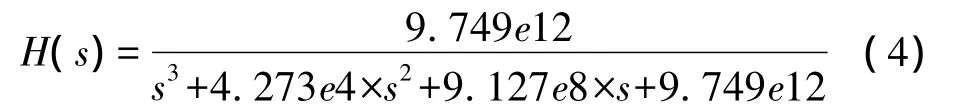
对应的截止频率为3.4 kHz。

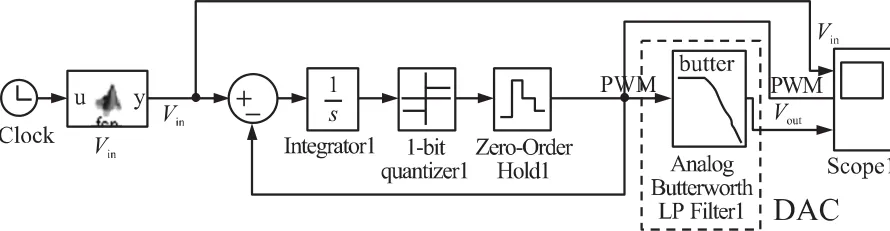
图4 DAC模块的Simulink模型

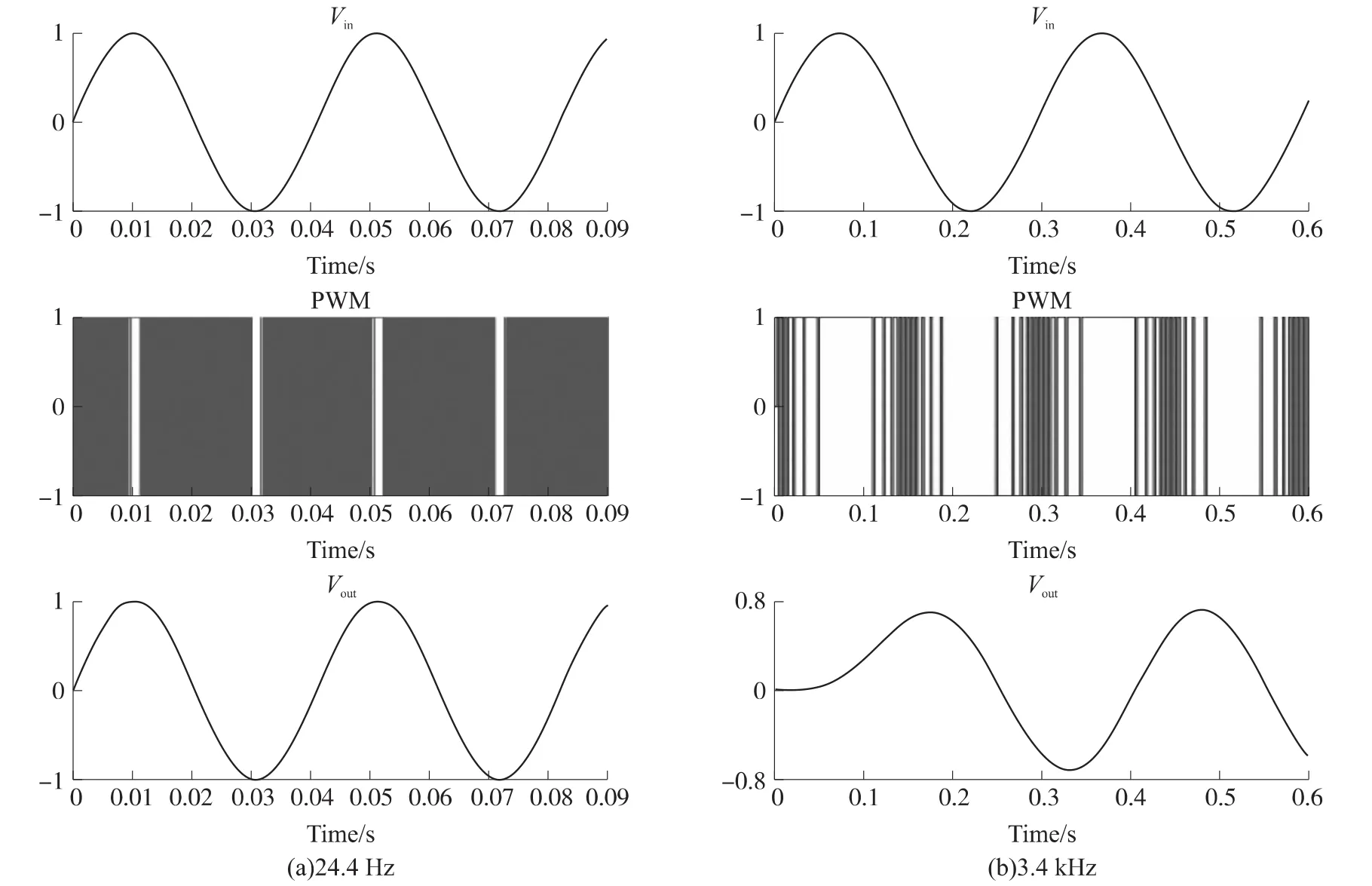
图 5 Vin频率(a)24.4 Hz、(b)3.4 kHz的仿真结果

当正弦波输入信号Vin的频率为24.4 Hz时，ΣΔ调制器的采样频率为435.2 kHz，对应的PWM波和模拟输出信号Vout如图5(a)所示，可以看出模拟输出信号平滑无失真，并且与输入信号没有相位差。当输入信号Vin的频率为3.4 kHz时(即滤波器的截止频率)，如图5(b)所示，模拟输出信号Vout平滑高保真，但是幅值衰减至输入幅值的70.7%左右，也就是衰减3 dB，相位差约为135°。这是由于输入信号频率接近低通滤波器的截止频率，造成信号衰减。

接下来将上述方案移植到加速度计的Simulink模型中［15］，如图6所示。其中加速度计模型是个二阶系统，输入的惯性力和力反馈回路中的静电力的差值经过此二阶系统转换为质量块的位移，对应的两个电容发生变化，再经过C/V转换模块将两电容的差值转换为电压，之后在ΣΔ调制器进行数模转换和噪声调制，输出PWM波。此时PWM信号经过力反馈回路中的低通滤波器和缓冲器可以得到模拟电压Vfb，最后通过电压与静电力转换模块得到反馈静电力，依次形成负反馈系统。

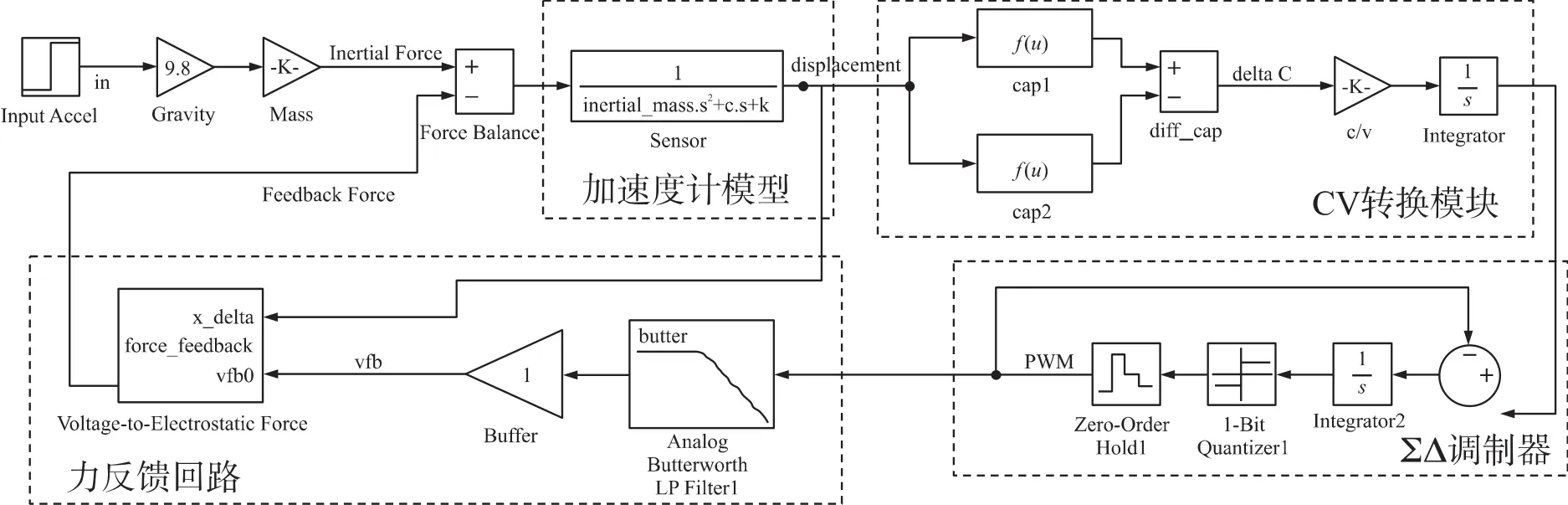
图6 加速度计的Simulink模型

在此加速度计的Simulink模型输入一个阶跃信号，看反馈静电力变化情况，对应的仿真结果如图7所示，其中反馈静电力的响应时间约为9.6 ms，并在稳定条件下，其幅值(9 μN)与输入惯性力相同。

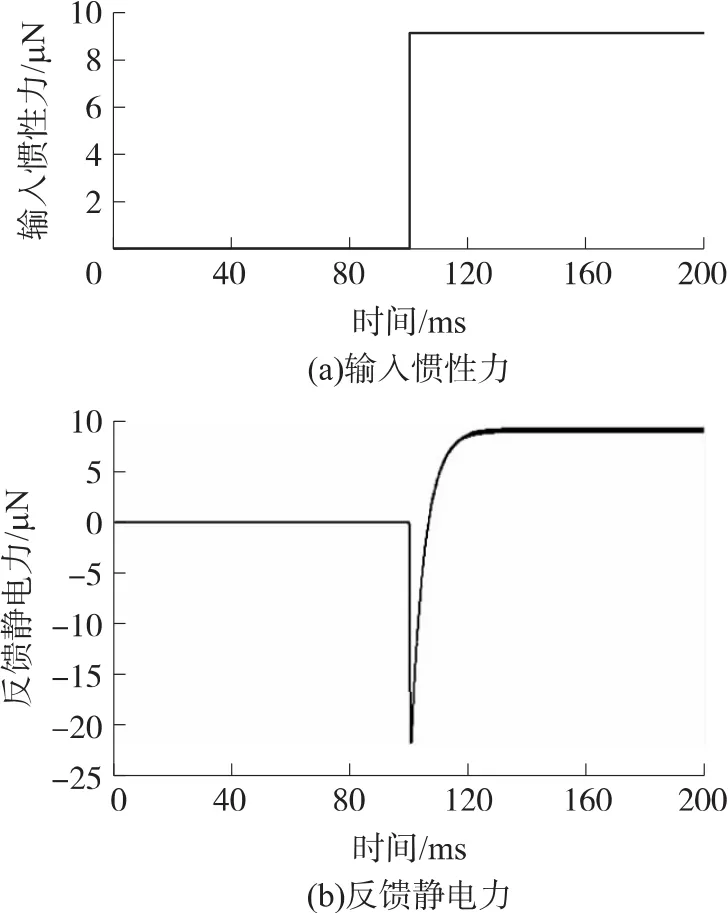
图7 力反馈回路仿真结果

2.3 电路级仿真

先通过Filter Solutions滤波器设计软件，初步确定电路参数。之后采用Pspice仿真并根据实际情况修改电路参数，电路如图8(a)所示，放大器采用OP07，双端5 V电源供电。PWM波再经过三阶滤波器得到直流分量，即Sigma-Delta的调制PWM波得到解调，实现了DAC功能。由于放大器OP07的输入阻抗很大，三阶阻容滤波的效果很好，滤波后的电压纹波极小，满足高精度要求。

下面重点检测低通滤波器的性能。输入交流信号，从1 Hz到1 MHz进行扫频，对应的频率响应如下图8(b)所示，可以看到－3 dB对应的截止频率为3.15 kHz。Pspice仿真得到的截止频率(3.15 kHz)小于理论设计的截止频率，主要原因是pspice采用了OP07的器件模型，考虑到了一下集成运放的非理想效应等。

3 测试与讨论

根据上述系统仿真和电路仿真，我们将上述电路原理图进行了PCB制版，如图9所示。我们主要关注力反馈回路的功能特性，即重点考察模拟滤波器和负载驱动电路。我们将借助微处理器和SD卡，将Simulink模型中产生的PWM波形存取到SD卡并由微处理器进行读取并输出PWM波。

对应的电路工作流程如图10所示。先通过Simulink软件进行ΣΔ调制模块仿真，将输出的数据流(PWM)提取并存取到SD卡，而L3S1138微处理器则读取SD卡上存储的信息并将PWM波输出到低通滤波器，得到模拟信号。后续接入负载驱动电路，即加上一级TLV2472轨到轨放大器，工作在电压跟随器方式，最终的输出电压的跨度几乎等于

图8 低通滤波器的电路图和频率响应图

图9 PCB电路图

电源电压幅度。示波器将采集微处理器输出的PWM波信号和经过电压跟随器后的模拟信号。

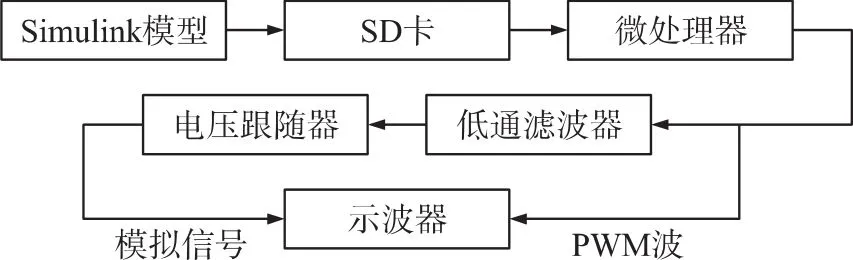
图10 电路工作流程

PWM采样频率为为195.3 kHz，对应的采样周期T为5.12 μs，而微处理器的时钟频率为50 MHz，即对应高电平最小时间长度τmin为0.02 μs，根据式(3)，对应的DAC的分辨率

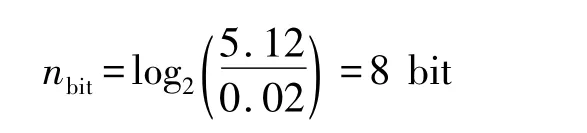
假设力反馈回路的电源电压Vcc为5 V，则输出模拟信号的最小分辨电压

当输入正弦波频率为为24.4 Hz，PWM波和后置三阶巴特沃斯滤波器后的输出波形如图11所示。可以看到输出模拟信号频率为24.37 Hz，与实际输入波形频率的相对误差为0.12%，波形光滑无失真。

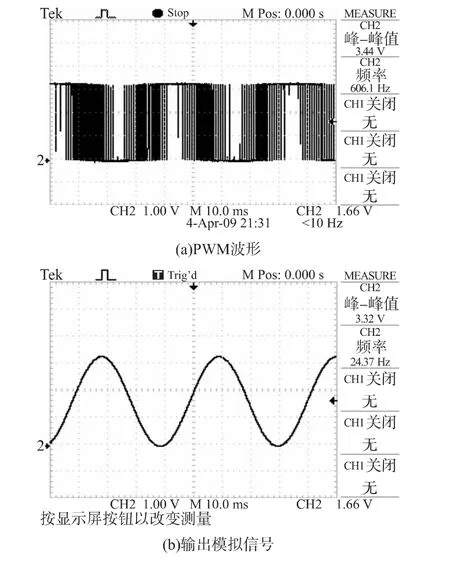
图11 输入为24.4 Hz时PWM波形和输出模拟信号

当输入正弦波为1.953 kHz，经过ΣΔ调制后，通过示波器采集到的数据流如图12(a)所示，经过后置滤波器是三阶巴特沃斯输出波形如图12(b)所示，可以看到输出模拟信号频率1.946 kHz，与实际输入波形频率的相对误差为0.36%，但是输出波形幅值只有输入信号幅值的80%。因此，经过低通滤波器后的输出信号有－1.9 dB的衰减。上述两组数据说明，信号频率越接近低通滤波器的截止频率(3.15 kHz)，其信号幅值就也衰减越大。

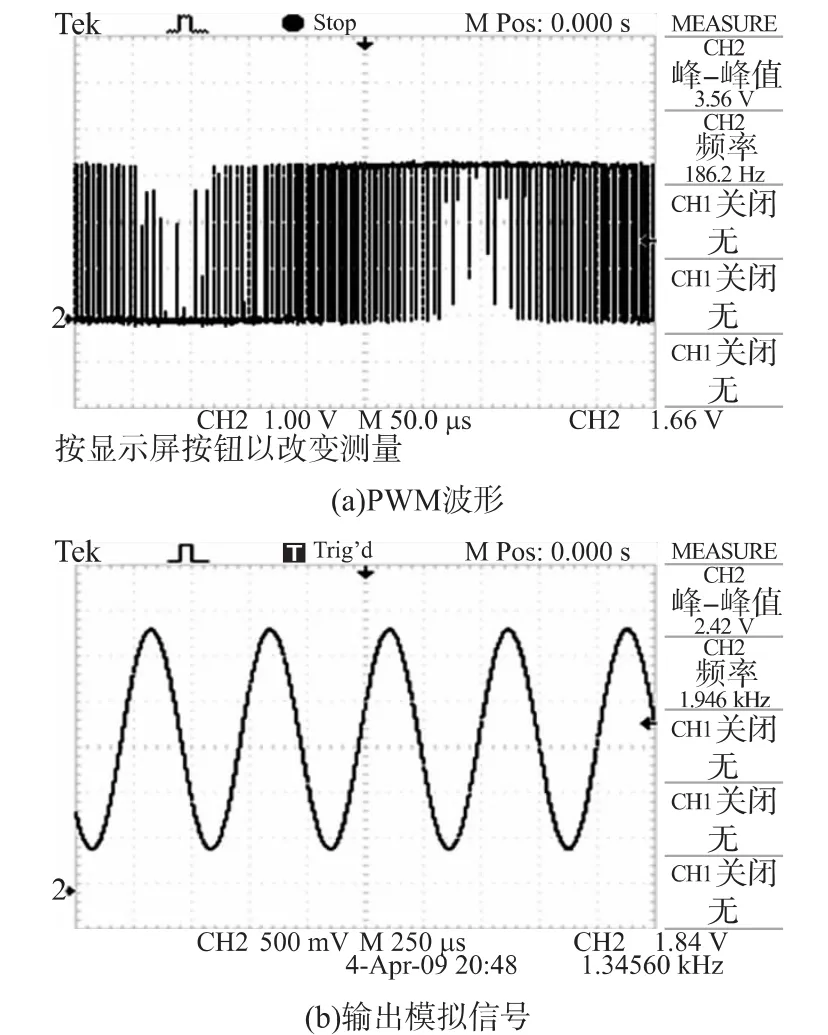
图12 输入为1.953 kHz时PWM波形和输出模拟信号

上述两个试验的结果汇总如表1所示，其中输入信号和输出信号的的频率最大相对误差只有0.36%，满足设计要求，也为下一步ΣΔ调制电路的整体实现打下基础。

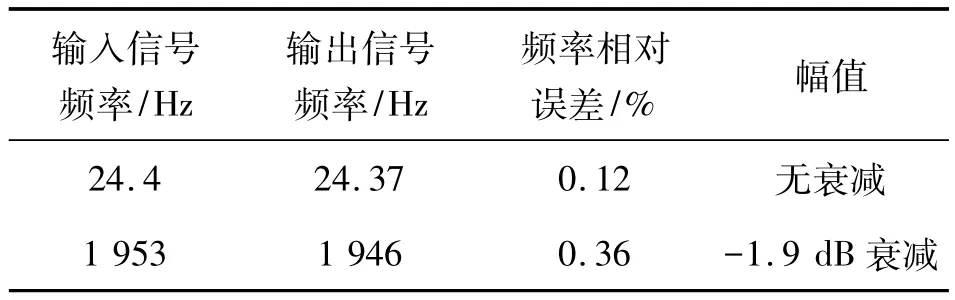
表1 实验结果汇总表

4 总结

本文提出了一种基于脉宽调制的力反馈回路，借助PWM本身特点，后端加上模拟低通滤波器，能将PWM波(数字信号)转换为平滑的模拟电压信号，实现静电力负反馈回路。此方案对模拟滤波器要求低，能以较低复杂度的电路实现高精度的DAC模块。首先分别建立了ΣΔ调制器和力反馈回路的Simulink模型，基于所建模型，设计了微加速度计闭环反馈系统的Simulink模型并进行系统级仿真。之后采用Filter Solutions滤波器设计软件确定三阶低通巴特沃斯滤波器，并采用Pspice仿真软件进行电路级仿真。最后将制作的PCB版电路进行测试:PWM波通过力反馈回路能还原成无失真的模拟信号，输出信号和输入信号的频率相对误差小于0.36%，等效DAC分辨率为8 bit。试验表明，此方案结构简单，成本低，能以较低电路复杂度实现高精度的模拟信号输出，测试结果与理论设计吻合，为下一步ΣΔ调制电路的整体实现打下基础。

［1］Zhou X F，Che L F，Wu J，et al.A Novel Sandwich Capacitive Accelerometer with a Symmetrical Structure Fabricated from a D-SOI Wafer［J］.Journal of Micromechanics and Microengineering，2012，22(8):1－8.

［2］Young D J，Zurcher M A，Semaan M，et al.MEMS Capacitive Accelerometer-Based Middle Ear Microphone［J］.IEEE Transactions on Biomedical Engineering，2012，59(12):3283－3292.

［3］Dong Y，Zwahlen P，Nguyen A，et al.Ultra-High Precision MEMS Accelerometer［C］//Solid-State Sensors， Actuators and Microsystems Conference(TRANSDUCERS)，16th International:，2011:695－698.

［4］Goyal V.Motion‘MEMS’and Its Emerging Automotive Applications［J］.Auto Tech Review，2013，2(7):54－55.

［5］Wu J，Carley L R.Electromechanical ΔΣ Modulation with High-Q Micromechanical Accelerometers and Pulse Density Modulated Force Feedback［J］.IEEE Transactions on Circuits and SystemsⅠ:Regular Papers，2006，53(2):274－287.

［6］Luo J，Ding H，Kraft M.A New Design Methodology for Electro-Mechanical Sigma-Delta-Modulators［C］//Nano/Micro Engineered and Molecular Systems，NEMS 4th IEEE International Conference on 2009:881－884.

［7］Wilcock R，Kraft M.Genetic Algorithm for the Design of Electro-Mechanical Sigma Delta Modulator MEMS Sensors［J］.Sensors，2011，11(10):9217－9232.

［8］Liu Y，Liu X，Wang Y，et al.A Sigma-Delta Interface ASIC for Force-Feedback Micromachined Capacitive Accelerometer［J］.Analog Integrated Circuits and Signal Processing，2012，72(1):27－35.

［9］Kulah Haluk.Closed-Loop Electromechanical Sigma-Delta Microgravity Accelerometers［D］.［Ph.D.Thesis］.Ann Arbor:Engineering Electronics and Electrical，University of Michigan，2003.

［10］吴学忠，肖定邦，李圣怡.电容式微加速度计的闭环检测技术研究［J］.传感技术学报，2006(4):1097－1099.

［11］吴桂清，李泓霖，戴瑜兴，等.微控制器PWM接口实现高分辨率 D/A 转换器方法研究［J］.电子学报，2012(8):1631－1634.

［12］辛德环.传统数模转换器的优缺点分析及高性能PWM-DAC的基本设计思想［J］.机械工程师，2011，10:29－33.

［13］Woodward W.几乎没有纹波的快速稳定同步PWM-DAC滤波器［J］.电子设计技术，2008(8):101.

［14］吴鹏.雷达伺服系统中DAC位数和数字PWM位数的选择［J］.电讯技术，2006(5):178－182.

［15］刘云涛，王颖.Sigma-Delta微加速度计非理想因素建模与系统级设计［J］.传感技术学报，2011，24(11):1532－1537.