水准网自动处理模型及程序实现

付江缺，高万柱，裴良臣

（中南电力设计院，湖北 武汉 430071）

目前结合生产的水准网程序实现不多，主要在于不同行业的数据输入输出格式都不尽相同。专业的软件生产商只能形成通用的版本。本文结合电力行业作业模式，以Matlab语言为基础来对观测数据进行一键式处理［1］，进而实现生产的信息化和自动化。

1 理论基础

鉴于水准网的线性化，采用间接平差最容易程序化实现。模型为［2］

将式（2）代入式（1），得

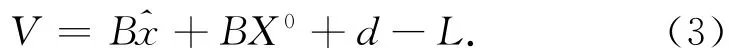
令l＝L－（BX0＋d），得误差方程为

由最小二乘原理BTPV＝0得＝（BTPB）－1BTPl，再代入式（2）、式（4）反求V，及。最后进行精度评定。但对于水准网观测值总能用所选参数线性表示，文献［3］指出在平差前可以不给出参数的近似值，简化后的模型为

将式（6）代入式（5），得

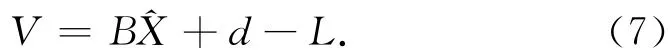
令l＝L－d，得误差方程为

由最小二乘原理BTPV＝0，得

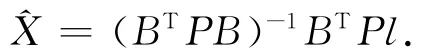
简化后的模型不需要求解参数的近似值，这种简化更易编程，平差结果直接为参数的估值。再代入式（6）、式（8）反求及V。

2 数据结构设计

合理的数据结构有助于程序编写效率的提高［4］。可以注意到对于任何网形，一条水准路线必然包括4个数据：起始点、高差、距离、终点，且H起＋h高差＝H终，因此在进行数据结构的设计中，必须体现出终点、起点，从而判断其与高差关系。定义已知点数据（见图1）字段为：序号、点号、高程。观测数据（见图2）文件字段为：测段序号、测段后视点名、测段前视点名、测段高差、测段距离。考虑到数据的可视化及编辑的人性化，数据的存储平台采用常规的.csv文件。

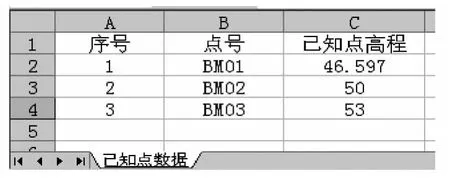
图1 已知点数据

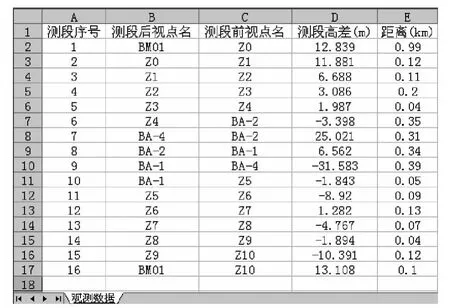
图2 观测数据

3 模型及程序实现

对于水准路线的追踪事实上就是对观测数据中“点名”的追踪；而间接平差模型中一个观测数据就对应一个方程，通过本文对数据结构的定义，我们从系数矩阵B就可以反映出任意网形。系数矩阵B及常数项自动形成的思想程序如图3所示。

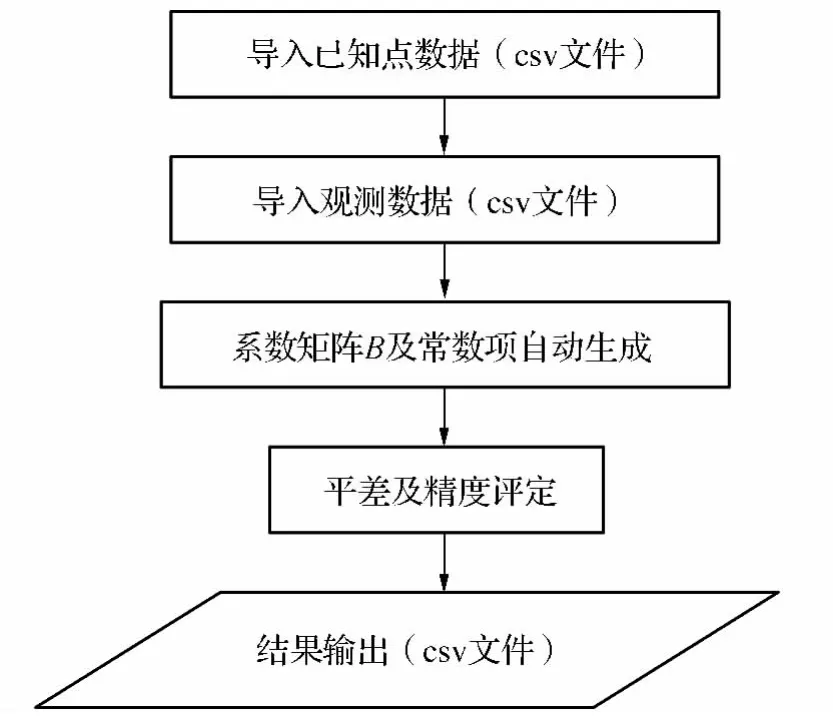
图3 流程图

for i＝1：cc2 %cc2－观测值个数

for j＝1：cc4 %cc4－未知点个数

移栽时注意不要碰散土坨，以防根系受伤。在地膜中间单行栽植，株距70厘米，每亩1100株左右，移栽完后及时浇透水，然后覆盖小拱棚，保证幼苗不受冻害。

if strcmp（name（j），nameB（i））＝＝1

B（i，j）＝－1；

end

if strcmp（name（j），nameF（i））＝＝1

B（i，j）＝1；

end

for j＝1：cc0%cc0－已知点个数

if strcmp（name0（j），nameB（i））＝＝1

B0（i）＝－str2num（H0｛j｝）；

end

if strcmp（name0（j），nameF（i））＝＝1

B0（i）＝str2num（H0｛j｝）；

end

end

Y0（i）＝str2num（YY｛i｝）；

s（i）＝str2num（ss｛i｝）；

end

4 工程应用及分析

电力行业，厂区范围一般不会很大。小的不到1km2，大的也不过2～3km2，而重点关注区域则更小，对水准控制要求的范围有限。结合工程实际，在满足规范要求的同时，也要考虑成本，力求经济适用。所以网形不会很复杂，路线也不会太长。实际操作中，只要依照规范进行，原始观测数据自然准确可靠［5］，后续的数据平差也就不需要考虑诸多不确定性的异常情况［6］。

已知数据文件见图1及图2，实例结果见表1及表2。

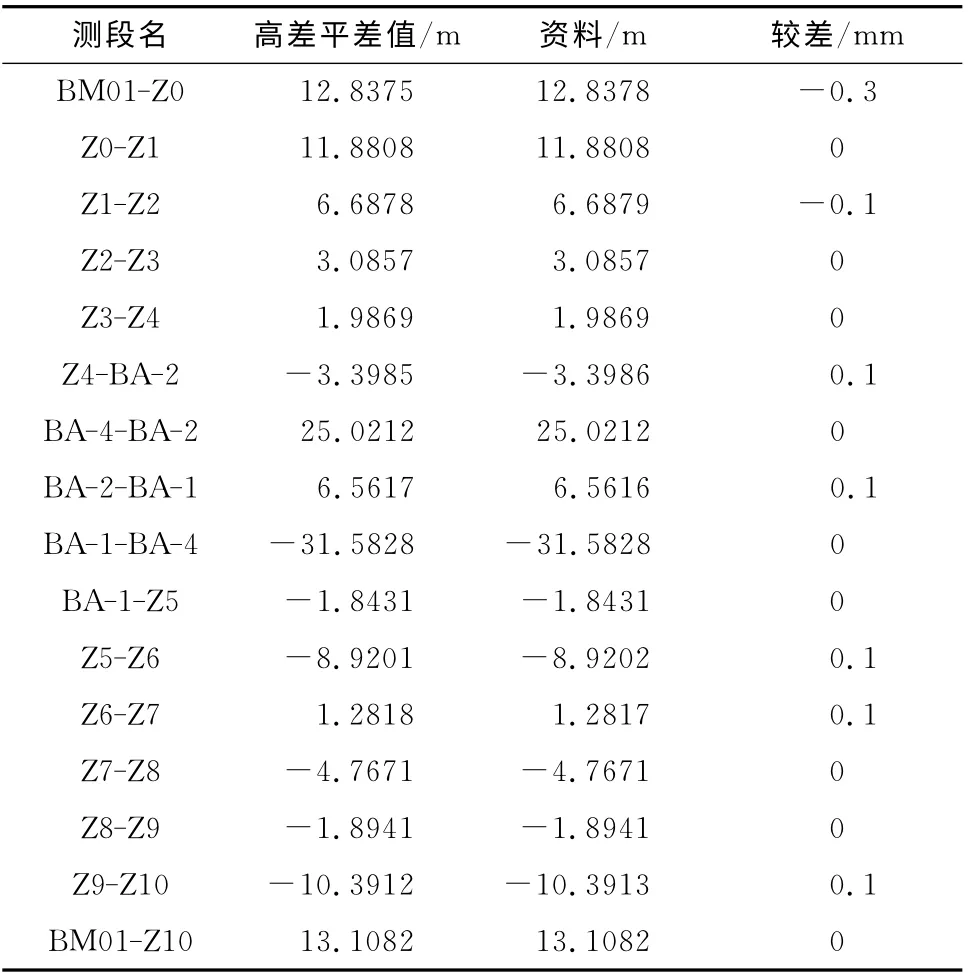
表1 高差平差值较差

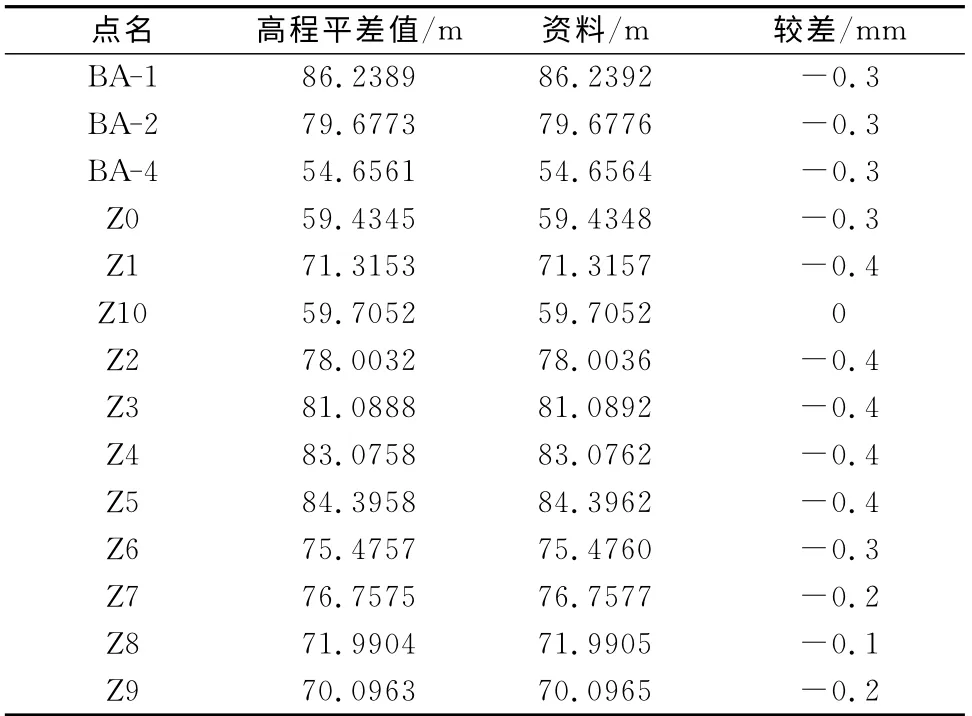
表2 高程平差值较差

对比分析：较差结果在亚毫米位，对于工程来讲是可以忽略的。可能会存在这样的疑问，高精度的变形监测允许的误差可能本身就要在亚毫米级，那么此处的较差就会被掩盖。这一点，需要作出解释，即：不同的程序实现方式从理论上也会出现这些细微的差别。在工程应用上，高精度的变形监测体现的是相对性，所用的平差程序自然是保持唯一性，不可能以多种软件混用所得到的结果来进行比较分析。那么在同一程序下运行时，亚毫米级的变化自然能得到体现，不会被掩盖。

5 结束语

间接平差理论是无可争议的成熟理论，本文在此基础上的程序实现，可以应用于任何等级的水准网平差。而在工程应用上，出现复杂网形及海量数据的情况基本可以排除，相应因素引起的不确定性当不用考虑。针对不同行业的作业模式，以此思维方式来进行数据的自动处理，经济适用，同时VC＋＋和MATLAB进行混合编程的方法已经实现，可以大大地减少源程序代码，缩短软件的开发周期［7－8］，值得推广。

［1］周建兴.Matlab从入门到精通［M］.北京：人民邮电出版社，2008.

［2］武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉：武汉大学出版社，2003.

［3］姚连璧，周小平.基于MATLAB的控制网平差程序设计［M］.上海：同济大学出版社，2006.

［4］王磊，谭志祥，张鲜妮，等.基于MATLA的水准网经典平差系统的开发和应用［J］.测绘科学，2010，35（5）：223－225.

［5］岑新远，范东明.粗差分类探测的选权迭代抗差估计方法［J］.测绘，2012（2）：51－53.

［6］李德仁，袁修孝.误差处理与可靠性理论［M］.武汉：武汉大学出版社，2002.

［7］柏晟.VC＋＋与MATLAB 6.5的混合编程方法研究与实现［J］.电脑开发与应用，2005（4）：24－27.

［8］陈东娇，刘庆繁，陈家焱，等.MATLAB 6.5与VC接口方法的研究［J］.机械与电子，2006（5）：9－11.