基于单CCD相机和经纬仪的几何测量方法研究

周满平，谭月胜

（北京林业大学 工学院，北京 100083）

随着以数字制造为核心的先进制造技术的快速发展，对精密测量技术的要求也越来越高。对物体几何的测量正向小尺寸测量和大尺寸测量两个不同的方向发展［1］。目前，大尺寸三维坐标测量的方法和系统主要有：三坐标测量机（CMM）、经纬测量系统（Theodolites）、全站仪测量系统（Total Station）、激光跟踪测量系统（Laser Tracker）、激光扫描测量系统（Laser Scanner）、关节式坐标测量机（Articulated Arms）、室内GPS（Indoor GPS）、工业数字摄影测量系统（Digital Photogrammetry）等［2］。

这些测量方式在一定程度上满足了生产、建设中的测量需求，但同时又有各自的不足之处。三坐标测量机具有高准确性、高效率、通用性好的特点，不足之处是属于接触式测量，不易对准特征点，并且对环境要求高、携带不方便；经纬仪测量系统具有光学、非接触并且测量准确度高的特点，但需要由两台或两台以上的高精度电子经纬仪来构成空间角度交汇测量，其两台经纬仪间的距离在每次移动后都需重新标定，影响精度，同时经纬仪测量系统需要逐点测量，测量速度慢、自动化程度不高；工业数字摄影测量具有高准确性、非接触和携带方便的特点，其原理为三角形交汇法，但需要在不同位置和方向拍摄同一物体两幅或以上的数字图像，与经纬仪类似，两台摄像机之间的距离在每次移动后都需重新标定，影响精度，并且价格较贵［2］。

结合经纬仪的测角功能和CCD相机的摄像功能，本文建立了一种新的视觉测量系统，该系统不仅具有经纬仪测量系统和工业数字摄影测量系统测量精度高、携带方便等优点［3－4］，还有效避免了测量过程中影响精度的因素，使用单CCD相机有效节省了成本。实验结果表明，基于单CCD相机和经纬仪的几何测量方法能够满足测量要求。

1 双目视觉原理测量系统

双目视觉原理就是双摄像机从不同角度同时获得目标物体的两幅数字图像，或者由一个摄像机在不同时刻从不同角度获取目标物体的两幅数字图像，基于视差得到物体的三维信息的原理［5－6］，如图1所示。

图1 双目视觉测量原理

图1中，O1，O2分别为两个摄像机的投影中心，O1O2为基线距B，B＝xO2－xO1，O1o1＝O2o2＝f为两个摄像机的焦距。

目标点P在图像坐标系中的坐标分别为P1（x1，y1），P2（x2，y2），其全局坐标系中的坐标待定，设为P（x，y，z）。

假定两摄像机的图像是在同一个平面上拍摄的，所以目标点P在两幅图像上的纵坐标相同，即y1＝y2。

由相似三角形原理可得

根据图1，设视差为D，则D＝x1－x2，并结合式（1）则可得到目标点P的三维坐标为

由以上可知，若已知目标点在两幅图像上的图像坐标P1（x1，y1，z1），P2（x2，y2，z2），以及两摄像机的焦距f、基线距B，即可得目标点的三维坐标信息。

2 基于单CCD相机和经纬仪测量原理

基于单CCD相机和经纬仪的测量系统的测量原理也是基于视差原理。由于CCD相机固定在经纬仪上，因此，CCD相机与经纬仪的相对位置固定不变。同时经纬仪的三角架固定，不再移动。只需转动经纬仪的水平角度就可以根据需要拍摄不同的数字图像，如图2所示。

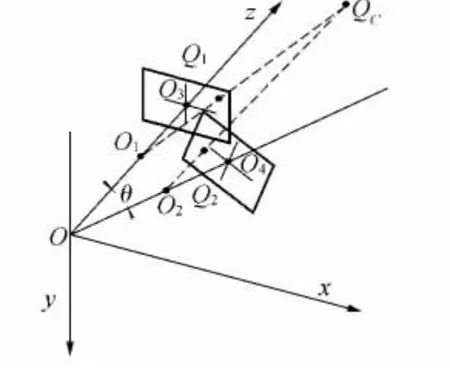
图2 基于单CCD相机和经纬仪测量原理

图2中O点为经纬仪坐标系原点，在此同时将其设定为空间坐标系的坐标原点，QC为目标点，坐标设为QC（xC，yC，zC），而Q1（x1，y1）和Q2（x2，y2）分别为目标点QC在两幅图像上的成像点。

OO1O3、OO2O4分别为从不同的角度拍摄时的位置，O1（xO1，yO1，zO1），O2（xO2，yO2，zO2）分别为两次摄影的投影中心。两个位置是由绕y轴转动θ角得到，x轴和z轴保持不变。投影中心到原点的距离为OO1＝OO2＝l，基线距为，因为是由同一相机在不同角度拍摄的图像，所以其焦距O1O3＝O2O4＝f。

2.1 基于单CCD测量的数学模型

由图2可知，O1的坐标为O1（0，0，l），O2（l×sinθ，0，l×cosθ），故可知基线距为

由式（2）可得

由式（3）知，若可获取摄影中心到原点的距离，即OO1＝OO2＝l，目标点分别在两幅图像上的成像点的坐标Q1（x1，y1），Q2（x2，y2）以及摄像机的焦距f，则就可通过式（3）获得目标点的三维坐标信息。

2.2 l，f的确定

由式（3）可知目标点三维坐标的求解过程，而由空间两点的距离公式可知：只要能够知道空间该两点（如Q1（x1，y2，z3），Q2（x2，y2，z3））的三维坐标，就可由距离公式求出两点的距离。也就是说如果能够知道两点的距离，那么就能够反求出l，f。设空间中存在4个点，分别为P1（xC1，yC1，zC1），P2（xC2，yC2，zC2），P3（xC3，yC3，zC3），P4（xC4，yC4，zC4）。

两点的距离公式为

所以P1，P2两点的距离为

所以P3，P4两点的距离为

将式（3）分别代入式（5）、式（6）可得方程组（7）。

由式（7）可知，要求得l，f就需要对4个目标点进行测量，每个目标点需要测量两次，所以一共需要测量8次，这样就可得到p1（x1，y1），p2（x2，y2），…，p8（x8，y8），以及转动的角度θ1，θ2，θ3，θ4，而同时a和b又是已知的，那么求解方程就可以得到l，f。

式中：

2.3 实验结果及分析

利用基于单CCD相机和经纬仪的测量系统对标定物进行测量。经纬仪为北京新北光BTD－2L系列中文激光电子经纬仪，该经纬仪使用了微型计算机技术能够实现测量自动计算、存储和显示等多功能，能够同时显示出水平角、垂直角测量结果数值，同时BTD－2L还配有RS－232C串行通信，可以将仪器观测值输入到计算机。CCD相机采用的是由加拿大PointGrey公司生产的FL2－14S3M－C，相片为黑白色，分辨率为1392×1040，帧/行频为17fps，像元尺寸为4.65μm，数据接口为1 394b。测量系统如图3所示。

图3 基于单CCD相机和经纬仪的几何测量系统

操作经纬仪和CCD瞄准标定物待测区域，获取经纬仪的角度信息及数字图像，并传输到计算机中。经纬仪绕y轴转动θ角（θ为能够保持待测量区域在图像中的任意角度），再一次瞄准标定物，获取经纬仪角度信息及数字图像，并传输到计算机中。运行计算机中的测量系统程序，计算出经纬仪的转动角度θ。两次不同角度的拍摄图像经MATLAB处理后结果如图4所示。

图4 MATLAB处理结果（左图为第一次拍摄图像，右图为转θ角后拍摄图像）

标定物格子边长为30mm的正方形。选取标定物中的4个目标点P1，P2，P3，P4，为方便计算，P1，P2和P3，P4为在同一线段上边的端点，由式（8）计算出l，f。由l，f及式（3）即可求出待测区域中任意点的三维坐标，本次实验测量的两点均为两条在同一直线边的端点，即实际距离为60mm。一共测量10组数据进行对比。对比内容包括实际数据、游标卡尺测量数据及本系统测量数据。对比结果如表1所示。

表1 测量数据对比 mm

由表1可以看出，无论是游标卡尺还是本系统的测量结果大部分要比实际尺寸要小，这是因为作为标定物的纸张在粘贴的时候发生了褶皱，导致尺寸变小。同时发现本系统测量结果与游标卡尺的测量结果最大误差为0.06mm，而游标卡尺精度为0.02mm，所以本系统精度为0.08mm。考虑到这个实验是标准标定物，其定位较容易，所以在其它测量中误差可能会有一定的增加。由实验结果可知，基于单CCD相机和经纬仪的测量系统能够满足测量要求。

3 结束语

本文首次提出一种综合CCD摄像功能及经纬仪测角功能的几何测量方法，该方法简单、易行，通过实验验证实验结果精度较高，可以应用在一般的几何尺寸的测量中，有一定的推广价值。

该系统中的经纬仪可以不限次数地转动，因此，该系统不仅可以用单CCD相机实现双目视觉原理，如果对测量程序进行改进还可以实现三CCD甚至多CCD的功能，这样可以对同一测量目标计算出多组数据平均值，以进一步提高精度。

［1］叶声华，王仲，曲兴华.精密测试技术展望［J］.中国机械工程，2000，11（3）：262－264.

［2］黄桂平，钦桂勤.大尺寸三坐标测量方法与系统［J］.宇航计测技术，2007，27（4）：15－19.

［3］邹剑，杨学友，林润芝，等.多站位CCD相机参数的标定方法研究［J］.传感器与微系统，2010，29（5）：44－56，52.

［4］孙长库，魏嵬，张效栋，等.CCD摄像机参数标定实验设计［J］.光电子技术与信息，2005，18（2）：43－46.

［5］张广军.机械视觉［M］.北京：科学出版社，2005.

［6］李德良，刘艳玉，张飞龙，等.双目视觉测径仪的单CCD实现［J］.军械工程学院学报，2007，19（5）：55－57，63.

［7］董秀山.图像边缘检测算法研究及应用［D］.哈尔滨：哈尔滨理工大学，2009.

［8］彭辉，文友先，吴兰兰，等.采用自适应canny算子的树上柑橘图像边缘检测［J］.计算机工程与应用，2011，47（9）：163－166.

［9］吕志伟，郝金明，许其凤，等.利用CCD数码相机进行高精度定位的方法［J］.测绘学院学报，2005，22（4）：242－245.

［10］冯仲科，赵英琨，邓向瑞，等.三维前方交会法测量树高及其精度分析［J］.北京林业大学学报，2007，29（2）：36－39.