基于滑动式Lagrange插值方法的GPS精密星历内插分析

雷 雨，赵丹宁，高玉平，2

（1.中国科学院国家授时中心，陕西 西安 710600；2.中国科学院时间频率基准重点实验室，陕西 西安 710600；3.中国科学院研究生院，北京 100039）

在高精度GPS定位导航与授时中，需要使用IGS（International GNSS Service）及数据分析中心提供的精密星历获取卫星坐标，但其采样间隔为15min和5min，而GPS接收机的采样率一般为30s、15s或5s，甚至更密。因此，若想利用某一时刻的卫星坐标，必须对精密星历进行高精度、快速的插值或拟合［1－2］。本文介绍了滑动Lagrange多项式插值方法的基本原理，以精密星历中固定采样间隔的卫星位置作为插值节点，对内插结果进行分析与讨论。

1 滑动Lagrange多项式插值

1.1 Lagrange多项式插值

经典的Lagrange插值函数为

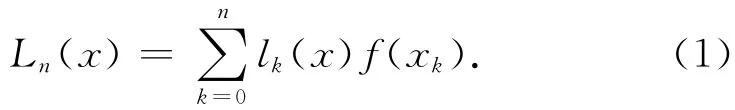
其中：f（xk）为插值节点处的函数值，lk（x）是n次插值基函数

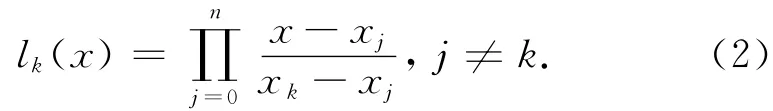
其仅与节点有关，不随函数值f（xk）的改变而改变。

插值点位于已知节点之间的称为内插。例如对于n阶插值，即有n＋1个插值节点，内插位于这n＋1个节点之间任意位置的函数值［3］。在进行多项式内插中，为了达到所需精度，常选择较高阶数的多项式，但随着阶数的增加，在插值端点的函数值易发生震荡或跳跃现象，即所谓的龙格现象（Runge's Phenomenon，RP）［4－5］。为了克服这个不足，多项式插值一般采用滑动式算法［6－7］。

1.2 滑动式内插算法

采用滑动式内插算法，就是使欲插值的点始终位于插值范围的中心，以获得最高精度的插值效果。例如，每次取8个插值节点，生成7阶多项式，最佳插值时间段处于第4个到第5个节点之间。第1个到第8个节点为第1个插值区间，仅用来插值第4个到第5个节点之间的时间段。这个插值区间相当于一个“窗口”，窗口大小一直保持不变，每次将窗口向后移动等间隔的距离，用于插值窗口中间两点之间的时间段。此外，窗口数据点的多少（多项式阶次大小）会对插值结果产生影响。需要说明的是，如果取偶数个节点，最佳插值时间段有2个。例如取9个插值节点，生成8阶多项式，最佳插值时间段分别处于第4个到第5个节点之间及第5个到第6个节点之间。研究表明，选取偶数个节点进行插值的效果优于奇数个节点［4，7－8］。

2 数值算例与分析

2.1 数值算例

为了验证内插结果，采用2011－06－27由IGS数据分析中心NGA发布的GPS卫星精密星历，选取PRN编号为02的GPS卫星的坐标值进行内插计算，时间段为00：00：00至08：25：00。精密星历的采样间隔为5min，为了验证内插精度，取15min间隔为一个节点，利用滑动式Lagrange方法内插出每5min间隔的卫星坐标，并与NGA提供的已知精密星历做比较。由于星历中边缘时刻的卫星位置需要利用相邻1d的数据才能内插得到，所以略去边缘时刻。表1给出了滑动Lagrange插值方法不同阶次的内插结果。

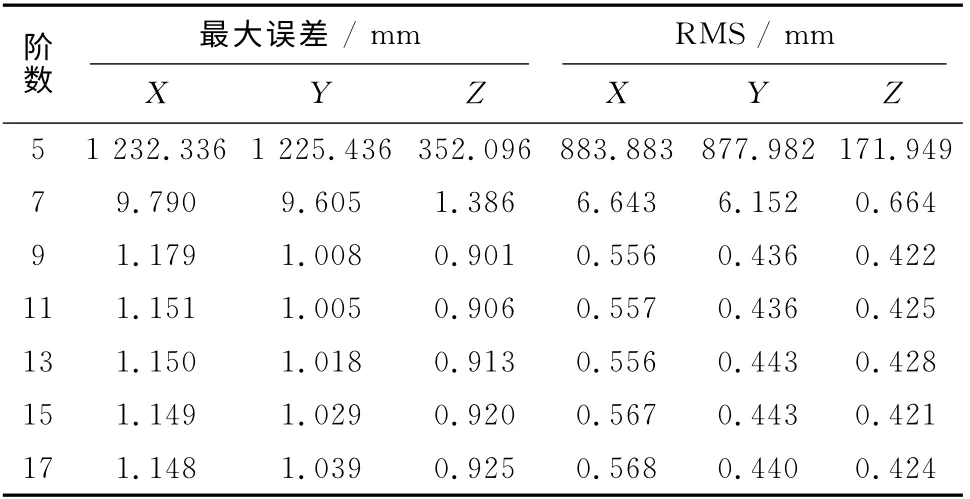
表1 不同阶次滑动式Lagrange内插结果

2.2 分析讨论

由表1可以看出，Lagrange多项式的阶数越高，内插精度也越高；当插值阶数在5阶以下时，Lagrange插值方法有较大误差，最大误差达到1m；当阶数在7阶时，已经达到了毫米的精度，当插值阶数超过9时，插值精度趋于平稳；另外，由于使用了滑动式内插算法，高阶次插值也没有出现龙格现象。

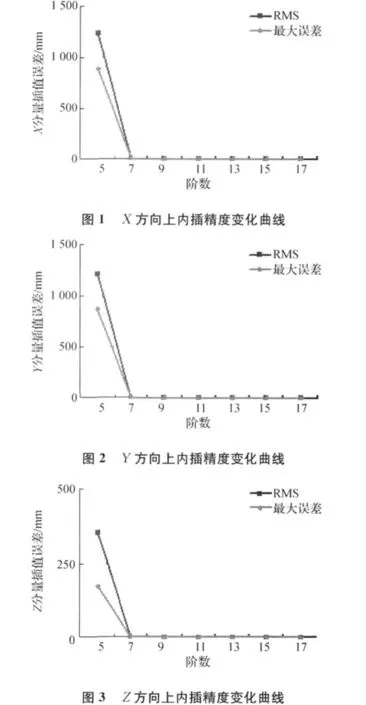
为了形象直观地表达插值精度的变化情况，图1、图2和图3分别给出X，Y，Z方向上Lagrange插值方法的最大误差和RMS变化曲线。

3 对GPS相位平滑伪距授时的影响

为了验证滑动式Lagrange插值算法的有效性，将7阶内插结果应用到基于非差载波相位平滑伪距的精密授时软件TCT中［9］。

选 择 了IGS/TAI并 址 站PTBB 2009－06－05（MJD＝54 987）的观测数据，采样率为30s，该站接收机外接H－maser频标。从IGS下载了对应时间的采样率为15min最终精密星历文件和采样率为30s的卫星钟差文件。将求解的接收机钟差序列与IGS对应的钟差求差，得到的序列偏差如图4所示，并统计了最大偏差（Max Bias）、平均偏差（Mean Bias）、均方差（RMS）和标准差（STD），见表2。

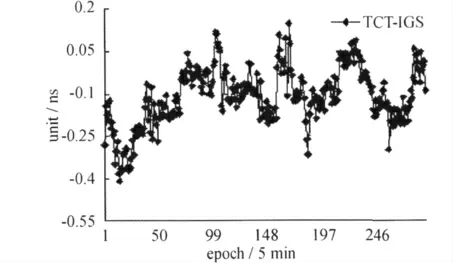
图4 求解钟差与IGS发布的钟差之间的较差

表2 接收机钟差解的精度统计信息 ns

从图4与表2中可以看出，利用上述精密星历处理方法的精密授时软件，进行双频载波相位平滑伪距单站授时时，其外符合精度可以保持在0.5ns以内，能满足高精度授时的需求。

4 结 论

1）对于采样率为15min的精密星历，采用滑动Lagrange多项式插值方法，当选取8个插值节点，即多项式阶次为7阶时，内插精度可以达到毫米级，完全可以满足高精度定位、定时等应用的需求；但随着插值阶次的增加，插值效果趋于平稳，因此，并不是插值阶次越高越好。

2）Lagrange插值方法的数学模型比较简单，属于代数插值，有利于计算机的编程实现，并且滑动式内值算法充分利用了待插时刻前后的数据信息，插值精度较高，即使插值阶次很高，也不会出现龙格现象。因此，在对GPS精密星历进行内插时，可以首选该方法。

3）将滑动式Lagrange插值算法应用到GPS相位平滑伪距授时软件中，取得了很好的效果，验证了其有效性。

［1］魏二虎，柴华.GPS精密星历插值方法的比较研究［J］.全球定位系统，2006，31（5）：13－15，20.

［2］洪樱，欧吉坤，彭碧波.GPS卫星精密星历和钟差三种内插方法的比较［J］.武汉大学学报：信息科学版，2006，31（6）：516－518，556.

［3］任锴，杨力.精密卫星钟差两种插值方法的比较［J］.测绘信息与工程，2009，34（6）：56.

［4］宫厚诚，李全海.基于IGS精密星历的卫星坐标和钟差插值［J］.全球定位系统，2009，34（5）：24－26，38.

［5］叶聪云，罗涛，陈远，等.精密卫星钟差的内插方法研究［J］.测绘信息与工程，2008，33（1）：11－13.

［6］邱蕾，廖远琴，花向红.基于IGS精密星历的卫星坐标插值［J］.测绘工程，2008，17（4）：15－18，14.

［7］张朋永，常青.GPS精密单点定位钟精密星历和钟差的内插算法选取［J］.测绘信息与工程，2010，35（2）：16－18.

［8］柳迪，逄淑涛，董绪荣.IGS精密星历文件的读取及内插方法研究［J］.全球定位系统，2011，36（5）：46－48，64.

［9］雷雨.GPS载波相位时间比对数据处理［D］.西安：中国科学院国家授时中心，2010.