柴油机缸套表面微沟槽织构润滑性能仿真分析
尹必峰 钱晏强 李晓东 刘胜吉 符永宏
江苏大学,镇江,212013
0 引言
当前,节能、减排、高效的发展趋势对发动机摩擦副,尤其是缸套-活塞环关键摩擦副提出了更为严格的要求:一方面需要降低燃油消耗,减小摩擦损失,提高润滑性能;另一方面,按照发动机日趋严格的排放要求尤其是颗粒排放要求,需要严格控制和降低机油消耗。改善发动机的润滑性能与控制机油消耗是一对矛盾,因此,在满足高性能的现代发动机缸套-活塞环摩擦磨损与可靠性要求、保证良好润滑性能的同时,实现机油消耗与排放的有效控制,是当前发动机摩擦学研究的关键问题。缸套表面的传统平台珩磨技术可以增大其表面的实际承载面积,增大摩擦表面承载力,而且珩磨痕迹形成的网状微沟槽有利于形成储油单元,这对降低机油消耗都有一定的作用,但由于传统的平台珩磨所采用的油石磨粒的不均匀性和珩磨过程中的多个随机性因素,从而使得加工的不均匀性较大,加工出的珩磨网纹微沟槽的分布深浅不一,沟谷宽窄不等,轨迹纹路紊乱无序。近年来,随着激光加工技术的不断发展和成熟,激光表面织构技术以其独特的加工速度快、可控性强、加工精度高、零污染等优势,成为最成功的表面织构加工技术之一[1],这为缸套-活塞环表面的主动优化设计提供了技术基础。
国内外学者都对缸套-活塞环摩擦副表面织构比较关注。Ronen等[2]首先建立了简化的流体动压润滑模型,采用Reynolds空化边界条件和有限差分法,通过求解雷诺方程,证实了表面织构在流体润滑的情况下可以产生油膜压力,并且通过对表面织构的尺寸、深度和单元面积占有率的优化,有效改善了缸套-活塞环的润滑情况。Sadeghi等[3]针对缸套及活塞环表面微造型,引入了流体润滑与弹性流体润滑计算模型,分析了发动机上止点处不同微造型深度下弹性接触的承载力变化及摩擦力的变化情况,研究得出:微凹腔深度对于表面接触行为起着至关重要的作用,当深度太大时,反而不利于改善润滑情况。Etsion等[4]对部分织构活塞环对柴油机燃油消耗及排放性能的影响进行了试验研究,结果表明:装配部分织构活塞环的发动机,燃油消耗可以降低4%左右,排放性能及烟度略有改善。符永宏等[5]建立了微凹腔造型缸套及活塞环表面流体润滑理论模型,并利用变异的多重网格法进行求解,分析了缸套表面微凹腔半径、面积占有率、深径比等参数对润滑油膜厚度以及平均摩擦力的影响。王晓雷等[6]在SiC陶瓷表面加工表面织构,利用试验证实了表面织构能够有效提高摩擦副表面的润滑油承载能力。
以上研究为实现表面织构与发动机性能的优化匹配提供了必要的理论依据,但这些研究并没有考虑表面织构对混合润滑区域的影响,也没有考虑表面粗糙度对流量因子的影响,这使得理论模型在一定程度上不能够真实地反映缸套-活塞环的摩擦学性能,并且以上研究都是针对离散的微凹腔织构的润滑性能模拟,而对连续的微沟槽织构的润滑性能及相关参数的优化设计都缺少充足的理论研究。为了更真实地模拟缸套-活塞环的实际工作情况和探索微沟槽织构的润滑性能,本文建立了基于混合模型的缸套表面微沟槽织构的数学模型,分析了微沟槽形貌参数对摩擦副润滑性能的影响规律。
1 数学模型的建立
1.1 几何模型
活塞环为矩形环,忽略缸套的曲率半径,将缸套展开成平面(图1a),假设微沟槽在缸套表面均匀分布,取一个假想的边长为L的正方形控制单元,其中包含一条微沟槽(图1b),微沟槽表面积与正方形控制单元面积之比定义为微沟槽的面积占有率Sp,微沟槽宽度为w,c(t)为最小油膜厚度,微沟槽与活塞运动方向夹角为α,微沟槽深度为hp,深宽比为e=hp/w。
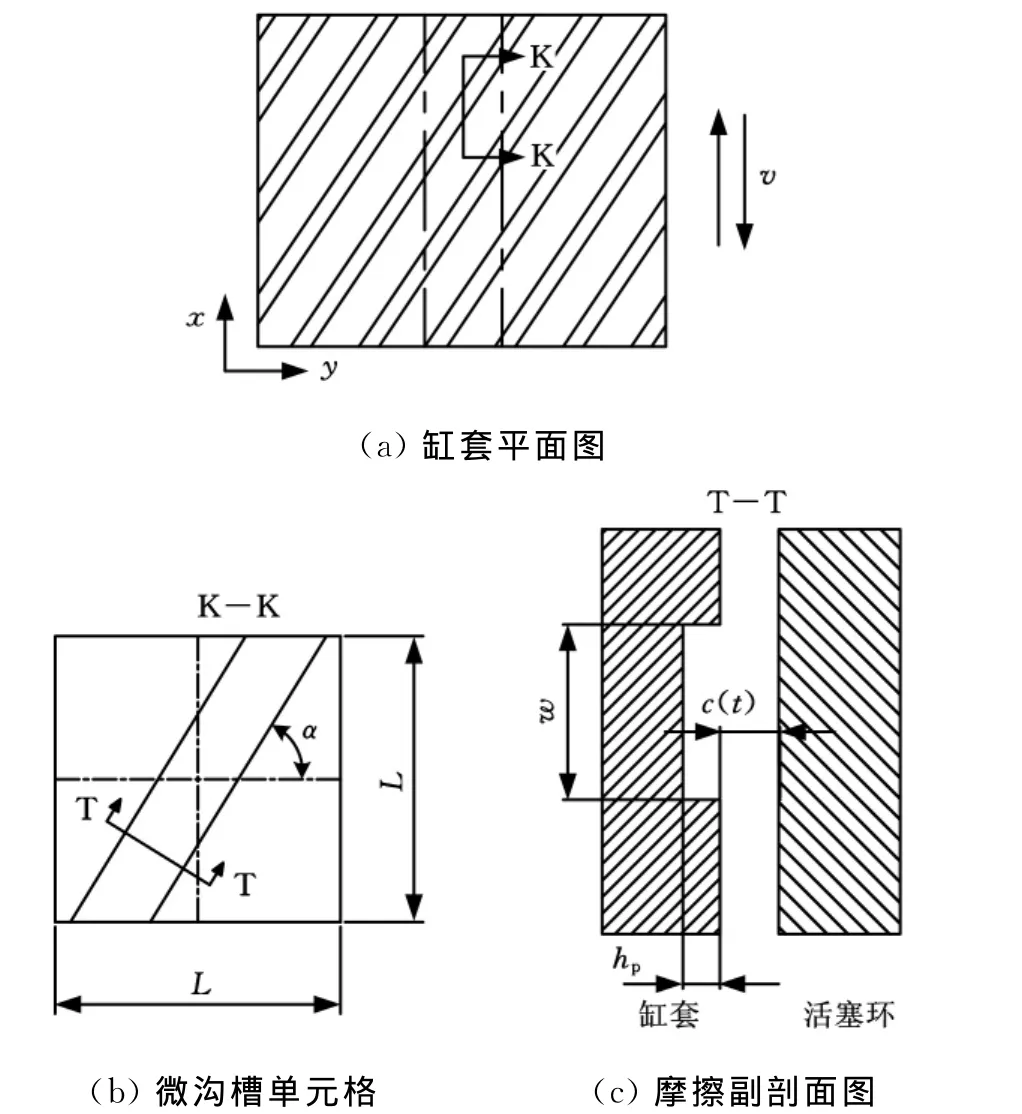
图1 微沟槽几何模型
1.2 雷诺方程
在建立缸套-活塞环润滑理论模型之前作以下假设:①活塞环被润滑油充分润滑;② 润滑油是不可压缩流体,其密度不随压力变化;③活塞环、缸套属于刚性体,即两者表面始终平行;④由于润滑油膜厚度很小,可以认为润滑油膜膜压沿膜厚方向保持不变。
由以上假设并借鉴Patir等[7]提出的方法添加压力和剪切流量因子来考虑润滑表面粗糙度对润滑性能的影响,得到不可压缩流体等温条件下的雷诺方程:


1.3 微凸体接触方程
本文采用Rohde[8]建立的粗糙度接触模型来研究微凸体的相互接触行为。粗糙表面微凸体间的接触力和粗糙表面的实际接触面积的表达式分别为


式中,WA为总的粗糙表面微凸体接触力;Ac为粗糙表面实际接触面积;A为粗糙表面名义接触面积;λ、β分别为微凸体密度和曲率半径;F1(H)、F2(H)为关于H 的函数;E′为两表面综合弹性模量;H为膜厚比。
1.4 油膜厚度方程
缸套表面任意点的名义油膜厚度为

式中,Ω为缸套表面所有微沟槽的区域集合;h(x,y,t)为任意位置膜厚。
实际油膜厚度为

式中,δ1、δ2分别为缸套、活塞环润滑非织构区域表面的随机粗糙峰元高度。
将膜厚比H定义为名义油膜厚度与综合粗糙度的比值,其表达式为

以膜厚比H为标准判断润滑状态:当H>4时为流体动压润滑;当H<4时为混合润滑。
1.5 摩擦力求解方程
在混合润滑状态下,摩擦力F由峰元摩擦力FA和流体摩擦力FH组成,即
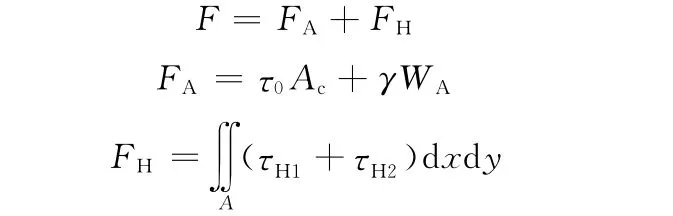
式中,τ0为剪切应力常数;γ为比例系数,由材料决定;τH1、τH2分别为流体间的剪应力和流体作用在峰元上的水平力。
2 数值计算结果分析
为了改善计算过程的数值稳定性,对以上方程进行量纲一处理,并采用有限差分方法离散偏微分方程,利用MATLAB编程求解。本文以某车用轻型柴油机为对象,其标定功率为68kW,标定转速为3200r/min,以实测的示功图(缸压)计算活塞环背压,在标定工况点进行数值计算。
2.1 混合模型中油膜压力与微凸体压力
图2所示为 w=60μm,hp=4.8μm,Sp=0.15,微沟槽角度α=60°时混合模型中量纲一油膜压力p与微凸体压力pA变化曲线。可以看出,通过缸套表面微织构造型,在发动机行程大部分区域由微沟槽产生的流体动压力支撑外载荷,微凸体压力仅在曲轴转角αc为0°(上下止点)附近出现,在上止点处达到最大。在上止点处活塞速度为0,油膜压力由挤压效应产生,造型区域的油膜所产生的流体动压润滑效应较弱,油膜压力仅占整个外载荷的13.6%,此时微凸体接触力主要起平衡外载荷的作用。但是通过表面织构,仍可以在上下止点处产生一定的油膜压力,这有利于改善摩擦面的润滑性能。
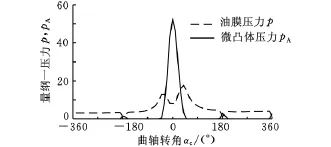
图2 混合模型中量纲一油膜压力与微凸体压力变化曲线
图3为 w=60μm,hp=4.8μm,Sp=0.15,α=60°时混合模型中上止点处量纲一油膜压力的三维图与二维图。可以看出,在上止点处,表面织构微沟槽仍然可以产生峰值约为16的量纲一油膜压力,可以有效地改善润滑状态,并且挤压效应可形成两个以微沟槽为轴的对称压力区域。

图3 上止点处油膜压力三维图与二维图
2.2 微沟槽与活塞运动方向的夹角的影响
图4所示为 w=60μm,hp=4.8μm,Sp=0.25,微沟槽角度α不同时,最小膜厚比Hm的变化曲线。随着α的增大,最小膜厚比逐渐增大,当α达到60°之后,最小膜厚比的变化渐趋平缓。这主要是因为微沟槽所形成的储油单元随微沟槽角度的增大对润滑油的阻滞作用越明显,润滑油在织构区可以形成有效的动压润滑油膜,从而增强动压润滑效果。反之,当微沟槽角度较小时,润滑油的流动性较强,难以在织构区起到动压润滑作用。
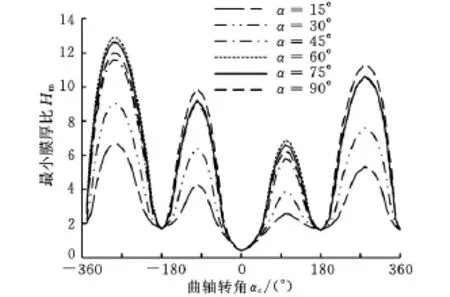
图4 微沟槽角度不同时最小膜厚比变化曲线
图5所示为 w=60μm,hp=4.8μm,Sp=0.25,微沟槽角度α不同时,量纲一摩擦力F的变化曲线。可以看出,随着微沟槽角度的增大,量纲一摩擦力相应减小。同上所述,当微沟槽角度增大时,润滑油的阻滞作用增强,从而有效地增强了动压润滑,使得油膜厚度增大,量纲一摩擦力减小。并且可以看出,当微沟槽角度为60°和90°时,润滑效果最好。

图5 微沟槽角度不同时量纲一摩擦力变化曲线
图6、图7分别为 w=60μm,hp=4.8μm,Sp=0.25,曲轴转角αc=-270°,微沟槽角度α不同时,量纲一油膜压力的三维图与二维图。可以看出,随着微沟槽角度的增大,油膜压力峰值不断增大,而且油膜压力的分布范围也随之变化。这主要是由于微沟槽角度较大时,对润滑油流动阻力较强,从而可以产生较大的油膜压力,在织构区附近形成良好的动压润滑油膜。但是微沟槽角度不仅对该摩擦副的润滑摩擦性能影响很大,对发动机机油消耗影响也很大,当微沟槽角度太大时,会影响油膜的均匀性,不利于润滑油的流动,影响油环刮油效果,造成机油消耗增加和排放超标。因此,综合考虑润滑性能与机油消耗,选取60°为最佳微沟槽角度。

图6 微沟槽角度不同时量纲一油膜压力三维图
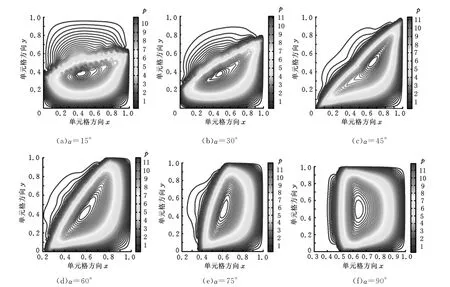
图7 微沟槽角度不同时量纲一油膜压力二维图
2.3 微沟槽面积占有率Sp的影响
图8所示为w=60μm,hp=4.8μm,α=60°,微沟槽面积占有率Sp不同时最小膜厚比Hm的变化曲线。可以看出,在上下止点附近由于活塞运动速度较低,油膜产生的流体动压润滑效应较弱,此时的油膜压力主要由时变效应产生,所以最小膜厚比相对较低,且不同的微沟槽面积占有率对其影响不大。当在各冲程中部,活塞运动速度较高,Sp>0.15时,最小油膜厚度随微沟槽面积占有率增大而减小,而且随着活塞运动速度增大,差异性表现得尤为明显。

图8 微沟槽面积占有率不同时最小膜厚比变化曲线
图9所示为w=60μm,hp=4.8μm,α=60°,微沟槽面积占有率Sp不同时,量纲一摩擦力F的变化曲线。可以看出,在上止点附近,微沟槽面积占有率变化对量纲一摩擦力影响较大,在其他区域面积占有率对摩擦力影响不大,且在做功行程的上止点附近,由于油膜厚度较小且气缸压力较大,故摩擦力达到最大值,活塞工作环境也最为恶劣。随着微沟槽面积占有率的增大,在一定区域中处于微沟槽区域的比例会增大,造成该区域的油膜厚度增大,摩擦力减小,这就造成了混合区域平均摩擦力的减小,当Sp从0.1增大到0.4时,平均量纲一摩擦力减小了14.9%。当Sp=0.15时,量纲一摩擦力值最小。综合考虑,选取0.15为最佳的面积占有率。
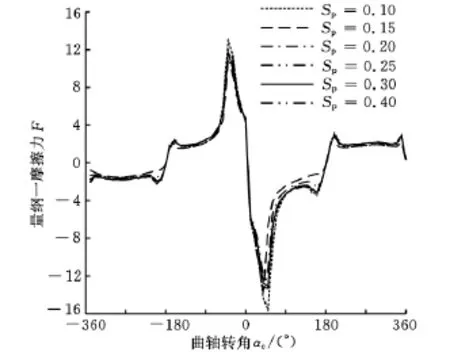
图9 面积占有率不同时量纲一摩擦力变化曲线
2.4 微沟槽深宽比e的影响
图10所示为w=60μm,Sp=0.25,α=60°,微沟槽深宽比e不同时最小膜厚比变化曲线。微沟槽深宽比对最小膜厚比影响较大,在各行程中部,由于活塞运动速度较高,动压润滑效应较为明显,所以不同深宽比对最小膜厚比产生的影响更为明显。当e=0.200时,微沟槽深度过大,动压润滑效应不明显,故最小膜厚比较小且变化幅度不大,几乎整个行程的最小膜厚比都小于4,即处于混合润滑状态。当e=0.025时,微沟槽深度过小,不能有效形成良好的润滑油膜,其载荷平衡主要通过油膜的挤压来实现,故其油膜压力将过大。在各个行程中,当e≥0.050时,最小膜厚比随深宽比增大而减小;当e从0.050增大到0.200时,最小膜厚比减小了64%左右;当e从0.025增大到0.050时,最小膜厚比增大了10%左右。

图10 深宽比不同时的最小膜厚比变化曲线
图11所示为w=60μm,Sp=0.25,α=60°,微沟槽深宽比e不同时量纲一摩擦力变化曲线。可以看出,随着微沟槽深度的增大,量纲一摩擦力不断增大。但是当e较大时,动压润滑效果较差,油膜产生的油膜压力较小,导致摩擦状况恶劣。当e从0.025增大到0.150时,平均量纲一摩擦力增大了2.3倍左右,可见微沟槽深度不宜过大。当hp取3~5μm之间时,活塞环-缸套摩擦副的润滑性能较佳。
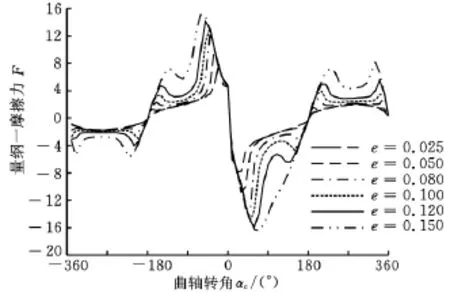
图11 深宽比不同时量纲一摩擦力的变化曲线
3 结论
(1)本文在考虑了缸套表面粗糙度的情况下,建立了缸套表面微沟槽织构的混合润滑理论模型,更加真实地反映了活塞环-缸套摩擦副的摩擦学性能。同时通过理论计算给出了微沟槽织构的理论优化参数,为实现微沟槽织构的主动优化设计提供了理论依据。
(2)分析了微沟槽表面织构混合润滑模型的摩擦性能,通过缸套表面织构造型,微沟槽可以在发动机大部分行程阶段产生动压润滑油膜压力,摩擦副处于流体润滑状态;在上下止点附近非造型区域的粗糙表面与活塞环表面相互接触,摩擦副处于混合润滑,微凸体作用力起平衡外载荷的主要作用;但是通过表面织构,仍可起到一定的改善润滑的作用。
(3)混合模型中微沟槽角度(与活塞运动方向夹角)过小时,润滑油流动性较好,不利于形成良好的润滑油膜;微沟槽角度过大时,微沟槽对润滑油的截流阻力较大,不利于油环的刮油效果,综合考虑机油消耗性能,得出最佳微沟槽角度为60°左右。面积占有率仅在上止点附近对量纲一摩擦力有较大影响,在其他区域面积则影响较小,但仍可得出面积占有率Sp=0.15左右时最佳。微沟槽深宽比对摩擦副润滑性能较大,随着微沟槽深度的增大,量纲一摩擦力不断增大,且当微沟槽深度较大时,润滑效果不明显,当hp取3~5μm之间时,活塞环-缸套摩擦副的润滑性能较佳。
[1]华希俊,符永宏,王霄,等.内燃机缸套激光珩磨技术及其能试验研究[J].中国机械工程,2007,18(24):2989-2992.Hua Xijun,Fu Yonghong,Wang Xiao,et al.Experimental Research on Laser Honing of Engine Cylinder Bore[J].China Mechanical Engineering,2007,18(24):2989-2992.
[2]Ronen A,Etsion I,Kligerman Y.Friction-reducing Surface-texturing in Reciprocating Automotive Components[J].Tribol.Trans.,2001,44(3):359-366.
[3]Sadeghi F,Wang C P.Advanced Natural Gas Reciprocating Engine:Parasitic Loss Control Through Surface Modification[R].Cambridge:Mechanical Engineering Tribology Laboratory,2005.
[4]Etsion I,Sher E.Improving Fuel Efficiency with Laser Surface Textured Piston Rings[J].Tribology International,2009,42(4):542-547.
[5]符永宏,陆华才,华希俊,等.激光微珩磨缸套润滑耐磨性能理论分析[J].内燃机学报,2006,24(6):559-564.Fu Yonghong,Lu Huacai,Hua Xijun.Theoretical Analysis on Lubrication and Wear-resisting of the Honed Cylinder Liner[J].Transactions of Csice,2006,24(6):559-564.
[6]王晓雷,韩文非,加藤康司.碳化硅陶瓷的水润滑特性及其表面微细织构的优化设计[J].中国机械工程,2008,19(4):457-460.Wang Xiaolei,Han Wenfei,Kato Koji.Surface Texture Optimal Design for Silicon Carbide under Water Lubrication[J].China Mechanical Engineering,2008,19(4):457-460.
[7]Patir N,Cheng H S.An Average Flow Model for Determining Effects of Three-dimensional Roughness on Partial Hydrodynamic Lubrication[J].Trans.ASME,1978,100:12-18.
[8]Rohde S M.A Mixed Friction Model for Dynamically Loaded Contacts with Application to Piston Ring Lubrication[C]//Proc.of the 7th Leeds-Lyon Symposium on Tribology.Lyon,1980:262-278.

