电动轮自卸车动力总成悬置系统分析与优化

尹 庆 谷正气，2 陶 坚 伍文广 徐 亚

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

2.湖南工业大学，株洲，412008

0 引言

汽车动力总成悬置系统连接动力总成和车架，主要承受动力总成重量及隔离发动机与车架振动传递，因此动力总成悬置系统对汽车NVH（Noise，Vibration and Harshness）性能及驾驶员乘坐舒适性有很大影响［1］。合理匹配动力总成悬置系统，研制开发先进悬置部件，成为控制动力总成悬置系统振动和噪声的重要任务之一［2］。电动轮自卸车动力总成的质量很大且难以减小，发动机扭矩和冲击均较大，使得动力总成对车身的振动激励相对增加。可以通过对动力总成悬置安装位置、安装角度和各向刚度等进行优化设计［3-4］来改善电动轮自卸车整车振动及噪声水平。

本文建立了电动轮自卸车动力总成悬置系统六自由度模型，运用优化拉丁方法，计算分析对电动轮自卸车动力总成悬置系统解耦布置影响较大的悬置静刚度参数，将这些参数作为主要设计参数结合遗传算法与模拟退火法进行确定性优化；然后采用Monte Carlo方法分析悬置主刚度具有很大离散性时系统解耦程度的分布和系统解耦程度对悬置主刚度变化的灵敏度，以检验优化结果的稳健性，保证设计思想在实际生产中的可行性。

1 动力总成悬置系统动力学模型

目前电动轮自卸车的传动方式主要为交-直流传动，由柴油发动机带动发电机发电，经外部整流装置整流变成直流电输往汽车后桥两侧的直流牵引电机以驱动汽车行驶［5］。发电机与柴油发动机一起安装在动力总成底架上构成动力总成，其三维模型如图1所示。

图1 动力总成三维模型

由于动力总成固有频率远大于悬置系统频率，故将动力总成视为刚体，动力总成悬置系统可简化为一个空间六自由度振动系统，如图2所示。

图2 动力总成悬置系统

图2中，OXYZ为动力总成质心坐标系，O为动力总成质心，X轴平行于发动机曲轴轴线指向发动机前端，Z轴垂直曲轴向上，坐标系遵循右手定则。悬置布置方法为四点式悬置平置布置。图2中，1、2、3、4为悬置的布置点，1为左前悬置，2为左后悬置，3为右后悬置，4为右前悬置。悬置系统中每个悬置简化为沿其三个弹性主轴方向具有刚度和阻尼的元件［6］，各悬置弹性主轴方向U、V、W 与动力总成质心坐标X、Y、Z方向一致。

广义坐标为动力总成质心沿X、Y、Z轴的平移x、y、z及绕X、Y、Z轴的转角θx、θy、θz，即X＝（x，y，z，θx，θy，θz）T。利用拉格朗日方程推导出系统的振动微分方程为

式中，M为系统的质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵；f（t）为系统所受的激振力。

不考虑阻尼和外力作用，可得到系统自由振动的微分方程，即系统六自由度固有特性的分析方程为

2 原始模型分析计算

2.1 能量解耦法

动力总成悬置系统的质量矩阵和刚度矩阵通常存在很多非零元素，即系统存在惯性耦合和弹性耦合，因此需要对系统进行振动耦合分析。能量解耦法仅需对系统进行自由振动分析求得刚体模态参数，具有普遍的实用性。从能量角度来看，耦合就是沿某个广义坐标方向的力（力矩）所做的功转化为系统沿多个广义坐标的动能和势能。系统沿某个广义坐标振动的动能和势能可以相互转换，但其总和不变，故系统沿某一个广义坐标的总能量可用最大动能（或势能）表示。

当系统以第j阶模态振动时，第k个广义坐标分配的能量Ek，ωj占系统总能量Eωj的百分比为

Pjk的大小代表解耦程度的高低，若其值为100%，则系统做第j阶模态振动时能量全集中在第k个广义坐标，此时振型矩阵φ中第j列第j行的非对角元素φjj全为零，即第j阶模态振动完全解耦［7］。

2.2 模型原始数据

现有某电动轮自卸车动力总成悬置系统，其质量m及转动惯量参数如下：

各悬置的位置参数及刚度参数如表1和表2所示，其中坐标原点位于动力总成质心处。

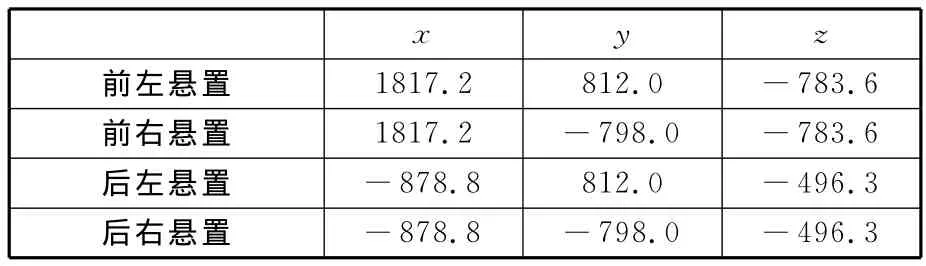
表1 悬置位置参数 mm

表2 悬置刚度参数 N／mm

2.3 系统振动特性分析

根据以上分析，用MATLAB语言编写计算程序求得动力总成悬置系统的固有频率和各方向能量分布，如表3所示。由表3可以看出，系统的1阶固有频率为4.38Hz，数值偏低；系统固有频率分布比较密集，配置不够合理，需要进行调整。从解耦率角度来看，原悬置系统除y方向和θx方向能量分布接近90%外，其余各向自由度解耦程度不高，能量分布均小于66%，z方向和θx方向的振动与其他方向的振动仍存在一定程度的耦合，这将不利于隔振设计，有必要对原悬置系统的解耦率进行优化。

表3 优化前总成悬置系统固有频率和能量分布

3 悬置系统优化设计

3.1 建立目标函数

动力总成悬置系统能量法解耦就是使系统在某一共振频率下，某一广义坐标方向的能量占优程度尽可能高，同时要满足悬置系统的模态频率分布与位移控制等约束条件。因此整个系统满足约束条件的优化目标为

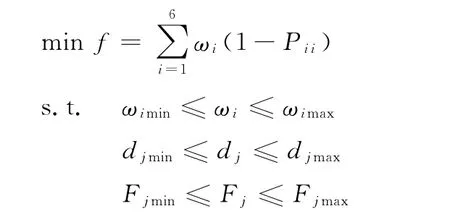
式中，ωi为系统第i阶固有频率；dj为动力总成重力工况下第j个悬置点位移；Fj为动力总成重力工况下第j个悬置点受力，j＝1，2，3，4。

3.2 约束条件和设计变量

动力总成的位置受到车架等构件的限制，悬置的角度、位置可变动的范围很小［11］，这里选取悬置各项刚度值为优化参数，共12个变量。

3.3 实验设计分析

通过实验设计（design of experiment，DOE）可以系统有效地分析设计空间，评估设计变量对目标函数和约束的影响，对设计变量进行敏感度分析，从而对设计参数进行筛选，减小问题的规模。实验设计方法主要有全因子法、参数实验、正交数组法、中心复合法、拉丁方法和优化拉丁方法［12］。

优化拉丁方法的基本思想是将每个设计参数的设计空间均匀地划分为边长为N的方阵，然后在方阵中随机取得不同行不同列的N个采样点。该方法采样点比较均匀，可获得充分的模型信息，故本文选用优化拉丁方法。

根据优化拉丁方法确定的30个实验设计方案进行计算分析，得出设计变量对目标函数的影响关系，如图 3 所示。图中，Klfx、Klfy、Klfz、Krfx、Krfy、Krfz分别表示左前悬和右前悬x、y、z三个方向的刚度参数；Klrx、Klry、Klrz、Krrx、Krry、Krrz分别表示左后悬和右后悬x、y、z三个方向的刚度参数。

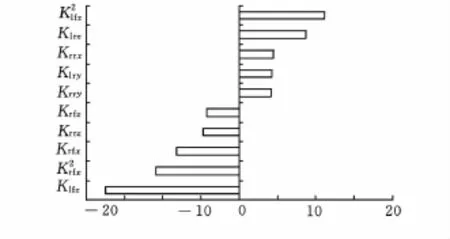
图3 刚度参数Pareto图

由图3可以看出，对该动力总成悬置系统解耦布置影响最大的变量为Klfz，目标函数随着Klfz的增大而减小，同时K2lfz对目标函数影响也很大，但是随着其值的增大目标函数呈增大趋势；Klrz、Krfx对目标函数的影响也相对较大。

3.4 优化设计

近年来国内一些学者将遗传算法应用于动力总成悬置系统解耦分析中，取得了良好的效果［10］。遗传算法具有鲁棒性强、适于并行处理及高效应用等特点，但遗传算法本身仍存在很多缺陷，如在实际应用中容易产生早熟收敛的问题，而且在进化后期搜索效率较低等。

模拟退火算法也是一种近年来兴起的一种性能较好的寻优方法，该方法可以接受劣质解，具有很强的局部搜索能力，一般能够得到全局最优解，但它对参数依赖性强，需要足够的降温和充分迭代次数来保证其全局收敛性。针对遗传算法容易陷入早熟收敛而模拟退火算法可以接受劣质解从而跳出局部最优的特点，将两种算法结合应用到动力总成悬置系统优化问题中，以克服两种算法各自的不足［13-14］。

算法的设计步骤如下：

（1）给定算法参数。初始种群规模为N，初始温度为T0，交叉概率为Pc，变异概率为Pm。

（2）初始化种群。

（3）在当前温度Tk下，计算初始种群适应度值。

（4）对种群中的染色体执行带最有保留策略的选择操作，然后进行基于“树”的交叉操作与变异操作。

（5）在当前解邻域内产生有微小变动的新解，按照SA的Metropolis准则接受新解。

（6）判断是否达到种群规模，达到则进入下一步，否则返回第（4）步。

（7）判断是否达到指定进化代数，输出结果，结束；否则退温，返回第（3）步。

这里取初始种群规模为100，运算100次时算法终止，T0＝2500，Pc＝0.8，Pm＝0.01。利用MATLAB编程优化计算悬置系统的频率与能量分布。考虑工程实际需要，悬置各项刚度取整，结果如表4所示。优化后动力总成悬置系统固有频率和能量分布如表5所示。比较表3和表5可知，系统的6个固有频率都集中在5～15Hz之间，满足频率约束条件。同时，对振动影响较大的z向平动自由度上的解耦率从46.49%提高到了99.73%，绕曲轴轴线旋转方向θx上的解耦率从87.74%提高到了92.24%，其他自由度上的解耦率也都有很大提高。

表5 优化后动力总成悬置系统固有频率和能量分布

3.5 计算模型的验证

为验证计算程序的正确性，应用机械系统动力学仿真分析软件（ADAMS）对发动机的悬置系统进行仿真计算。对模型各元件赋值后，利用ADAMS的振动分析求解器，可以求得优化后系统六阶固有频率及各阶频率中的能量分布，结果如表6所示。

表6 优化后由ADAMS计算的动力总成悬置系统固有频率和能量分布

对比表5和表6可以看到，两种方法计算得到的固有频率基本相等，能量分布矩阵基本一致，两者差值很小，最大结果误差仅为0.86%。

4 悬置系统稳健性分析

Monte Carlo法是一种随机模拟或统计实验法，它采用随机生成方法模拟真实系统的功能和发展规律，从而达到揭示系统运行规律的目的，它实际上是通过随机变量的统计实验和随机模拟来求解数学、物理和工程技术问题近似解的数值方法［15］。

实际生产中悬置的主刚度在一个较大的范围内波动，很难从工艺上保证上述优化计算值的精确度，因此降低软垫主刚度的变化对于系统解耦程度的影响是一个实际中必须解决的问题。本文根据部分样品实测的结果，假定动力总成悬置的主刚度满足正态分布，标准差为10%，对优化前后的悬置系统进行稳健性分析。分别经过1000次随机实验分析，优化前结果如图4、图5所示，优化后结果如图6、图7所示。

图4 优化前垂直方向模态能量分布概率

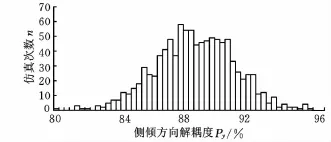
图5 优化前侧倾方向模态能量分布概率

图6 优化后垂直方向模态能量分布概率

图7 优化后侧倾方向模态能量分布概率

对比图4、图6可以得到，优化前垂直方向解耦度分布在32%～94%之间，差值为62%，优化后基本分布在81%～98%之间；对比图5、图7可以得到，优化前侧倾方向解耦度集中在81%～93%之间，优化后主要集中在89%～94%之间，标准方差为0.715。由此可见，优化后的解耦度分布较优化前更合理，优化结果具有较高的稳健性。

5 结语

本文将电动轮自卸车动力总成视为六自由度刚体，从能量解耦角度，运用优化拉丁方法分析了对总成悬置系统解耦布置影响较大的悬置静刚度参数，结合遗传算法与模拟退火法对各悬置刚度进行了优化设计，优化后系统固有频率配置更合理，各方向能量解耦度均得到提高；通过 Monte Carlo法进行分析可知优化结果基本满足稳健性要求。

［1］王峰，靳永军，张建武.基于整车模型的动力总成悬置振动仿真及优化［J］.振动与冲击，2008，27（4）：134-138.Wang Feng，Jin Yongjun，Zhang Jianwu.Vibration Simulation and Optimization of a Powertrain Mounting System Based on a Full Vehicle Model［J］.Journal of Vibration and Shock，2008，27（4）：134-138.

［2］Yu Yunhe，Naganathan N G，Dukkipatit R V.Review of Automotive Vehicle Engine Mounting Systems［J］.International Journal of Vehicle Design，2000，24（4）：299-319.

［3］周冠男，蒋伟康，吴海军.基于传递力最小的发动机悬置 系 统 优 化 设 计 ［J］.振 动 与 冲 击，2008，27（8）：56-57.Zhou Guannan，Jiang Weikang，Wu Haijun.Optimization Design of Engine Mount System by Minimizing the Total Force Transmission［J］.Journal of Vibration and Shock，2008，27（8）：55-57.

［4］Tao J S，Liu G R，Lam K Y.Design Optimization of Marine Engine Mount System［J］.Journal of Sound and Vibration，2000，235（3）：478-485.

［5］万海如，唐新蓬，段家典.重型矿用电动轮自卸车的现状和发展趋势［J］.汽车工业研究，2001（4）：16-22.Wan Hairu，Tang Xinpeng，Duan Jiadian.Present Status and Developing Trend of Heavy Duty Electric Wheel Dump Truck Used in Mine［J］.Auto Industry Research，2001（4）：16-22.

［6］Zavala P G，Pinto M G，Pavanello R，et al.Experimental and Computational Simulation Approaches for Engine Mounting Development and Certification［J］.SAE Technical Paper Series，2000-01-3239，2000.

［7］李令兵.发动机悬置系统设计流程及其分析与优化［D］.合肥：合肥工业大学，2007.

［8］Devi L，Ptasinski K J，Janssen FJJG.Pretreated Olivine as Tar Removal Catalyst for Biomass Gasifiers：Investigation Using Naphthalene as Model Biomass Tar［J］.Fuel Processing Technology，2005，86（6）：707-730.

［9］于德介，程军圣，杨宇.机械振动学［M］.长沙：湖南大学出版社，2010.

［10］付江华，史文库，沈志宏，等.基于遗传算法的汽车动力总成悬置系统优化研究［J］.振动与冲击，2010，29（10）：187-190.Fu Jianghu，Shi Wenku，Shen Zhihong，et al.Optimization for an Automotive Powertrain Mounting System Based on Genetic Algorithm［J］.Journal of Vibration and Shock，2010，29（10）：187-190.

［11］Bretl J.Optimization of Engine Mounting Systems to Minimize Vehicle Vibration［J］.SAE Paper，931322.

［12］龚旭，谷正气，李振磊，等.基于近似模型的集装箱半挂车导流罩的形状优化［J］.汽车工程，2011，33（1）：38-42.Gong Xu，Gu Zhengqi，Li Zhenlei，et al.Shape Optimization of Wind Deflector in Container Semitrailer Based on Approximate Model［J］.Automotive Engineering，2011，33（1）：38-42.

［13］金慧敏，马良.遗传退火算法在背包问题中的应用［J］.上海理工大学学报，2004，26（6）：561-564.Jin Huimin，Ma Liang.Genetic Annealing Evolutionary Algorithm Applied to the Knapsack Problem［J］.Journal of University of Shanghai for Science and Technology，2004，26（6）：561-564.

［14］张雨佳，遗传退火算法在城市配电网重构中的应用［D］.天津：天津大学，2007.

［15］石培成，陈无畏，高立新.基于蒙特卡罗法的动力总成悬置系统稳健性设计［J］.汽车工程，2010，32（8）：707-711.Shi Peicheng，Chen Wuwei，Gao Lixin.Robustness Design of Powertrain Mount System Based on Mote Carlo Method［J］.Automotive Engineering，2010，32（8）：707-711.