近场超声悬浮承载能力及影响因素的理论及实验研究

马希直 王胜光 王 挺

南京航空航天大学，南京，210016

0 引言

现代高科技研究领域要求高精密的运动及支承定位元件，如微细和纳米器件的加工设备、超净环境下集成电路硅片的无接触输运装置等，特别是那些要求低摩擦、低磨损、无油润滑领域中的设备。传统支承方式已无法满足要求，需开发高精度的新概念支承部件［1-4］。

气体轴承具有摩擦因数小、功耗低、精度高、无污染等优点，是一种理想支承部件，被广泛用于精密仪器、机床及高速旋转机械中，也被用于高温、低温以及具有辐射的环境中。动压及静压支承需要表面相对运动或者外部压力气体，使其在一些特殊场合的应用受到了限制。超声气体挤压膜支承兼有动压润滑和静压润滑的优点，有着广阔的应用前景，特别是可应用在动压和静压支承不能满足要求的场合，因而对气体挤压膜的特性进行分析具有重要的意义。

国内外对气体挤压膜性能已进行了较深入的研究并取得了一定的成果。美国IBM公司以及Michagan州立大学进行了挤压膜性能的早期研究［5］；以色列的 Minikes等［6-7］对挤压圆盘进行了机电耦合分析；英国的Stolarski等［8］以及日本的Yoshimoto等［9］对气体挤压膜轴承的结构进行了创新，发明了多种新的气体挤压膜轴承结构；在国内，常颖等［10］、彭太江等［11］基于超声理论对气体挤压膜轴承性能进行了初步研究。目前，对超声挤压膜悬浮性能及其支承的研究仍很不够，需要在气体挤压膜理论及应用方面进行更为深入的研究，特别需要研究高频挤压时的惯性、非连续、变形以及热等因素的影响，发明新的高性能挤压膜轴承及其控制系统。此外，随着微机电技术的进步，机械结构特征尺寸越来越小，润滑间隙已接近与表面粗糙度相当的量级，因此表面粗糙度对气体挤压膜承载能力的影响已不可忽视［12-15］，也需要进行深入研究。

本文主要针对固定以及自由悬浮圆盘模型建立气体挤压膜性能及其影响参数的计算模型，应用非线性数值解法对模型进行求解，研究了超声气体挤压膜的性能特点，分析了表面粗糙度对气体挤压膜承载能力的影响，另外还对挤压膜的性能进行了初步的实验测试。

1 理论模型建立

1.1 考虑表面粗糙度的挤压膜压力方程

挤压膜的原理如图1所示，下部是高频振动的激励圆盘，上部是固定圆盘或者自由悬浮圆盘，两圆盘之间是厚度为hT的挤压气膜。

图1 气体挤压膜原理示意图

一般假设挤压过程中两盘始终平行，气膜分布具有轴对称特点，则柱坐标下对应的可压缩气膜Reynolds方程为

式中，r为径向坐标，m；t为时间，s；p 为气膜压力，Pa；hT为气膜厚度，m；，η 为气体黏度，Pa·s；ρ 为气体密度，kg／m3。

对于随机二维粗糙表面模型，本文选用较为简单的Christensen模型进行初步分析，对式（1）进行修正，量纲一化后得

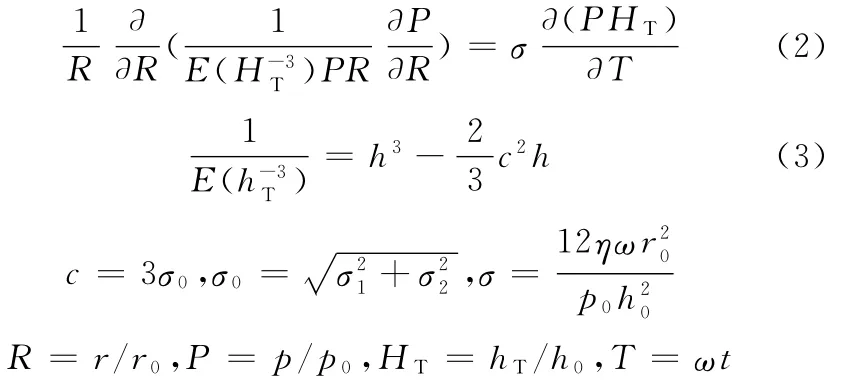
式中，σ1、σ2分别为两个挤压表面的粗糙度标准差，m；σ为挤压数；p0为环境压力，Pa；h0为初始气膜厚度，m；E（·）为数学期望；ω为激励圆盘运动的角频率；c为表面粗糙度系数，m；，r0为圆盘半径，m；h为不考虑粗糙度的气膜厚度，m。

1.2 初值及边界条件

1.3 考虑表面粗糙度的气膜厚度公式

在超声悬浮模型中，两盘之间的膜厚如下。对于固定悬浮体，瞬态膜厚由激励盘位移以及表面粗糙度两部分组成：

式中，ε为振幅比，ε＝a／h0；a 为激励盘振幅，m；Δ（R，θ）为量纲一表面粗糙度，Δ（R，θ）＝δ／h0；δ为表面粗糙纹理高度，m；θ为圆盘的周向坐标，rad。（轴对称边界条件）；量纲一初始条件为

对于自由悬浮体模型，气膜厚度由激励盘位移、悬浮体的悬浮高度y（T）、表面粗糙度影响三部分组成：

1.4 气膜承载力公式

对气膜压力进行面积分即可获得挤压膜的承载能力。瞬态量纲一承载力为

挤压膜的实际承载效应是气膜承载力的时间平均效应，一个振荡周期内的气膜平均承载力为

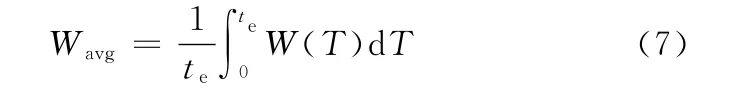
式中，te为激励圆盘的运动周期，s。

1.5 悬浮圆盘的运动方程

工程实际中，自由悬浮体比固定悬浮体情况更为常见，通常的支承器件都可以简化为自由悬浮体，根据动力学原理建立悬浮盘运动方程可获得自由悬浮盘的运动规律。自由悬浮状态下的悬浮盘运动方程为

式 中，m 为 悬 浮 盘 质 量，kg；g 为 重 力 加 速 度 （取9.8m／s2）。

2 计算结果及讨论

2.1 固定盘气膜瞬态过程分析

对挤压膜性能及悬浮体悬浮状态进行分析需要求解Reynolds方程，以获得挤压膜的气膜压力。式（2）为二阶非线性抛物型方程，综合考虑收敛精度、稳定性及计算量等因素，本文采用非线性盒式差分格式［16］以及迭代方法进行求解。

对于固定悬浮体模型，可以直接求解式（2）得到气体挤压膜的相关性质，而对于自由悬浮体的运动情况，需要联立求解Reynolds方程及运动方程，获得悬浮盘的悬浮高度y，运动方程为非线性二阶微分方程，采用Runge-kutta法进行求解。

本文首先对固定悬浮问题进行求解，求解模型相关参数如表1所示。

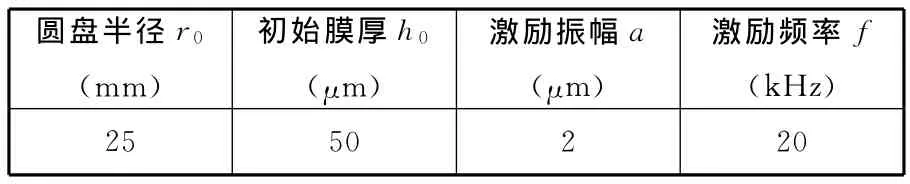
表1 固定圆盘计算参数

对固定圆盘压力方程进行求解，可以得到固定圆盘的瞬态压力分布。对应表1的计算参数，气膜压力分布如图2所示。由图2可知，圆盘沿半径方向上各点的压力在高频挤压过程中变化较小，在出口处压力有所升高，而沿时间方向，压力变化剧烈且会出现负压。

图2 固定圆盘气膜压力分布

保持圆盘半径以及初始膜厚固定不变，改变激励频率及振幅，得到不同激励频率和振幅下气膜的平均承载力，计算结果如图3所示。对于某一给定的激励振幅，气膜的平均承载力随着激励频率的增大而增大。而在同一激励频率下，气膜承载力随着激励振幅的增大明显的增大。

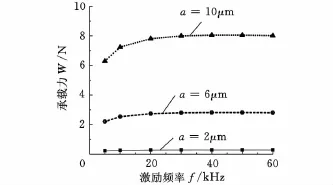
图3 气膜平均承载力与频率的关系（h0＝50μm）

为考虑表面粗糙度的影响，给定初始膜厚h0为50μm，激励振幅a 为2μm，激励频率f 为20kHz，计算得到不同表面粗糙度系数下的气膜承载力曲线，见图4。可以看出，表面粗糙度对气体挤压膜的承载能力有较大影响。随着粗糙度幅值的增大，承载力也逐渐增大，但过大的表面粗糙度会导致振动过程中粗糙峰穿透气膜而与圆盘表面接触，经分析，为提高承载能力，应尽量使表面呈圆环形纹理。

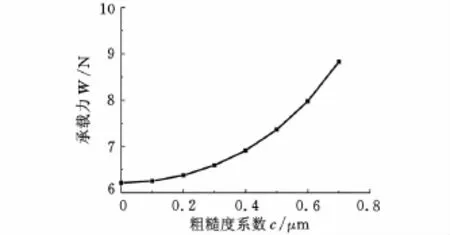
图4 粗糙度对气膜平均承载力的影响（h0＝50μm，a＝2μm，f＝20kHz）

2.2 自由悬浮体的瞬态响应过程

对于自由悬浮圆盘模型，其气膜瞬态压力分布如图5所示，表示在整个挤压过程中，从开始挤压到稳定的不同时间节点上沿半径方向的压力分布情况。在半径方向以及时间轴方向，除圆盘边缘外的各点上的压力都在变化，并且有时高于环境压力，有时低于环境压力。

图5 悬浮盘瞬态气膜压力分布

图6所示为圆盘由起浮到达稳定状态的过程中承载力变化曲线，图中每条曲线对应一个不同的初始膜厚h0。由图6可知，气膜承载力有一个从波动到稳定的瞬态过程，气膜承载力从起浮到稳定约需要60～90ms。图7所示为承载力达到稳定后一个周期内的气膜承载力的变化情况，由图可见，虽然初始膜厚不同，但稳态后气膜承载力却很接近。稳态气膜承载力有正有负，但在一个周期内的平均值大于零，因此气体挤压膜承载力的产生需要一定的时间。

表2给出了计算条件，计算结果如图8所示。图8中曲线是不同初始膜厚的圆盘悬浮高度响应曲线，可见，不管初始膜厚多大，最后稳定悬浮高度都约为31μm。自由悬浮盘从初始位置经历一个过渡过程后最终停留在一个确定高度做小幅振动，振幅约为膜厚的1／1000量级。稳定悬浮高度与初始膜厚无关，其大小取决于激励振幅、激振频率、圆盘半径以及悬浮盘质量等因素。

图6 悬浮盘气膜瞬态承载力曲线

图7 气膜承载力的周期性变化

表2 悬浮圆盘计算参数（圆盘质量m＝0.2kg）

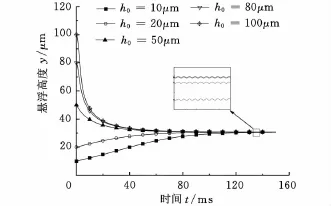
图8 不同初始高度时悬浮盘位移响应曲线（a＝2μm，f＝20kHz）

为了研究悬浮高度的影响因素，对不同频率和不同激励振幅下的悬浮高度进行了求解。计算结果如图9所示。由图9可知，悬浮盘最终悬浮高度随激励频率的增大而增大，但最终趋于一个极限值；随着激励振幅的增大悬浮高度明显增大，这一结论与固定悬浮体得到的结果一致。

同样，当其他条件不变时，可以得到不同激励振幅下表面粗糙度对悬浮高度的影响关系，结果如图10所示，可见增大表面粗糙度可以增加悬浮盘的悬浮高度，并且对于不同的激励振幅，其效果不同，由图10可以看出，随着振幅增大，粗糙度的影响逐渐减小。

图9 悬浮高度与频率的关系（h0＝100μm）

图10 悬浮高度与表面粗糙度的关系

3 实验原理及结果对比

为深入理解超声挤压膜的性能特点并验证模型的准确性，本文对超声悬浮承载能力以及悬浮高度进行了实验测试，实验台原理如图11所示，系统组成如图12所示。信号源产生的激励信号经过功率放大器放大后驱动压电换能器，换能器通过变幅杆驱动激励圆盘高频振动，在激励圆盘的上部是固定圆盘或悬浮圆盘，可以通过一个弹性力传感器以及激光位移传感器测量激励的振幅、承载能力及悬浮高度等，图13为实验系统的实物图片。

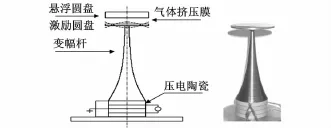
图11 实验装置示意图

图12 实验系统组成

实验所用圆盘的表面经车削加工并抛光制成，其表面纹理是同心圆形式（图14a），表面粗糙度纹理经光学放大镜及表面形貌仪测量，结果如图14b所示，经测量，表面粗糙度Rz≈0.4μm。

图13 实验系统图片

图14 实验圆盘的表面形貌

实验主要完成了以下两方面的内容：激励圆盘的振幅测量，固定圆盘的承载能力测试以及悬浮圆盘的悬浮高度测量。实验条件如下：激励信号取正弦信号，根据实验台特性取激励频率f＝20.5kHz，激励电压U分别取100V，200V，300V；实验中采用的位移传感器LK-G5000的精度为0.01μm，最高测量频率为392kHz，力传感器为应变型力传感器，其测量精度达0.01N，满足实验要求。

经测量，实验台中的激励圆盘在给定的三种电压条 件 下，盘 的 振 幅 分 别 为 1.1μm，2.5μm 和3.6μm。固定圆盘承载能力测量结果见表3。

表3 气膜承载力测量结果

自由悬浮盘的结构尺寸及质量见表4。经反复测量，所得自由悬浮圆盘的悬浮高度见表5。

表4 实验中用到的悬浮盘参数

表5 悬浮盘悬浮高度测量结果

4 结论

（1）气体挤压膜的承载能力主要由结构尺寸及激励特性决定。对于已经确定结构尺寸的挤压膜，气膜承载力的提高主要取决于激励盘的振幅及频率。增大激励盘的振幅对气体挤压膜压力的提高非常明显，采用压电堆或设计特殊结构对压电陶瓷的振幅进行放大是行之有效的方案。提高激励频率对气体挤压膜的承载能力也有较明显的影响，但这一影响是有限的，当频率达到到一定范围时气体挤压膜的承载能力趋于稳定。

（2）通过选取合适的加工工艺，在圆盘表面上得到了合理的纹向，可在一定程度上增大气膜的承载能力。

（3）设计了相应的实验设施，对挤压膜的承载能力、悬浮高度以及悬浮高度响应进行了测试，经与理论分析结果比较，二者较为一致。

上述结果可以作为超声悬浮器件设计的参考，为挤压膜理论进一步的研究打下一定基础。本研究尚有许多不足，如粗糙度模型较为简单、理论模型没有考虑惯性力影响等，需要进一步完善。

［1］Vandaele V，Lambert P，Delchambre A.Noncontact Handling in Micr-oassembly：Acoustical Levitation［J］.Precision Engineering，2005，29：491-505.

［2］Stolarski T A.Numerical Modeling and Experimental Verification of Compressible Squeeze Film Pressure［J］.Tribology International，2010，43：356-360.

［3］Izuno Yuji，Yoshimoto Shigeka，Miyatake Masaaki.Impulse-load Dynamics of Squeeze Film Gas Bearings for a Linear Motion Guide［J］.Journal of Tribology，2009，131：1-6.

［4］魏彬，马希直.考虑激振模态的挤压膜悬浮导轨特性分析［J］.润滑与密封，2010，35（2）：32-35.Wei Bin，Ma Xizhi.Research on the Characteristics of the Squeeze Film Floating Guide Way Including the Mode Effect［J］.Lubrication Engineering，2010，35（2）：32-35.

［5］Salbu E O J.Compressible Squeeze Films and Squeeze Bearings［J］.ASME J.of Basic Eng.，1964，86（3）：355-366.

［6］Minikes A，Bucher I.Levitation Force Induced by Pressure Radiation in Gas Squeeze Films［J］.J.Acoustic.Soc.Am.，2004，116（1）：217-226.

［7］Minikes A，Bucher I.Coupled Dynamics of a Squeeze-film Levitated Mass and a Vibrating Piezoelectric Disc：Numerical Analysis and Experimental Study［J］.Journal of Sound and Vibration，2003，263：241-268.

［8］Stolarski T A，Wei Chai.Self-levitating Sliding Air Contact［J］.International Journal of Mechanical Sciences，2006，48：601-20.

［9］Yoshimoto Shigeka，Kobayashi Hiroyuki，Miyatake Masaaki.Float Characteristics of a Squeeze-film Air Bearing for a Linear Motion Guide Using Ultrasonic Vibration［J］.J.of Tribology International，2007，40（3）：503-511.

［10］常颖，杨志刚，吴博达，等.超声波轴承悬浮性能及承载力的实验研究［J］.压电与声光，2004（4）：197-199.Chang Ying，Yang Zhigang，Wu Boda，et al.Experi Ment Study on the Performance of Suspend and Bearing the Load of Ultrasonic Bearing［J］.Piezoelectrics ＆ Acoustooptics，2004（4）：197-199.

［11］彭太江，杨志刚，阚君武，等.超声波悬浮能力及其试验研究［J］.压电与声光，2006，28（4）：229-235.Peng Taijiang，Yang Zhigang，Kan Junwu，et al.Experiment Research on Ultrasonic Levitation Ability［J］.Piezoelectrics ＆ Acoustooptics，2006，28（4）：229-235.

［12］Christensen H.Stochastic Model for Hydrodynamic Lubrication of Rough Surfaces［J］.Proc.Inst.Mech.Eng.，1969，184：1013-1026.

［13］White J W.The Effect of Two-Dimensional Surface Roughness on the Load-Carrying Capacity of a Thin Compressible Gas Film［J］.Journal of Tribology，1993，115（2）：246-252.

［14］Mitsuya Y，Ohkubo T，Ota H.Averaged Reynolds Equation Extended to Gas Lubrication Possessing Surface Roughness in the Slip Flow Regime：Approximate Method and Confirmation Experiments［J］.Journal of Tribology，1989，111（7）：495-503.

［15］Tonder K.A Numerical Assessment of the Effect of Striated Roughness on Gas Lubrication［J］.Journal of Tribology，1984，106（7）：315-321.

［16］陆金甫，关治.偏微分方程数值解法［M］.北京：清华大学出版社，2004.