新型锯丝的弹塑性冷绕成形与回弹研究

姚春燕 陈思源 彭 伟

浙江工业大学特种装备制造与先进加工技术教育部重点实验室，杭州，310032

0 引言

太阳能光伏发电产业的迅猛发展对硅片的切割加工技术提出了更高的要求。目前，硅片切割主要采用多线锯切割的方式，即在研磨液配合下，用高强度超细切割钢丝将单晶硅或多晶硅的基体硅锭锯切成片。切割用线锯主要包括游离磨料线锯和固结磨料线锯两大类。在工业应用领域，基体硅片的切割通常采用游离磨料线锯，但这种切割方式存在着生产效率低下、环境污染严重及研磨液后续处理成本较高等主要缺点。由此，彭伟等［1］提出了一种全新的线锯切割技术。这种新型线锯的主要特点是：在超细琴钢丝的基体（内线）表面，包覆有较耐磨与耐拉的金属丝线（外线，如碳素弹簧钢丝等）冷绕成形的致密微细槽型。为保证锯丝缠绕的强度与稳定性，冷绕外线的直径应小于基体内线的直径，且满足跨高比，从而忽略剪切变形在冷绕过程中对横截面的影响。

锯丝冷绕成形时，外线将承受较大的弹塑性弯曲，而弹性部分卸载后的恢复使得成形后曲率有所减小，因此，外线冷绕弯曲存在回弹的问题［2］。影响回弹的因素很多，很难从理论上精确计算弯曲的回弹量并通过现有的工艺来完全避免回弹。回弹的存在使弯曲后的制件尺寸精度降低并产生形状误差，它是制约弯曲件生产质量、成本，并限制生产效率的关键因素之一，也是弯曲成形中亟待解决的质量问题［3-6］。

最早的简单弯曲回弹研究始于20世纪50年代，Gardiner等基于弯曲理论模型对理想弹塑性板弯曲及回弹问题进行了研究［7］。而采用数值模拟方法对实际存在的复杂弯曲回弹问题研究始于20世纪70年代［8-9］。尽管各国学者在板料弯曲回弹方面做了大量工作，但对于钢丝的弯曲成形及回弹问题研究则较少。已有钢丝、钢管等的弯曲回弹研究大多采用类似于板材的弯曲回弹理论［10-11］。孔灿［12］针对口腔正畸不锈钢丝，运用有限元方法对其弯曲成形和回弹问题进行了模拟；Tang［13］根据塑性理论对管材弯曲中的应力分布、壁厚变形及弯矩等进行了分析；张立玲［14］根据弯曲条件下的应力应变分析和回弹理论，推导了管材回弹量的计算公式；刘志刚等［15］依据恒力场理论和弹性极限回弹理论，采用分段曲线型和折线型法，通过试弯确定了回弹角公式。这些文献大都从弹塑性纯弯曲理论出发，讨论钢丝、钢管等弯曲时截面内的应力与应变、弯矩与曲率以及回弹的问题。但是，新型锯丝的冷绕成形是一个蕴含了拉伸和弯曲的复合变形过程，是一种包含几何非线性、材料非线性和边界非线性在内的复杂非线性问题。

为了清晰地揭示新型锯丝在冷绕成形过程中的弯曲变化规律及回弹对锯丝内外线径所带来的影响以提高锯丝成形的精度，本文基于理想弹塑性材料本构关系的弯曲及弹性卸载理论，以解析的方法对锯丝冷绕成形及回弹问题进行了分析，以期为后续的研究提供参考。

1 锯丝冷绕成形过程分析

锯丝（图1）的冷绕成形是一个外线沿着弯曲线逐渐变形的过程，也是一个锯丝横截面由外至内逐渐变形的过程，因此，外线的弯曲过程经历了弹性应力应变和塑性应力应变的不同变形阶段，这种连续渐进的变形路径会对弯曲卸载后的回弹产生复杂的影响。

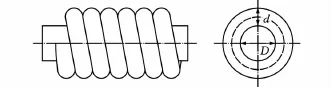
图1 锯丝的结构示意图

弯曲初期，弯矩较小，外线处于较大曲率状态，只产生弹性变形。随着弯矩的增大，当曲率达到一定值时，外线开始产生塑性变形。当弯矩继续增大，塑性变形由外部向内部扩展，塑性变形区域不断扩大，而弹性变形区域则因曲率的增大而不断减小。

在实际冷绕过程中，外线由摩擦力产生轴向张紧而时刻处于拉直状态，故除弯矩作用下的纯弯曲，若考虑外线拉直状态下所受的轴向力影响，其力学模型即为拉伸弯曲组合模型，如图2所示。

图2 拉伸弯曲组合变形下的力学模型

2 外线弹塑性弯曲及其应力分析

2.1 外线弯曲变形的基本假设

为简化数学上的运算且在不影响外线弯曲的回弹分析基础上，采用如下基本假设：①外线材料是各向同性且均匀的，不考虑各向异性的影响；②单向应力假设，外线在弯曲过程中的轴向纤维之间没有挤压错位，横截面上仅承受沿轴线方向的拉应力或压应力；③平截面假设，外线弯曲前的横截面变形后仍保持为平面，且和变形后的轴线正交；④外线采用理想弹塑性材料的应力应变模型，且在使用范围内拉伸与压缩曲线相同，如图3所示；⑤不考虑外线在冷绕成形过程中产生的横截面扁化、外壁拉裂和内壁起皱影响；⑥成形外线卸载时遵循弹性卸载规律，且不会发生反向屈服。

图3 理想弹塑性材料应力－应变曲线

2.2 外线弯曲成形的弹塑性分析

记外线半径为ro，内线半径为ri，当外线在弯矩与轴向力的共同作用下时，任意截面上的载荷均保持不变并只引起截面的轴向应力。其中弯矩是造成外线弯曲变形的最主要因素，它使变形区的外侧材料受到拉伸，在中性层上方截面产生轴向拉应力，内侧材料受到压缩，在中性层下方截面产生轴向压应力。而轴向力始终垂直于弯曲后的横截面，并且只产生轴向拉应力作用，其结果使外线的上半截面拉应力总是大于下半截面拉应力，上侧外缘较下侧外缘也更快达到屈服，同时中性轴也将向下发生偏移。

起初弯矩和轴向力较小，整个截面不存在塑性屈服，截面弹性应力呈三角形直线分布，可称为完全弹性应力阶段，如图4a所示。随着弯矩的逐渐增大，轴向力大小保持不变，由于上半截面的拉应力比下半截面拉应力大，故上半截面外层纤维应力将首先达到屈服应力并开始进入塑性阶段，而下半截面仍处在弹性阶段。上半截面应力呈梯形折线分布，下半截面应力呈三角形直线分布，并仅在上半截面外层出现塑性屈服区，可称为单边弹塑性应力阶段，如图4b所示。当弯矩继续增大，下半截面外层纤维应力达到屈服应力并进入塑性阶段时，上半截面的塑性区域不断向内层延伸扩大，从而使截面内外层都出现塑性屈服区，中性轴开始向截面形心轴靠近，截面应力呈梯形折线分布，可称为双边弹塑性应力阶段，如图4c所示。图4中，中性轴偏移截面形心轴的距离设为b，弹塑性交界面到中性轴的距离为μro（0≤μ≤1）。

2.3 双边弹塑性阶段弯矩M 与弯曲半径ρ的关系

图4 弯曲成形三个阶段的应力分布

对于钢材设计，一般不完全利用塑性的极限弯矩强度，而只考虑截面内部分发展塑性［16］，故外线在最后的弯曲成形阶段截面应力多为双边弹塑性应力分布。由图4c、图4d可知，其截面正应力σ应为

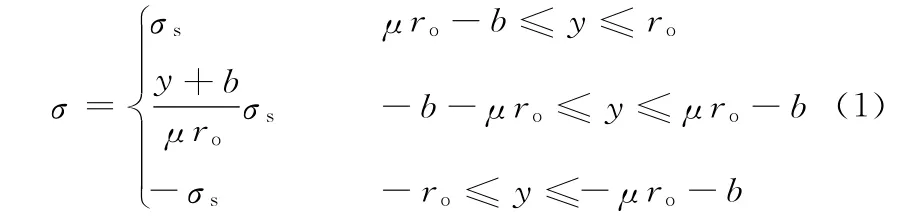
式中，σs为外线材料的屈服应力；y为截面内任一点到截面形心轴的垂直距离。

外线所受弯矩与截面正应力的关系为

由图4d可知，在外线截面上任取一平行z轴的微元矩形，由几何关系可计算该微元面积为

在双边弹塑性阶段，外线截面上所承受的弯矩由上侧塑性区弯矩、中部弹性区弯矩和下侧塑性区弯矩共同组成，将式（1）、式（3）代入式（2），分别计算三部分弯矩如下。

（1）上侧塑性区弯矩为

对式（4）积分并整理可得

（2）中部弹性区弯矩为

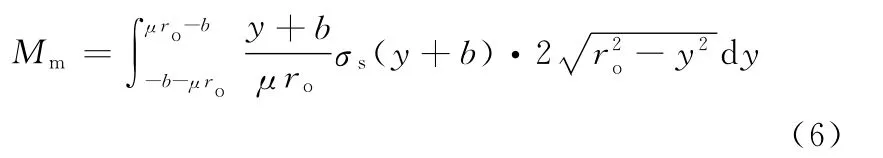
对式（6）积分并整理可得

（3）下侧塑性区弯矩为

对式（8）积分并整理可得

故整个截面的弯矩为

将式（5）、式（7）、式（9）代入式（10）并整理可得

式中，E为外线材料的弹性模量；F为外线受到的轴向力；ρ为中性层的弯曲半径。

不同于完全弹性阶段弯矩M与曲率（1／ρ）之间的简单线性关系，式（11）表明：弹塑性成形阶段，在轴向力的影响下外线弯矩与曲率之间存在着复杂的非线性关系。

3 外线卸载回弹分析计算与控制

3.1 卸载回弹分析

外线冷绕完成后，将以加载弯矩M和轴向力F进行卸载，这可看作是对外线施加一个反向加载弯矩M和反向轴向力F所产生的弹性弯曲效应，但轴向力的弹性弯曲效应不会影响弯曲回弹，仅有弯矩和回弹半径服从弹性关系。

对于塑性成形阶段，弯矩与弯曲半径之间为非线性关系，故直接计算卸载弯矩存在一定困难。因外线所受轴向力仅由外线轮的摩擦力提供，其值很小几乎不造成变形，故在不影响回弹分析的基础上，令轴向力F＝0，此时外线冷绕的拉弯过程即为纯弯过程，式（11）变为

式中，Me为外线材料的弹性极限弯矩；ρe为外线材料的弹性极限弯曲半径。

显然对于纯弯过程，其塑性阶段的弯矩与曲率之间仍为非线性关系。为便于进一步讨论，不妨令

卸载阶段相对弯矩与曲率之间的关系与弹性阶段相同：

图5 弯矩－曲率曲线图

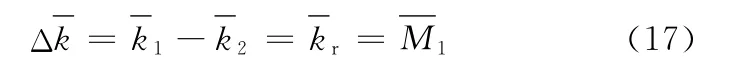
将式（18）代入式（17），再按式（14）进行换算后得

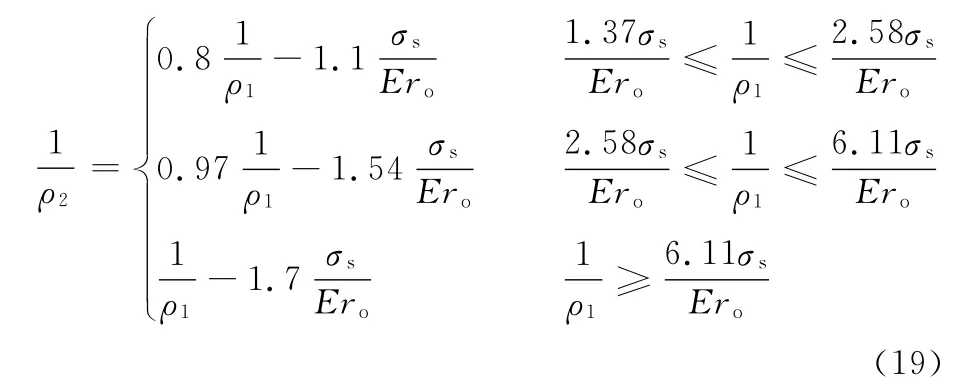
式中，ρ1为成形弯曲半径；ρ2为残余弯曲半径。

3.2 锯丝冷绕内外线径理论计算公式

锯丝冷绕成形时，内外线的几何关系如图2所示，将ρ1＝ro＋ri与ρ2＝r代入式（19）并化简可得到内外线径的理论计算公式如下：

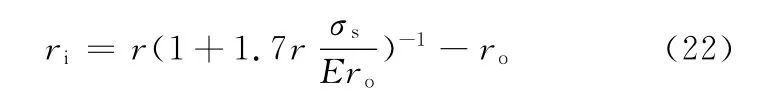
式中，r为名义半径，为锯丝冷绕成形后的实际半径与外线半径之差。

3.3 锯丝冷绕线径计算及实验研究

以冷绕新型锯丝为例，内外线采用理想弹塑性体的超细弹簧钢丝。 已知：内线直径为0.16mm，抗拉强度σb为2200MPa，外线直径为0.08mm，抗拉强度σb为2400MPa，屈服强度σs＝0.9σb，弹性模量E＝2.06×105MPa，计算冷绕成形后锯丝的名义直径如下。

内外线径跨高比为 π（0.16＋0.08）／0.08＝9.42＞7，若整个冷绕过程中锯丝无卸载回弹影响，则理论上成形后的实际直径（图1）应为

式中，dr为实际绕后直径；di为内线直径；do为外线直径。

现考虑卸载回弹带来的影响，将示例中的数据分别代入式（20）～式（22）中，各公式下计算的名义直径及适用范围列于表1中。

表1 计算结果 mm

由表1知，本例应选用式（22）所计算的结果作为冷绕成形后锯丝的名义直径（0.254mm），则实际直径应为

相比理论计算直径的0.32mm，由于回弹的存在，成形后的实际直径增大了近5.8%。

为验证公式计算结果的可靠性，采用自行研制的JG-52C新型线锯缠绕设备进行锯丝的冷绕成形实验，并应用VW-6000／5000三维显微系统进行尺寸的观察与测量，实验设备及观测平台如图6所示。

图6 冷绕实验设备及观测平台

为尽量减少由于实验所用内外线本身的椭圆度及直径误差对观测造成的影响，首先采用预绕张紧的方式来测量外线紧绕在内线表面（无回弹）时的截面直径尺寸，放大倍率设置为300倍，如图7所示。

图8为经缠绕设备冷绕成形并已卸载回弹后锯丝的实测直径尺寸，放大倍率设置为300倍。

卸载回弹后锯丝的实测直径为333.89μm，而由公式计算所得直径为334μm，误差为0.03%。说明采用公式计算回弹后的锯丝直径具有较高的可靠性，满足工程上对精度的要求。可见，回弹的存在将直接影响锯丝最后的成形精度。

图7 实验内外线尺寸观测（×300）

图8 卸载回弹后的锯丝实测直径尺寸（×300）

3.4 锯丝冷绕成形回弹控制

通过上述分析，为保证锯丝最后的成形精度，应当采取必要可行的措施来减小和控制回弹带来的影响［18］：①在满足成形锯丝使用要求的条件下，外线尽量选取弹性模量大、屈服极限小的材料；②采用拉弯工艺［19］，加大轴向力使中性层内外均处于拉应力状态，使得卸载后的部分回弹相互抵消；③锯丝冷绕前可在内线表面预先涂覆黏结剂，外线冷绕成形后再进行相关的固化，从而将外线粘附在内线表面；④对成形后的锯丝进行热处理，以减小外线内部的弯曲应力等。

由于卸载回弹是锯丝成形的最后一步，而成形过程中产生的任何误差都会累积到回弹计算阶段，因此有必要对其进行更为深入的研究和有效的控制。

4 结论

（1）基于理想弹塑性材料本构关系的弯曲理论，建立外线在拉弯组合下的力学模型进行弯曲成形的弹塑性分析，按截面应力分布将其成形过程划分为完全弹性应力、单边弹塑性应力及双边弹塑性应力三个阶段。针对双边弹塑性应力阶段建立了轴向力影响下弯矩与弯曲半径之间的数学关系式。

（3）从材料和工艺两个方面，提出了减小和控制锯丝成形后回弹的四项措施，对新型锯丝的生产具有一定的实际应用价值。

［1］彭伟，王金生，姚春燕.亚固结线锯切割实验研究［J］.中国机械工程，2013，24（9）：1125-1128.Peng Wei，Wang Jinsheng，Yao Chunyan.Experimental Study of Semi-fixed Wire Sawing［J］.China Mechanical Engineering，2013，24（9）：1125-1128.

［2］臧顺来，郭成.基于非线性弹性卸载的L形弯曲成形回弹研究［J］.中国机械工程，2006，17（增刊1）：44-47.Zang Shunlai，Guo Cheng.An Investigation on Spring-back of L-bending Sheet Metal Forming Based on Non-linear Elastic Unloading［J］.China Mechanical Engineering，2006，17（S1）：44-47.

［3］陈英杰.梁和薄板的回弹变分原理研究与应用［D］.秦皇岛：燕山大学，2005.

［4］蔡中义，李明哲，李湘吉.板材成形回弹数值分析的静力隐式方法［J］.中国机械工程，2002，13（17）：1458-1461.Cai Zhongyi，Li Mingzhe，Li Xiangji.Static Implicit Approach of Springback Simulation for Sheet Metal Forming［J］.China Mechanical Engineering，2002，13（17）：1458-1461.

［5］雷松，王时龙，冯治恒，等.螺旋弹簧冷绕成形与回弹的数值分析［J］.计算机工程与应用，2011，47（27）：228-232.Lei Song，Wang Shilong，Feng Zhiheng，et al.Numerical Analysis of Cold Coiling and Springback for Helical Springs［J］.Computer Engineering and Applications，2011，47（27）：228-232.

［6］刘婧瑶，唐承统，宁汝新.薄壁管纯弯曲塑性成型分析及回弹计算［J］.塑性工程学报，2009，16（2）：5-14.Liu Jingyao，Tang Chengtong，Ning Ruxin.Plastic-formation Analysis and Springback Calculating of Thin-wall Tube Pure-bending［J］.Journal of Plasticity Engineering，2009，16（2）：5-14.

［7］李建，赵军，展培培，等.板料自由弯曲成形及回弹理论解析［J］.塑性工程学报，2009，16（4）：1-6.Li Jian，Zhao Jun，Zhan Peipei，et al.Theoretic Analysis of Forming and Springback for Sheet Metal Air Bending［J］.Journal of Plasticity Engineering，2009，16（4）：1-6.

［8］余同希，章亮炽.塑性弯曲理论及其应用［M］.北京：科学出版社，1992.

［9］Huang M，Gerdeen J C.Springback of Double Curved Developable Sheet Metal Surface-an Overview［J］.SAE Paper，940938，1994.

［10］Hyunok K，Ninad M，Taylan A.Prediction Ofbend Allowance and Springback in Air Bending［J］.Journal of Manufacturing Science and Engineering，2007，129：342-351.

［11］Bibel G D，Kicher T P.Reduction of Springback and Residual Stresses during Winding of a Helical Spring［J］.Journal of Engineering for Industry，1991，113（2）：214-217.

［12］孔灿.正畸不锈钢弓丝弯曲成型与回弹的有限元数值模拟研究［D］.南京：东南大学，2009.

［13］Tang N C.Plastici-deformation Analysis in Tube Bending［J］.International Journal of Pressure Vessels and Piping，2000，77：751-759.

［14］张立玲.管材塑性弯曲回弹量计算［J］.锻压技术，2002（3）：37-39.Zhang Liling.Calculation of Springback in Pipe Bending［J］.Forging ＆ Stamping Technology，2002（3）：37-39.

［15］刘志刚，李祖光，林尉.弯管回弹问题探讨研究［J］.电站系统工程，1999，15（3）：60-65.Liu Zhigang，Li Zuguang，Lin Wei.Discussion on Rebound of Bent Tube［J］.Power System Engineering，1999，15（3）：60-65.

［16］王国周，瞿履谦.钢结构：原理与设计［M］.北京：清华大学出版社，1993.

［17］陈明祥.弹塑性力学［M］.北京：科学出版社，2007.

［18］范志明.弯曲回弹的减少与消除［J］.现代机械，2003（5）：36-37.Fan Zhiming.Deceasing and Eliminating Spring Back in Sheet Metal Forming［J］.Modern Machinery，2003（5）：36-37.

［19］吴建军，张贺刚，王俊彪，等.等边角型材带侧压型材拉弯的力学与回弹分析［J］.中国机械工程，2006，17（5）：542-548.Wu Jianjun，Zhang Hegang，Wang Junbiao.Mechanics and Springback Analysis for the Stretchbending Process of Extruded Profile with Lateral Compression［J］.China Mechanical Engineering，2006，17（5）：542-548.