相依计数变量风险模型的大偏差

宇世航,王德辉,魏蕴波

(1.齐齐哈尔大学 理学院,黑龙江 齐齐哈尔 161006;2.吉林大学 数学学院,长春 130012)

0 引言与预备知识

考虑基于下述条件的一类风险模型：

Nk=α∘Nk-1+εk,k=1,2,…,

(1)

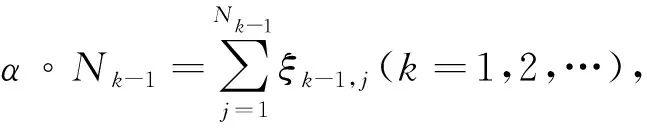
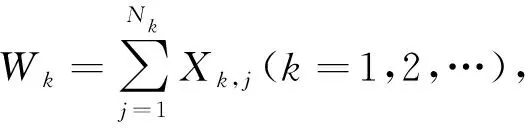
盈余动态过程模型为

(2)

其中:u表示保险公司初始资金;c表示单位收益率;Sk表示从第0到第k期累积索赔总额,即

Sk=W1+W2+…+Wk,

(3)

规定S0=0.

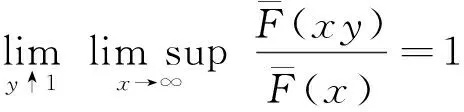
1 主要结果

证明: 注意FY∈C,对任意的θ>0和充分大的y,

因此,有

(4)

由引理1和式(4),存在某个δ>0,有

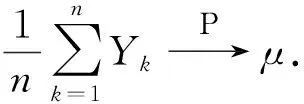
证明：对任意的ε>0,当n→∞时,有

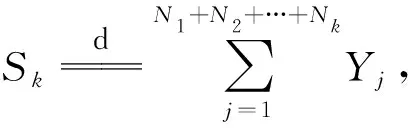
证明: 对任意实值r,Sk的特征函数为

另一方面,有

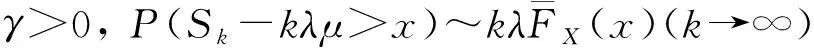
证明: 令{Y,Yj,j≥1}是与X同分布的i.i.d.序列,且与式(1)中定义的{Nk}独立.对任意的η>0,考虑

由引理1,对充分大的x,有

(6)

对x>γk一致成立.

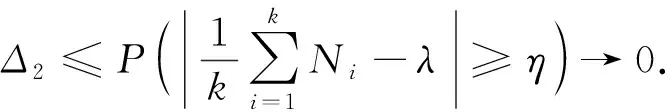
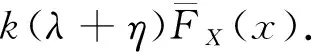
(7)

另一方面,

(9)

令η↓0,由式(7),(9)和定理1可证结论.

证明: 事实上,由定理1,只需证存在某个δ>0,使得

(10)

在x>γk1+δ上一致成立即可.类似定理2的证明,只需将引理2应用到式(5),(8)中即可证得式(10).

[1] Gerber H U.An Introduction to Mathmatical Risk Theory [M].Philadelphia: S S Huebner Foundation for Insurance Education,1979.

[2] Dickson D C M.Insurance Risk and Ruin [M].Cambridge: Cambridge University Press,2005.

[3] Hélène C,Etienne M,Véronique M D.Discrete-Time Risk Models Based on Time Series for Count Random Variables [J].Astin Bulletin,2010,1: 123-150.

[4] Hélène C,Etienne M,Florent T.Risk Models Based on Time Series for Count Random Variables [J].Insurance: Mathematics and Economics,2011,48(1): 19-28.

[5] Ng K W,TANG Qi-he,YAN Jia-an,et al.Precise Large Devitions for Sums of Random Variables with Consistently Varying Tails [J].J Appl Probab,2004,41: 93-107.

[6] SU Chun,TANG Qi-he.Characterizations on Heavy-Tailed Distributions by Means of Hazard Rate [J].Acta Math Appl Sinica: English Series,2003,19(1): 135-142.

[7] McKenzie E.Discrete Variate Time Series [J].Stochastic Processes: Modelling and Simulation,2003,21: 573-606.

[8] Al-Osh M A,Alzaid A A.First-Order Integer-Valued Artoregressive INAR(1) Process [J].Journal of Time Series Analysis,1987,8(3): 261-275.