Fermi架构下的SPSO算法加速

田 幂,胡 亮,车喜龙

(吉林大学 计算机科学与技术学院,长春 130012)

粒子群优化算法(PSO)具有稳健、 有效、 简易和适应性广的特点,应用广泛[1-4].标准粒子群优化算法(SPSO)[5]是对原始算法的直接扩展.尽管SPSO算法拥有许多优点,但在大规模问题,如在大维度和大群数上,仍需较长时间寻找解决方案.SPSO算法的结构存在内在的并行性,通过直接删除更新之间的依赖,编写同步PSO,同时允许粒子不严格依赖最新信息[6],放宽同步限制,可在并行计算架构下实现SPSO算法.

图形处理单元(GPU)因其并行计算机制和快速的浮点操作能力,在科学计算上展现出较强的优势,因此应用广泛.与其他加速平台相比,如CellBE和FPGAs,GPU已在HPC研究领域占主导地位[7],同时使用CUDA开发工具[8]可轻松地进行编程.

利用可编程的GPU加速SPSO算法的可行性与有效性已被证实[9-10],然而这些研究都没有利用最新的硬件版本[11].Fermi 同样是双架构设计,即CUDA计算架构和图形架构,两种架构可灵活切换,但Fermi几乎是重新设计并更注重通用计算架构.本文利用Fermi GPU的同时,在最新架构下实现了并行版本的SPSO算法.

1 SPSO算法与Fermi架构

1.1 SPSO算法

图1 SPSO算法流程Fig.1 Flowchart of SPSO

SPSO系统初始化是一群随机的粒子,并通过更新粒子寻找多维解决空间的最优值.每个粒子依据其自己发现的本地最近解决方案进行移动.相邻最佳解决方案由与其相邻的左邻居和右邻居发现.每次迭代中粒子更新其速度和位置直到满足终止条件.SPSO算法的基本流程如图1所示.

1.2 Fermi架构

程序可分为两部分：主机端部分和设备端部分.主机端部分在CPU上执行,管理数据的传输,上下文的预处理和后处理,调度设备端部分的执行； 设备端部分在GPU上执行,由一个或多个称为kernel的函数组成， 每个kernel是程序的一个并行单元,由许多并行的线程执行.Fermi架构支持不同kernel的同时执行,它的流水技术可减少应用上下文切换带来的开销,同时支持kernel间的快速通信.

线程是设备端部分程序的最小执行单位,以grid和block的形式组成.一个block由许多线程组成,同一block中的线程共享数据并同步它们的执行.同一kernel的一些block组成一个grid.线程以warp的形式进行调度和执行,同一warp内的所有线程可认为是同时运行的,存储访问也以warp形式工作.

Fermi GPU以图形处理集群可扩展阵列(GPC)为基础,每个GPC由4个流水多重处理器(SM)组成.每个SM有32个CUDA核,16个Load/Store(LD/ST)单元和4个特殊函数单元(SFU).CUDA核由全流水整数算术逻辑单元(ALU)和浮点单元(FPU)组成.一个GPU执行一个或多个grid； 一个SM执行一个或多个block； 一个ALU/FPU/SFU执行一个线程.

在GPU芯片外,有64位的GDDR5 DRAM,可视为是global memory，local memory，constant memory 和texture memory的组合,由主机端缓存和读写.Fermi对local memory，shared memory和global memory使用统一的地址空间完成加载和存储操作.在GPU芯片内,有3种类型的快速存储器：register files，shared memory和cache,它们由设备端进行读写操作.

2 SPSO算法在Fermi架构下的加速

SPSO算法在GPU上的执行过程如下.

算法1

1) 在global memory中申请所需的变量空间；

2) 将数据由主机内存拷贝到global memory内相应的变量中；

fori=1 to Iter do //并行执行for语句中步骤

3) 计算每个粒子的适应值；

4) 更新每个粒子的最佳适应值和最佳位置；

5) 更新粒子群的最佳适应值和最佳位置；

6) 更新每个粒子的速度和位置；

end for

7) 将结果数据由global memory拷贝回主机内存.

本文使用的主要参数如下：Iter表示SPSO算法的迭代次数；D表示每个粒子的维度；N表示粒子的数目.

2.1 加速策略

在Fermi上加速SPSO算法,需要考虑计算量与block维度的选择、 存储的使用和控制指令流的使用.

2.1.1 计算量与block维度的选择 如果计算规模很小,使用GPU进行计算将不能弥补传输数据带来的延时,即使用GPU计算的时间甚至比使用CPU计算的时间更长.所以要避免较小的计算规模,充分利用每个SM的计算能力.

单纯考虑计算规模还不够,block的大小最终影响SM上可运行的线程数量， 所以要选择合适的block维度,不仅要保证SM上可运行的线程数量,还要兼顾存储的使用情况.

2.1.2 存储的使用 对于global memory,如果可执行异步拷贝,在完成操作前,主机端就会获得返回值,从而CPU线程可继续执行余下操作， 所以可采用异步拷贝达到加速的目的， 同时应该合理布局global memory上的数据影响GPU的表现.

在每个SM中,register是有限的.当超过这个限制时,SM就会使用local memory存储.因为local memory的访问速度要慢于register的访问速度,所以应合理声明变量以减少local memory的使用.

在Fermi架构中,有一块64 Kb的RAM,可分成16 Kb的cache和48 Kb的shared memory,或48 Kb的cache和16 Kb的shared memory.前者有更大的shared memory,相应的cache较小,cache命中率就要降低;后者中,cache有足够的空间提高命中率.可针对不同的情况选择不同的划分方式以提高运行速度.

2.1.3 控制指令流的使用 控制流(if，switch，while和for)使线程跳到不同的分支.GPU在这种情况下,不同执行路径必须串行执行,且在所有的分支执行结束后,所有的线程才能回到相同的执行路径上.所以应减少分支数,可将一些控制流移到主机端执行,对于无法在主机端执行的控制流进行适当合并.

2.2 设计实现

本文给出算法1的主要实现过程.计算能力为2.x的GPU技术参数如下：每个SM上可运行的最大线程数为1 536； 每个SM上可运行的最大block数为8； 32位的register数量为32 K.

2.2.1 并行部分的实现 本文共实现4个经典的enchmark test函数,包括Sphere,Rastrigin,Griewangk和Rosenbrock.基于本文的加速策略,对算法1的步骤3),编写4个不同的kernel函数分别对应4个enchmark test函数,在主机端执行switch语句选择不同的kernel函数.对于算法1的步骤4)～6),4个enchmark test函数的操作是一致的,所以分别编写一个kernel函数.在kernel函数里,尤其是步骤5)中,不可避免使用if语句,要尽量合并这些if语句.

2.2.2 线程的分布和shared memory的选择 在算法1的并行部分中,用一个线程处理一个粒子,即一个线程代表一个粒子.在计算能力为2.x的GPU中,每个SM上可运行的最大线程数是1 536,SM的数量是15.所以为了最大限度地利用SM的计算能力,一次至少需要23 040个粒子.

在执行并行部分前,使用标志cudaFunc-CachePreferL1将RAM分成16 Kb cache 和 48 Kb shared memory,或 48 Kb cache和16 Kb shared memory,分别用存储1和存储2表示.在算法1的步骤6)中,需要使用最多的shared memory,设计使用5个大小为D×N的float类型数组,用于存储适应值和位置数据.为兼顾SM的计算能力和存储能力,并方便实验对比,将block的维度设计成3种：8×8,16×8 和 16×16,分别用维度1、 维度2和维度3表示.

2.2.3 Global memory和变量的使用 在算法1的步骤2)中,需要依次拷贝每个粒子的适应值、 最优适应值、 位置、 最优位置和速度及粒子群的最优适应值和最优位置,同时还有计算时所需的随机数， 使用cudaMemcpyAsync( )依次完成上述数据的异步拷贝.

设计数据在global memory中的存储方式,按维度依次存储每个粒子,即可认为是逻辑上的二维数组.在逻辑二维数组中,第j个粒子的第i维数据下标为(i,j),表示在大小为D×N的数组中下标为(i×N+j)的数据.这样的设计保证在同一个block中可同时计算每个粒子及其维度.

在CUDA中有一些内建的变量如threadid和blockid,在kernel函数中,避免不必要的变量声明并最大限度地使用内建变量.

2.2.4 粒子的限制 使用

(1)

计算关于shared memory的使用情况[6].在计算能力为2.x的GPU中,shared memory最大为48 Kb,结合式(1),可得:

(2)

不等式(2)的前半部分表示粒子位置、 速度和最优位置及粒子群的最优位置所占存储的大小,后半部分表示适应值、 粒子最优适应值和粒子群最优适应值所占存储的大小.一个float类型数据的大小是32位,根据式(2),D的取值是o(103).为实现“无限个”粒子,在设计中通过使用循环完成.

3 实验结果与分析

实验条件：Windows XP操作系统,Visual Studio 2005编程工具,cudaToolkit3.1.GTX480,Inter(R)Core(TM)2 Duo CPU E5700@2.93 GHz和Dell Optiplex360.

实验选取4个函数：Sphere,Rastrigin,Griewangk和Rosenbrock， 分别表示如下：

参数设定：N=105,D=50,Iter=5 000;时间1表示文献[10]的运行时间,时间2表示多核CPU运行时间,时间3表示本文优化后CPU的运行时间； 数值1表示CPU上的适应值,数值2表示多核CPU上的适应值， 数值3表示GPU上的适应值.

3.1 Block维度和shared memory的影响

在2.2.2中所述的3种block维度选择和2种RAM划分情况下,在f1～f4函数上运行SPSO算法,运行时间分别列于表1～表4.

表1 Sphere函数上的运行结果Table 1 Results of Sphere function

表2 Rastrigin函数上的运行结果Table 2 Results of Rastrigin function

表3 Griewangk函数上的运行结果Table 3 Results of Griewangk function

表4 Rosenbrock函数上的运行结果Table 4 Results of Rosenbrock function

实验结果表明,当block的维度为16×8,RAM划分成48 Kb的cache和16 Kb的shared memory时,所用的时间最短.原因在于48 Kb的cache和16 Kb的shared memory划分方式,可极大提高cache的命中率,同时在这种block维度下,单位时间内SM上所运行的实际线程为1 024,所使用的shared memory大小为15 Kb,这样不仅可充分利用SM的计算能力,还可充分利用shared memory.

3.2 算法的运行时间

文献[10]在GPU上实现了SPSO算法,在相同条件下,本文算法与文献[10]算法的对比结果列于表5～表7.

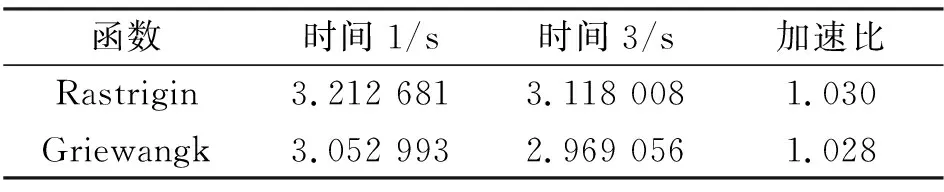
表5 Global memory优化结果Table 5 Performance of the optimization of global memory

表6 Register files优化结果Table 6 Performance of the optimization of register

表7 控制指令流优化结果Table 7 Performance of the optimization of control instructions stream

由表5～表7可见：

1) global memory上的优化实现并没有得到很好的结果.由算法1可知,完成数据拷贝后,SPSO算法由GPU完成.在数据依次拷贝中和拷贝后在CPU上进行的操作很少,异步传输的效果并不明显.

2) register上的优化实现没有得到很好的结果.因为计算中中间变量的使用是不可控制的.

3) 控制指令流的优化实现得到了很好的结果.因为算法1中步骤3)没有采用一个kernel函数里使用switch语句选择4个enchmark test函数的方式,而是编写了4个kernel函数,且控制流主要由CPU执行,GPU运行算法的并行部分,这样充分利用了GPU的并行性.

应用本文中的block维度选择和RAM划分情况,结合上述优化实现,最终的加速结果列于表8.在Rastrigin和Griewangk上运行SPSO算法与多核进行比较,加速结果列于表9.通过式(2),本文得到了1 000维的粒子， 时间结果列于表10.函数适应值(fitness)随迭代次数的变化情况列于表11和表12.

表8 最终优化结果Table 8 Final optimized results

表9 与多核的比较结果Table 9 Results of optimization compared with those by multi-core

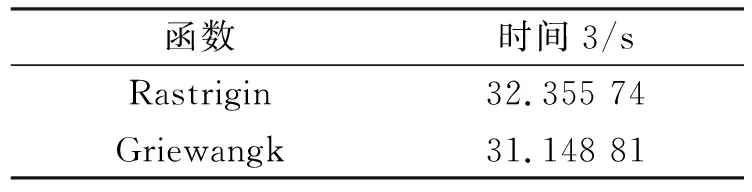
表10 Rastrigin和Griewangk所需时间比较结果Table 10 Time comparison results by Rastrigin and Griewangk

表11 Rastrigin的fitness随迭代的变化情况(N=2 000,D=50)Table 11 Fitness changes of Rastrigin function with iteration (N=2 000,D=50)

综上所述， 本文实现了Fermi架构上加速SPSO算法.首先,通过block的3种划分和shared memory的2种情况,衡量Fermi架构中SM的shared memory使用和SM的计算能力； 其次,在global memory 和register及指令流的使用上进行优化.实验结果表明,当block为16×8,shared memory为16 Kb,同时使用异步传输,减少并合并分支,最大限度使用register时,在函数f2上的加速比为1.579,在函数f3上的加速比为1.919.实验中实现了1 000维的粒子.

表12 Griewangk的fitness随迭代的变化情况(N=2 000,D=50)Table 12 Fitness changes of Griewangk function with iteration (N=2 000,D=50)

[1] Kennedy J,Eberhart R C.Particle Swarm Optimization [C]//Proc IEEE International Conference on Neural Networks.Piscataway: IEEE Press,1995: 1942-1948.

[2] Shayeghi A,Shayeghi H,Eimani K H.Application of PSO Technique for Seismic Control of Tall Building [J].International Journal of Electrical and Computer Engineering,2009,4(5): 293-300.

[3] Das M T,Dulger L C.Signature Verification (SV) Toolbox: Application of PSO-NN [J].Engineering Applications of Artificial Intelligence,2009,22(4/5): 688-694.

[4] FANG Hong-qing,CHEN Long,SHEN Zu-yi.Application of an Improved PSO Algorithm to Optimal Tuning of PID Gains for Water Turbine Governor [J].Energy Conversion and Management,2011,52(4): 1763-1770.

[5] Bratton D,Kennedy J.Defining a Standard for Particle Swarm Optimization [C]//IEEE Swarm Intelligence Symposium.Piscataway: IEEE Press,2007: 120-127.

[6] Mussi L,Daolio F,Cagnoni S.Evaluation of Parallel Particle Swarm Optimization Algorithms within the CUDA Architecture [J].Information Sciences,2011,181(20): 4642-4657.

[7] Weber R,Gothandaraman A,Hinde R J,et al.Comparing Hardware Accelerators in Scientific Applications: A Case Study [J].IEEE Transactions on Parallel and Distributed Systems,2011,22(1): 58-68.

[8] NVIDIA Corporation.CUDA Programming Guide for CUDA Toolkit 3.2 [EB/OL].[2012-03-08].http://developer.download.nvidia.com/compute/cuda/3\_2\_prod/toolkit/docs/CUDA\_C\_Programming\_Guide.pdf.

[9] Veronese L P,De,Krohling R A.Swarm’s Flight: Accelerating the Particles Using C-CUDA [C]//Proc IEEE Congress on Evolutionary Computation (CEC 2009).Piscataway: IEEE Press,2009: 3264-3270.

[10] ZHOU You,TAN Ying.GPU-Based Parallel Particle Swarm Optimization [C]//Proc IEEE Congress on Evolutionary Computation (CEC 2009).Piscataway: IEEE Press,2009: 1493-1500.

[11] NVIDIA Corporation.Whitepaper: NVIDIA’s Next Generation CUDA Compute Architecture: Fermi [EB/OL].2009-09-01.http://www.nvidia.com/object/fermi\_architecture.html.