基于分形维数和小波域特征的计算机生成图像检测算法

孙 利,齐嘉锐,李岩波,万国富

(1.吉林广播电视大学,长春 130022； 2.吉林大学 软件学院， 长春 130012；3.吉林大学 数学学院， 长春 130012； 4.吉林大学 计算机科学与技术学院,长春 130012)

自然图像是指利用数码相机拍摄得到的且未进行过任何篡改操作的照片图像.计算机生成图像是指利用计算机生成软件绘制生成的图像.自然图像没有经过任何篡改操作,是原始场景的真实写照,是真实图像.计算机生成图像是人们利用各种计算机技术而获得的图像,违背真实场景,因此计算机生成图像是假的图像.例如图1所示的自然图像与计算机生成图像,根据肉眼无法识别其真伪,因此只能从图像的内部特征提取而进行区分.

随着计算机技术的不断发展,数字图像篡改技术不断进步,人们可以使用计算机软件绘制出逼真的场景图像,以致凭感官无法识别其真伪,使图像的真实性面临巨大挑战.针对上述问题,目前已有许多检测算法,例如: Ianeva等[1]利用空间域特征(如亮度、 饱和度和HSV颜色直方图等)提取图像特征检测卡通图片,但该算法不能有效用于检测3D软件生成的JPEG图片;Lyu等[2]通过对图像进行小波变换分解,提取其一阶和高阶小波系数作为统计量对两种图像进行区分,对自然图像的检测率达到67%,但该算法没有从原理上指出计算机生成图像和自然图像的本质区别;姚丹红等[3]利用分形维数进行计算机生成图像检测,但该算法检测效果并不理想;Farid[4]利用小波域空间分析小波系数及其预测误差的高阶统计量,采用FLD线性分类器对自然图像和计算机生成图像进行训练,但实验效果也不理想;陈香苹等[5]利用空间域和变换域的特征作为统计量进行计算机生成图像的检测,相比于Farid等的方法已经有了一些改进,但实验效果依然不理想.除上述方法外,还有一些基于统计量的其他方法[6-7].

本文提出一种利用分形维数和小波域特征相结合的方法对自然图像和计算机生成图像进行检测：将所有待检测图像分为训练和测试两部分.首先对样本图像进行分形维数特征和小波域特征的提取;然后将分形维数的特征和小波域特征组合,作为整个算法的高维分类特征,形成一个高阶的特征向量;再用SVM分类器训练样本;最后使用SVM分类器对测试图像进行测试.算法流程如图2所示.实验结果表明,本文算法检测自然图像和计算机生成图像的效果较理想.

图2 算法流程Fig.2 Framework of the algorithm

1 分形维数特征提取

1.1 图像块筛选

文献[8]的检测方法中没有进行图像块筛选,直接对所有的图像块求取分形维数,因此检测效果并不理想.本文采用先进行图像块筛选得到感兴趣的图像块,然后进行分形维数特征提取的方法.

图像块筛选流程如下：

1) 将要输入的图像灰度化；

2) 将灰度化的图像分成大小为K×K的若干图像块(如K=128)；

3) 计算各图像块的方差；

4) 确定筛选图像块的阈值,该阈值主要由实验数据和相关经验确定,本文筛选图像块阈值设置为1 000；

5) 将图像块方差与阈值进行比较,如果该图像块的方差大于阈值,则认为该图像块是感兴趣图像块,保留该感兴趣图像块并用于分形维数计算;如果该图像块的方差小于阈值,则认为该图像块像素变化平缓,丢弃该图像块.

按照上述方法,可得到需要进行分形维数特征提取的所有感兴趣图像块.

1.2 分形维数计算

分形是一种具有自相似特性的现象、 图像或物理过程,即局部特性和整体特性是相似的.用“维数”表示某个现象、 图像或物理过程的不规则性和复杂性.

分形维数计算方法很多,本文采用“盒子”维算法[9],其算法流程如下：

1) 将得到的感兴趣图像块(大小为K×K)考虑成一个三维空间,坐标(x,y)表示二维坐标平面,用于标记像素位置,图像的灰度值表示Z轴方向;

2) 将二维平面(x,y)分成大小为l×l的若干格子(l为整数,且1≤l≤K/2),并令r=1/K;

3) 在每个格子中有许多体积为l×l×l的小盒子堆砌,使第(i,j)个格子中灰度表面的最大值和最小值分别落入堆砌序号(自下而上)为p和q的盒子中;

4) 令

nr(i,j)=p-q+1,

(1)

对所有的格子nr(i,j)求和,得

(2)

5) 用最小二乘法拟合lgNr-lg(1/r),求出的斜率即为盒子维数(dimension).

在“盒子”维算法中所有的立方体都放在固定的位置上,会出现立方体包裹不紧的情况,而对于l较大时,包裹不紧凑的情况更严重,会严重影响盒子的测量精度.因此本文算法将盒子数的计算方法修改为

nr(i,j)=(maxIk-minIk+1)/l.

(3)

该方法在盒子的计算过程中不再使用固定立方体的大小(l×l×l),而使用可变高度的长方体l×l×l′作为包裹曲面的盒子,这种方法对立方体的包裹更紧密,提高了分形维数的准确性.

2 小波域特征提取

本文针对由计算机3D软件生成的JPEG图像及由相机拍摄的JPEG图像进行检测,自然图像成像过程中所产生的噪声能在小波域上显示,所以在小波域上能区分计算机生成图像和自然图像.本文采用如下小波变换四镜像滤波器方法[4,7]:

1) 将输入图像灰度化；

2) 对该灰度图像进行n级小波分解,各级小波分解后的水平子带、 垂直子带和对角子带分别表示为Hi(x,y),Vi(x,y)和Di(x,y),其中i=1,2,…,n,表示第i级小波变换;

3) 对每个子带系数计算其高阶统计量,如均值、 方差、 偏度和峰度,得到一组特征,共12(n-1)维;

4) 利用线性误差预测器分别对水平子带、 垂直子带及对角子带的误差计算其高阶统计量,如均值、 方差、 偏度和峰度,得到第二组特征.

以垂直子带为例,一个线性预测器表示如下:

其中ωk为加权因子.这种线性关系可用如下矩阵形式表示：

V=Qω,

(5)

其中: 列向量ω=(ω1,ω2,…,ω7)T;向量V包含垂直子带小波系数的列向量;矩阵Q的每列由式(4)中相应的相邻系数组成.其二次误差函数定义如下：

E(ω)=(V-Qω)2,

(6)

该误差函数通过对ω求导数并令导数值为零使E(ω)达到最小值,因此可求出

ω=(QTQ)-1QTV,

(7)

则线性预测器的对数误差为

E=log2V-log2(Qω).

(8)

对E计算其均值、 方差、 偏度和峰度,该过程对于每级小波变换的垂直子带都重复一次,则每级小波变换的线性预测器也要重新估计一次.对于水平子带和对角子带,计算过程相似.水平子带的线性预测器形式如下：

对角子带的线性预测器形式如下：

线性误差预测器得到的均值、 方差、 偏度和峰度的特征维数为12(n-1),再结合小波子带系数统计量,则小波域特征共24(n-1)维,从而形成了一个特征向量,并可区分自然图像和计算机生成图像.

3 分类器的选择

由于分形维数和小波域特征相互组合而得到的高维特征通常是线性不可分的,SVM解决线性不可分问题效果较好,因此本文选择支持向量机(SVM)[10-12]作为算法的分类器.SVM的核心思想是对最优分类面的推广,即最大化不同类别间的分类间隔.SVM通常采用内积函数定义的非线性变换将输入空间转换到高维,使原来低维空间中线性不可分的问题变成高维线性可分,然后在高维空间中求解广义最优分类面问题.

假设xi(i=1,2,…,N)为特征向量,则分类器的目的是设计超平面g(x)=ωTx+ω0=0.其中:ω是超平面系数向量;x是输入向量;ω0是偏移量.与两类样本点距离最大的分类超平面会获得最佳的推广能力,即满足下式的最优分类超平面：

其中yi为+1和-1分别表示待分类的两类样本.假设λ1,λ2,…,λN是N个Lagrange乘子,K(xi,x)为映射核函数,则由式(11),(12)可得最终判别函数为

(13)

典型的核函数有线性核、 多项式核及RBF核等.在本文算法中,采用RBF核函数的C-SVC,即

K(xi,x)=exp(-γ‖xi-x‖2),

(14)

其中参数C和γ通过网格搜索获得最佳参数,搜索范围均为{2-5,2-4,…,25}.

4 实验结果

本文实验选择800张JPEG图片作为原始图片集,其中400张是自然图像,来源于哥伦比亚大学数字图像库,另外400张计算机生成图片主要来自3D图片网站.选择200张自然图像和200张计算机生成图像作为训练样本,另外的200张自然图像和200张计算机生成图像作为测试样本.实验步骤如下：

1) 读取一幅输入图像,同时得到其所属类别(Photorealastic Image=1,Computer Generated Image=-1);

2) 提取图像的分形维数特征;

3) 提取图像的小波域特征,对输入图像进行4层小波分解,可得到小波域共72维特征;

4) 重复1)～3),完成所有输入图像的特征提取;

5) 利用Libsvm中的easy.py进行交叉验证,寻找训练模式时的最优参数;

6) 利用步骤4)得到的图像特征与步骤5)得到的最优参数建立SVM模型;

7) 利用步骤6)得到的SVM模型对测试图像进行检测.

图3为实验检测阶段400张测试图片的检测结果,横坐标为400张测试图片的序号,纵坐标表示预测值,纵坐标为“1”表示自然图像,纵坐标为“-1”表示计算机生成图像,“●”表示实际值,“■”表示预测值.由图3可见,“●”与“■”的重叠部分表示预测正确的图片,孤立的“■”表示预测错误的图片.

图3 400张图片检测结果Fig.3 Detected results of 400 images

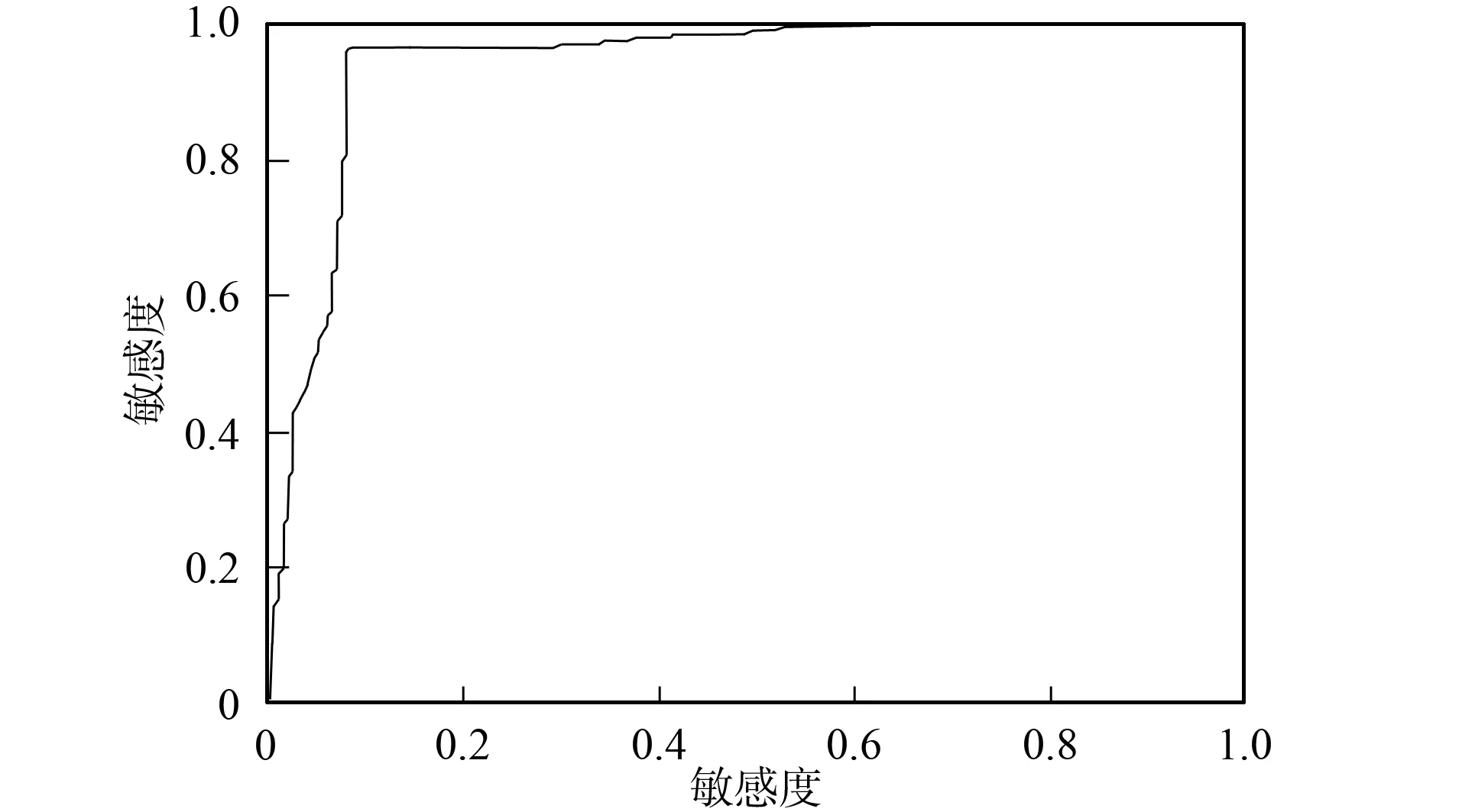
图4 ROC曲线Fig.4 ROC curve

图4为衡量上述400张图片预测结果的ROC(receive operating characteristic)曲线,ROC曲线下方面积用AUC表示,AUC越大,表示预测结果越精确,预测的理想结果是AUC=1.由图4可见,本文实验的AUC=0.943 0,是一个理想的数值.

表1列出了本文算法与文献[7]中检测准确率的对比结果,其中总检测准确率由自然图像检测准确率和计算机生成图像检测准确率的算术平均得到.由表1可见,本文算法对自然图像和计算机生成图像的检测准确率有较大提高.

表1 自然图像和计算机生成图像的检测准确率Table 1 Identifying accuracy of photographic and computer generated images

综上所述,本文提出了一种多特征结合的自然图像和计算机生成图像检测算法,先将分形维数特征和小波域提取的高阶统计量作为图像的统计特征,再利用SVM分类器对自然图像和计算机生成图像进行分类和检测.实验结果表明,本文算法对自然图像和计算机生成图像的检测准确率有很大提高.

[1] Ianeva T I,Vries A P,De,Rohrig H.Detecting Cartoons: A Case Study in Automatic Video-Genre Classification [C]//IEEE International Conference on Multimedia and Expo.Piscataway: IEEE Press,2003: 449-452.

[2] Lyu S,Farid H.How Realistic Is Photorealistic [J].IEEE Trans Signal Processing,2005,53(2): 845-850.

[3] YAO Dan-hong,SU Bo,LI Sheng-hong.Fractal-Dimension Based Algorithm to Detect Computer Graphics [J].Communications Technology,2008,41(12): 256-258.(姚丹红,苏波,李生红.基于分形维数的计算机生成图像检测方法 [J].通信技术,2008,41(12): 256-258.)

[4] Farid H.Detecting Hidden Messages Using Higher-Order Statistics Models [C]∥International Conference on Image Processing.Piscataway: IEEE Press,2002: 905-908.

[5] CHEN Xiang-ping,LI Sheng-hong,SU Bo,et al.Identifying Computer Generated Images Based on Analysis of Image Noise [J].Journal of Optoelectronics·Laser,2010,21(2): 293-297.(陈香苹,李生红,苏波,等.基于图像噪声分析的计算机生成图像检测算法 [J].光电子·激光,2010,21(2): 293-297.)

[6] ZHANG Zhen,REN Yuan,PING Xi-jian.Distinguishing Computer Graphics from Nature Image on Interpolation Algorithms [J].Journal of Geomatics Science and Technology,2009,26(4): 288-291.(张震,任远,平西建.基于插值算法的真实图像与计算机生成图像鉴别 [J].测绘科学技术学报,2009,26(4): 288-291.)

[7] WANG Yu-ping,LI Sheng-hong,ZHAO Feng,et al.Detection of Photorealistic Computer Graphic Based on AdaBoost [J].Computer Simulation,2008,25(7): 220-222.(王玉平,李生红,赵峰,等.基于AdaBoost的计算机生成图像检测算法 [J].计算机仿真,2008,25(7): 220-222.)

[8] Ng T T,Chang S F,Tsui M P.Physics-Motivated Features for Distinguishing Photographic Images and Computer Graphics [C]∥Proceedings of the 13th Annual ACM International Conference on Multimedia.New York: ACM,2005: 239-248.

[9] LIU Mei-hong,XU Wei-hong.Detection of Copy-Move Forgery Image Based on Fractal and Statistics [J].Journal of Computer Applications,2011,31(8): 2236-2239.(刘美红,徐蔚鸿.基于分形和统计的复制-粘贴篡改图像的检测 [J].计算机应用,2011,31(8): 2236-2239.)

[10] WANG Bo,KONG Xiang-wei,YOU Xin-gang,et al.Blind CFA Interpolation Detection Based on Covariance Matrix [J].Journal of Electronics &Information Technology,2009,31(5): 1175-1179.(王波,孔祥维,尤新刚,等.基于协方差矩阵的CFA插值盲检测算法 [J].电子与信息学报,2009,31(5): 1175-1179.)

[11] WANG Bo,KONG Xiang-wei,YOU Xin-gang,et al.Identification of Source Cameras Based on CFA Interpolation Algorithm Detection Using Covariance Matrix [J].Journal of Optoelectronics·Laser,2009,20(4): 517-520.(王波,孔祥维,尤新刚,等.利用协方差矩阵检测CFA插值的相机来源鉴别方法 [J].光电子·激光,2009,20(4): 517-520.)

[12] ZHANG Xue-gong.Introduction to Statistical Learning Theory and Support Vector Machines [J].Acta Automatica Sinica,2000,26(1): 32-42.(张学工.关于统计学习理论与支持向量机 [J].自动化学报,2000,26(1): 32-42.)