(2+1)维MKdV方程的Darboux变换及其孤子解

黄 坤,吕 悦

(1.华北水利水电大学 数学与信息科学学院,郑州 450011;2.吉林大学 数学学院,长春 130012)

1 (2+1)维MKdV方程

求解孤子方程的孤子解是非线性领域中的主要问题,目前已有许多求解孤子方程孤子解的方法,例如反散射方法、 双线性(Hirota)方法、 Bäcklund变换法、 Darboux变换法和代数几何法等.这些方法各有特点,也有内在联系.其中,Darboux变换是一种行之有效的方法,它从平凡解出发得到孤子方程的孤子解.

考虑(2+1)维MKdV方程的谱问题[1-3]:

(1)

其中:u=u(x,y,t)和v=v(x,y,t)是两个势;λ是一个谱参数.

解零曲率方程:

(2)

等价于解方程:

(3)

定义Lenard序列gj=(aj+2,2cj+2)T,由式(3)计算可得

假设方程(2)的辅谱问题为

(4)

(utn,vtn)T=Jgn,n≥1,

(5)

这里K,J是Lenard算子对,并满足Kgj-1=Jgj.当t0=y,t1=t时,由式(5)可解得两个(1+1)维MkdV方程:

设(u(x,y,t),v(x,y,t))是方程(6)和(7)的解,令w(x,y,t)=v2(x,y,t),则由方程(6)知

w∂-1uy=-(vvxx+u2v2+2v4),wx∂-1uy=-(2(vvxx)x-2vvxxx+2u2vvx+4v3vx),

代入方程(7)得(u(x,y,t),w(x,y,t)),即为如下(2+1)维MkdV方程的解:

(8)

方程(1)对应的辅谱问题为

φy=V1φ,φt=V2φ,

(9)

其中:

(2+1)维MKdV方程最初用于描述浅水中长波的扩散.近年来,越来越多的物理现象都可用其描述,如一维非线性Lattice波、 非线性电介质中电磁波与横向光学声子的相互作用、 在两个水平面上的瑞本对流、 非线性简谐振动及等离子体运动学中离子声波等.

2 Daboux变换

(10)

其中α,ak,bk,ck和dk(0≤k≤n-1)是关于x和t的函数.

由引理1的方法同理可证下列引理.

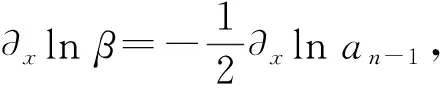
这里

其中β,ak,bk,ck和dk(0≤k≤n-1)是关于x和t的函数.

这里

其中γ,ak,bk,ck和dk(0≤k≤n-1)是关于x和t的函数.

当n=1时,3种Darboux变换有下列形式:

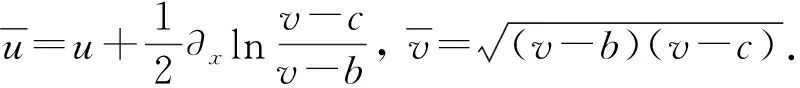
(14)

选取方程(1)中λ=λi(i=1,2)的两个基本解φ1=φ1(x,λ1),φ2=φ2(x,λ1),ψ1=ψ1(x,λ2),ψ2=ψ2(x,λ2),则有

γ(λ1+a)φ1+γbφ2=0,γ(λ2+a)ψ1+γbψ2=0,

γ-1cφ1+γ-1(λ1+d)φ2=0,γ-1cψ1+γ-1(λ2+d)ψ2=0,

计算得

(15)

其中Δ=φ1ψ2-φ2ψ1.

证明: 由关系

可得

同理可证方程(11),(12)其余各式成立.

3 3种Darboux变换间的关系

(2+1)维MKdV方程有3种Darboux变换,下面考虑n=1时,3种Darboux变换间的关系.

(16)

(17)

(18)

(19)

由上述关系,易得:

定理2若变量α,β,ai,bi,ci,di(i=1,2)满足式(16)～(19)的条件,则T2(λ2)·T1(λ1)=T,其中:

γ=αβa2,αβγd1=1,c1+c2=0;

(20)

a=(a1a2+b2c1)/a2,b=(b1a2+b2d1)/a2,c=(a1c2+d2c1)/d1,d=(b1c2+d2d1)/d1.

(21)

证明: 由式(16)～(19)计算可得

同理可证式(21)其余各式成立.

定理3当n=1时,若变量α,β,ai,bi,ci,di(i=1,2)满足下列条件:

(22)

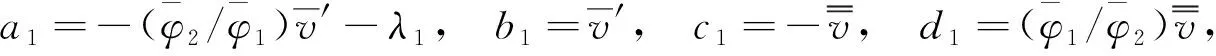
(23)

(24)

(25)

则可得3种Darboux变换间的关系：

T1(λ1)·T2(λ2)=T,

其中:

γ=αβa2;αβγd1=1;b1+b2=0;

(26)

a=(a1a2+b1c2)/a2;b=(a1b2+b1d2)/a2;c=(c1a2+d1c2)/d1;d=(b2c1+d1d2)/d1.

(27)

综合定理2和定理3可得T1(λ1)·T2(λ2)=T2(λ2)·T1(λ1).3种Darboux变换间的关系如下：

4 (2+1)维MKdV方程的孤子解

以平凡解u=0,v=-1作为种子解,代入Lax对问题(1)和(9)中,可得两个基本解为

参考文献[7-8],将上述两个基本解代入式(14)可得下列定理.

定理4当n=1,u=0,v=-1时,(2+1)维MKdV方程的孤子解为

(28)

其中:

(29)

当λ1>2,λ<-2时,两个孤子解u,v相互正碰,其平面图均沿x轴正向传播,如图1所示;当λ2>λ1>2 时,两个孤子解u,v相互追赶碰撞,其平面图均沿x轴负向传播； 当|λ1|<2,|λ2|<2时,两个孤子解u,v是周期解,如图2所示.

图1 (2+1)维MKdV方程相互正碰的孤子解Fig.1 Two-head-on collision soliton solution of (2+1) dimensional MKdV equation

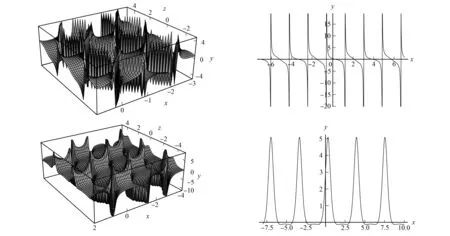
图2 (2+1)维MKdV方程的周期解Fig.2 Periodic solution of (2+1) dimensional MKdV equation

定理5当n=2,u=0,v=-1时,(2+1)维MKdV方程的孤子解为

u=-(lnd1)x,w=v2=(1+b1)(1+c1).

(30)

在λi>2或λi<-2(i=1,2,3)的范围内,当λi(i=1,2,3)同为负数时,孤子解u,w为3个孤子相互追赶碰撞,其平面图均沿x轴正向传播;当λi(i=1,2,3)同为正数时,孤子解u,w为3个孤子相互追赶碰撞,其平面图均沿x轴负向传播;当λi(i=1,2,3)两正一负或两负一正时,孤子解u,w是2个孤子追赶碰撞和1个孤子正碰,如图3所示.

图3 (2+1)维MKdV方程的3个孤子解Fig.3 Three-solitons solution of (2+1) dimensional MKdV equation

当n选取不同值时,利用3种Darboux变换T1,T2和T,可以得到(2+1)维MKdV方程更多不同的孤子解.

[1] CHEN Jin-bing.Algebro-Geometric Solutions to a Hierarchy of (1+1)-Dimensional and Two New (2+1)-Dimensional Nonlinear Evolution Equations [J].Chaos,Solitons and Fractals,2004,19(4): 905-918.

[2] CHEN Ai-hua,LI Xue-mei.Darboux Transformation and Soliton Solutions for Boussinesq-Burgers Equation [J].Chaos,Solitons and Fractals,2006,27(1): 43-49.

[3] GENG Xian-guo,HE Guo-liang.Darboux Transformation and Explicit Solutions for the Satsuma-Hirota Coupled Equation [J].Applied Mathematics and Computation,2010,216(9): 2628-2634.

[4] LIU Ping,ZHANG Jin-shun.Darboux Transformation of Broer-Kaup System and Its Odd-Soliton Solutions [J].Journal of Southwest China Normal University: Natural Science,2006,31(5): 31-36.

[5] HUANG Kun,CHEN You-jun.Relationship among the Three Kinds of Darboux Transformation and Explicit Solutions of Broer-Kaup System [J].Journal of Zhengzhou University: Natural Science Edition,2012,44(3): 38-41.(黄坤,陈友军.Broer-Kaup系统3类达布变换间的关系及其精确解 [J].郑州大学学报: 理学版,2012,44(3): 38-41.)

[6] LI Yi-shen,Zhang J E.Darboux Transformations of Classical Boussinesq System and Its Multi-soliton Solutions [J].Phys Lett A,2001,284(6): 253-258.

[7] ZHANG Jin-shun,WU Yong-tang,LI Xue-mei.Quasi-periodic Solution of the (2+1)-Dimensional Boussi Nesq-Burgers Soliton Equation [J].Phy A: Statistical Mechanics and Its Applications,2003,319(1): 213-232.

[8] WANG Zheng-yan,YANG Xiao.Explicit Solutions for a (2+1)-Dimensional Toda Lattice with Two Discrete Variable [J].Commun Theor Phys,2007,48(10): 667-670.