一类求解非线性方程最优的8阶收敛迭代法

王晓锋,张 铁

(1.东北大学 理学院,沈阳 110819;2.渤海大学 数理学院,辽宁 锦州 121013)

0 引 言

非线性方程求根问题是一个经典问题.近年来,对求解非线性方程迭代法的研究又一次成为热点,涌现出许多具有高计算效率和高收敛阶数的迭代法.在这些方法中,牛顿法(NM) 是最具代表性的迭代法[1],其格式如下：

(1)

定义1[2]设p为迭代法收敛的阶数,n为每次迭代过程中需计算的函数值总数,则迭代法的效率指数为p1/n.

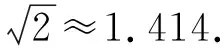
牛顿法具有最优收敛阶数2.在迭代步数相同的条件下,具有最优阶的迭代法计算成本较低,因此本文通过权函数方法构造一类新的三步最优的8阶收敛迭代法.

1 新的8阶收敛迭代法及收敛性分析

构造格式如下：

(2)

其中:

G(sn),L(sn),H(tn)和K(qn)是4个权函数.

定理1设函数f(x),G(x),L(x),H(x)和K(x)足够光滑,a∈I为函数f(x)在区间I上的单零点.若初始值x0在a附近选取,且权函数G(x),L(x),H(x)和K(x)满足下列条件：

(3)

则迭代法(2)是8阶收敛的.

证明：设第n步迭代误差为

利用Taylor展式将函数f(x)在零点a处展开,并令x=xn,可得

(4)

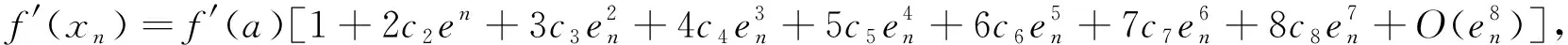
(5)

与式(5)类似,利用Taylor展式,将函数f(x)在零点a处展开,并令x=yn,可得

(7)

将权函数G(sn)在零点Taylor展开,可得

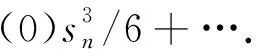
(8)

由式(2)～(8),可得

再将函数f(x)在零点a处展开,并令x=zn,可得

(10)

将权函数L(sn),H(tn)和K(qn)在零点Taylor展开,并假设|K‴(0)|<+∞,|H″(0)|<+∞,|L‴(0)|<+∞,可得

利用式(2)～(13),可得新迭代法所满足的误差表达式为

证毕.

定理1给出了新迭代法(2)具有最优收敛阶数8时权函数所满足的条件.由定理1可知,新迭代法的收敛阶为8,且该方法在每次迭代过程中需要计算3个函数值和1个一阶导数值,因此该方法效率指数为81/4≈1.682.选择适当的权函数使其满足定理1的条件,可得到多种迭代格式.这里给出如下两种迭代格式.

方法Ⅰ:

(15)

方法Ⅱ：

(16)

2 数值结果

下面举例验证本文迭代法的收敛性,将得到的最优8阶收敛迭代法(M8-(15)和M8-(16))与牛顿迭代法(NM)、 文献[4]提出的4阶收敛方法(K4)、 文献[7]提出的6阶收敛方法(ON1)和文献[9]提出的7阶收敛方法(N1)进行比较,数值结果列于表1和表2.实验运行环境为Windows XP,Matlab 7.0编程.其中:x0为初始值;a为非线性方程的根;|xk-a|(k=1,2,3)为绝对误差的绝对值;|f(xn)|为最后一次迭代所得近似解函数值的绝对值;ρ为收敛阶数[5].计算公式为

(17)

数值试验中使用如下3个测试函数：

1)f1(x)=x5+x4+4x2-15,a≈1.347 428 098 968 305 0,x0=1.6;

2)f2(x)=xex2-sin2x+3cosx+5,a≈-1.207 647 827 130 918 9,x0=-1.3;

3)f3(x)=ln(x2+x+2)-x+1,a≈4.152 590 736 757 158 3,x0=4.5.

表1 函数fi(x)(i=1,2,3)的数值结果Table 1 Numerical results for fi(x)(i=1,2,3)

由表1可见,新方法(M8)具有最优收敛阶数8,计算精度明显高于其他方法.由表2可见,迭代法(ON1)虽然收敛阶数较高,但其计算精度最低,原因在于其计算成本较高.在相同计算成本条件下(表2中函数值和导数值计算个数之和为12),本文新方法的计算精度和收敛速度明显好于其他方法.此外,新方法(M8)的效率指数为81/4≈1.682,明显高于牛顿法(NM)的效率指数21/2≈1.414、 文献[4]方法(K4)的效率指数41/3≈1.587、 文献[7]方法(ON1)的效率指数61/6≈1.348和文献[9]方法(N1)的效率指数71/4≈1.627.数值结果进一步验证了定理1的正确性.因此,本文的新方法是高效的.

综上,本文构造了一类用于求解非线性方程单根的最优8阶收敛迭代法,证明了新方法的收敛性,并通过数值实验进行了验证.结果表明,新方法计算精度高,收敛速度快,适合高精度计算.但新方法对初始值要求较苛刻,当初始值距离方程的根较近时迭代法收敛速度较快,反之,当初始值距离方程的根较远时迭代法收敛速度较慢,甚至不收敛.

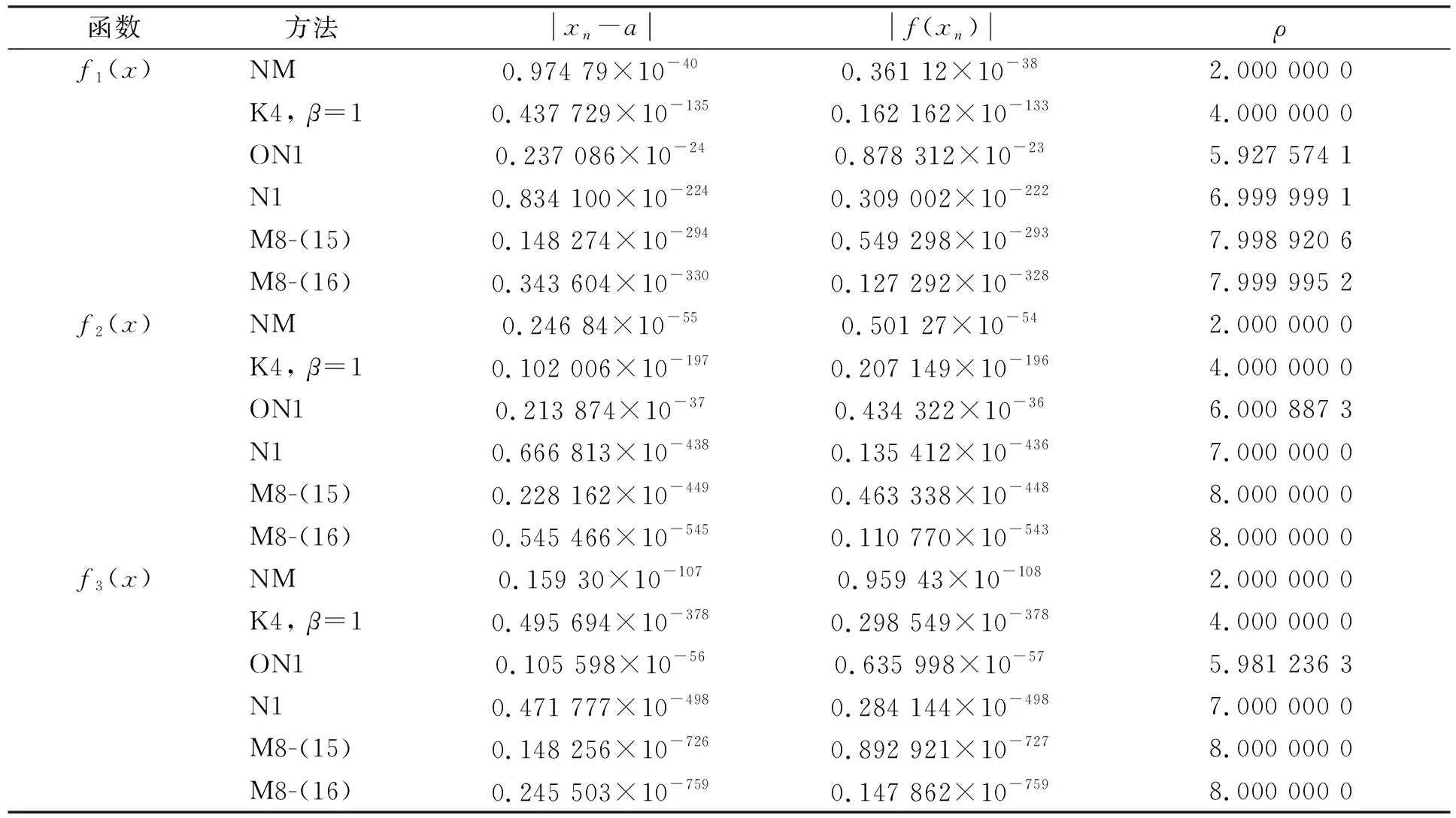
表2 不同迭代法的数值结果比较*Table 2 Comparison of numerical results for various iterative methods

* 所有的迭代法均具有相同的函数计算个数12.

[1] Kung H T,Traub J F.Optimal Order of One-Point and Multipoint Iterations [J].J Appl Comput Math,1974,21(4): 643-651.

[2] Ostrowski A M.Solutions of Equations and Systems of Equations [M].New York: Academic Press,1960.

[3] Ortega J M,Rheinbolt W C.Iterative Solution of Nonlinear Equations in Several Variables [M].New York: Academic Press,1970.

[4] King R F.A Family of Fourth Order Methods for Nonlinear Equations [J].SIAM J Numer Anal,1973,10(5): 876-879.

[5] Cordero A,Torregrosa J R.Variants of Newton’s Method Using Fifth-Order Quadrature Formulas [J].Appl Math Comput,2007,190(1): 686-698.

[6] WANG Xiao-feng,ZHANG Tie.A Family of Steffensen Type Methods with Seventh-Order Convergence [J].Numer Algor,2013,62(3): 429-444.

[7] WANG Xiao-feng,CHEN Jing.Variants of Newton’s Iteration Method with Sixth-Order Convergence [J].Journal of Henan Normal University: Natural Science,2010,38(4): 26-28.(王晓锋,陈静.6阶收敛的牛顿迭代修正格式 [J].河南师范大学学报: 自然科学版,2010,38(4): 26-28.)

[8] WANG Xiao-feng.Variants of Newton’s Iteration Method with Third-Order Convergence [J].Mathematics in Practice and Theory,2010,40(3): 216-218.(王晓锋.修正的三阶收敛的牛顿迭代法 [J].数学的实践与认识,2010,40(3): 216-218.)

[9] LIU Ya-mei,WANG Xia.A New Family of Seventh-Order Methods for Solving Non-linear Equations [J].Mathematics in Practice and Theory,2011,41(14): 239-245.(刘雅妹,王霞.一类新的求解非线性方程的七阶方法 [J].数学的实践与认识,2011,41(14): 239-245.)