基于马尔可夫链的体能训练质量评价*

汪名杰， 张 政

(装甲兵学院参谋系，安徽 蚌埠 233050)

基于马尔可夫链的体能训练质量评价*

汪名杰， 张 政

(装甲兵学院参谋系，安徽 蚌埠 233050)

介绍了马尔可夫链理论，探讨了马尔可夫链理论在体能训练质量评价中的应用.通过建模、实例阐述了该应用的方法及步骤,为体能训练质量评价提供了一种较为客观的方法，对于提高体能训练水平具有积极的意义.

马尔可夫链；体能训练；评价

平均成绩是传统体能训练质量评价的依据，这种方法重结果、轻过程，不能够客观准确地反映训练指导水平.以一个教学班来说，由于学员的体能基础不一样，经过一段时间的训练虽然得到了提高，但是如果用平均成绩来衡量这个教学班的训练质量，往往不能全面、细致地反映学员身体素质的提高情况.可见，传统体能训练质量评价方法容易影响考核的客观性和公正性，挫伤学员体能训练的积极性.为了准确反映学员的体能素质在一定基础上提高的程度以及未来的发展趋势，本文将采用马尔可夫链理论评价体能训练质量.

1 马尔可夫链的理论简介[1]

1.1马尔可夫过程

一个随机过程(xn,n=0,1,2,…)是一组随机变量，xn能取的各个不同的值，称为状态.如果一个随机过程(xn,n=0,1,2,…)，由一种状态转移到另一种状态的转移概率只与现在处于什么状态有关，而与在这时刻之前所处的状态完全无关，即如果过程(xn,n=0,1,2,…)中，xn+1的条件概率分布只依赖于xn的值，而与所有更前面的值相互独立，则该过程就是马尔可夫过程.

特别地，一个马尔可夫链，若从u时刻处于状态i，转移到t+u时刻处于状态j的转移概率与转移的起始时间u无关，则称之为齐次马尔可夫链(简称齐次马氏链).

1.2转移概率矩阵

如果把从状态i到状态j的一步转移概率记为pij，即pij=P{Xn+1=j|xn=i}(其中i，j=0,1,2,…)，则其构成转移概率矩阵如下：

1.3稳定状态矢量

设初始状态矢量为A(0)，则经一次转移得状态矢量A(1)=A(0)P.若为齐次马尔可夫链，则经二次转移状态矢量A(2)=A(1)P=A(0)P2，…，依次可推下去.对有限状态的不可约、非周期的齐次马尔可夫链，将会出现唯一的状态矢量A使A=AP成立，即状态矢量将达到稳定.这就是齐次马尔可夫链的遍历性.在应用中，若经判断发现A=AP有唯一解，即(E-P)A=0有唯一解，则此解就可以作为稳定状态矢量.

2 模型建立与评价思路

2.1模型建立[2]

为了便于评价，不妨以装甲兵学院本科学员的3 km成绩为例进行建模分析，将学员的3 km成绩分为四个级别：优秀，良好，合格，不合格，等级划分标准为优秀：12 min以内;良好：12～13 min；合格：13 min～13 min40 s；不合格：超过13 min40 s.

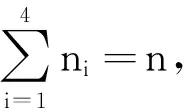
假设经过一段时间的体能训练后，进行第二次体能测试，在这段时间内，学员3km成绩转移情况可以用下面的转移矩阵来表示：

在上式中，nij(i,j=1,2,3,4)表示从状态i变为状态j的人数，P为转移概率矩阵.符合齐次马尔可夫链的体能状态转移概率矩阵的学员3 km成绩最后将趋于平衡状态X=(x1,x2,x3,x4)，即该教学班学员的第一次3 km测试结果对于其后的3 km测试结果几乎没有影响，但是学员的第一次3 km测试到第二次3 km测试之间的体能训练过程，以及根据该过程所确定的学员3 km成绩分布的变化情况，直接影响了后面的3 km测试成绩.

2.2评价思路

运用马尔可夫链理论进行体能训练质量评价的思路是[3,4]：首先，根据已知数据求出学员体能测试结果的状态转移概率矩阵P；然后，将状态转移概率矩阵P与其它已知条件联立建立一个方程组，求得学员体能成绩的稳定状态矢量；最后，结合权重进行综合计算，得到的结果就可以作为评价体能训练质量的依据.

3 评价实例

3.1数据采集

随机抽取本院某两个教学班(分别称为甲教学班、乙教学班)各30名学员,将体能训练前后两次3 km测试成绩的变化情况，按照马尔可夫链理论进行评价.这两个教学班的第一次和第二次的3 km测试成绩变化情况分别如表1和表2所示(已脱密处理).

表1 甲教学班学员3 km测试成绩变化情况

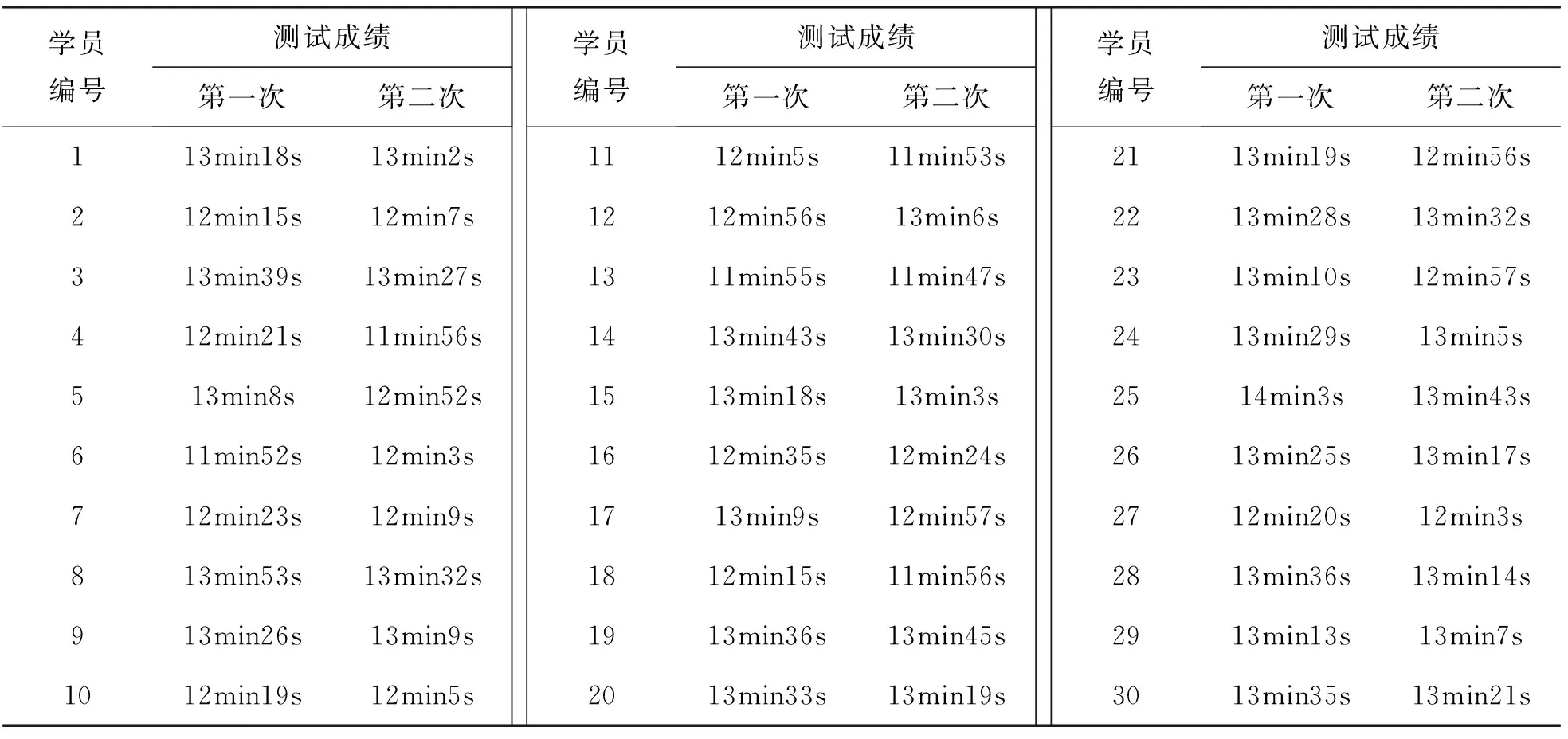
表2 乙教学班学员3km测试成绩变化情况

3.2数据计算

对表1和表2的数据进行分析，不难得到甲教学班学员的3 km成绩初始矢量和第二次测试成绩矢量分别为：

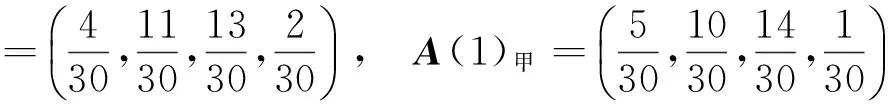
乙教学班学员的3 km成绩初始矢量和第二次测试成绩矢量分别为：

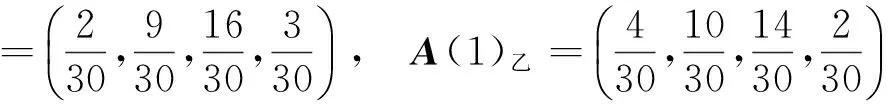
经过计算，可以得到甲、乙教学班学员的3km成绩的状态转移矩阵分别为：

甲、乙教学班3km成绩的稳定状态矢量分别为：

X甲=(0.235,0.324,0.382,0.059)，X乙=(0.310,0.465,0.207,0.018)

将学员的体能成绩四个级别优秀、良好、合格、不合格分别赋予权重为4、3、2、1，这样甲、乙两班的3 km综合评价成绩为2.735和3.067.

3.3结果分析

从A(0)甲与A(0)乙的比较来看，甲教学班学员的3 km体能基础要好于乙教学班.从A(1)甲与A(1)乙的比较得知，经过一段时间的训练后，两个教学班的成绩总体都有所进步，但是乙教学班学员的3 km成绩仍然不如甲教学班.这是通过传统求平均成绩的方法得出上述结论的.

但是，通过马尔可夫链理论得出的稳定状态矢量X甲和X乙来看，乙教学班学员的3 km成绩最终将超过甲教学班.也就是说，虽然乙教学班学员的3 km基础较差，但是如果两个教学班的体能训练方法和强度不变，继续按照这样的趋势发展下去，乙教学班学员的3 km绩最终将超过甲教学班，即乙教学班的3 km成绩由不如甲教学班变化为好于甲教学班，所以乙教学班的3 km体能训练质量好于甲教学班.而运用传统的求平均数的方法是无法得出上述结论的，可见，相对来说，马尔可夫链法更加客观、科学.

4 小结

本文针对体能训练质量评价所构建的马尔可夫链评价方法，充分利用了马尔可夫链中一步转移概率矩阵的基本特征，翔实、准确地从转移概率矩阵中得到了有规律变化的信息，建立的模型更加简单、合理和实用，对其它评价问题也具有较强的参考价值.当然，该方法也存在一定的局限性，影响体能测试结果的因素有很多，而不仅仅是体能训练.所以在实际运用该方法时，要具体情况具体分析，这样才能使评价结果合理、公正.

[1]陆大絟.随机过程及其应用[M].北京：清华大学出版社，2005:38-41.

[2]陈校平，车飞.装备保障能力的动态评估[J].火力与指挥控制,2011,36(7):167-170.

[3]刘焰余.基于马尔可夫链的启发式英语教学效果分析[J] .教学与管理，2013，(3):112-114.

[4]南峰.马尔可夫链模型在教学质量评价中的应用[J].河北理工大学学报,2005,5(2):127-130.

QualityEvaluationofPhysicalTrainingbasedonMarkovChains

WANG Ming-jie， ZHANG Zheng

(Staff Department, Armored Forces Institute, Bengbu Anhui 233050, China)

Markov Chains theory is introduced. Application of Markov Chains theory on physical training quality evaluation is discussed. The method and step is expounded through modeling and case. A relatively objective method of physical training quality evaluation is provided, which has positive significance for improving physical training level.

Markov Chains；physical training；evaluation

1673-2103(2013)05-0067-04

2013-10-23

汪名杰(1963-)，男，安徽怀宁人，副教授，硕士生导师，研究方向：应用数学.

O29；G812.5

A