关于函数连续性的再研究*

董立华

(德州学院数学科学学院， 山东 德州 253023)

关于函数连续性的再研究*

董立华

(德州学院数学科学学院， 山东 德州 253023)

指出函数连续与可导具有严格的一点对一点特征, 并通过实例说明确实存在着处处连续而处处不可导的函数. 其中函数的连续性、近似连续性、对称连续性均是对函数某点性质的刻画, 且容易证明函数连续一定对称连续,也是近似连续的, 反之不然.

函数连续; 对称连续; 近似连续

1 函数连续与可导

在数学分析中函数”可导必连续”的说法具有严格的一点对一点的特征,即函数在一点的可导性只能推出在该点的连续性而不能推及于其它点.例如,函数x2·D(x)在x=0点可导,同时仅在这一点连续. 一般来说，数学分析所讨论的连续函数在其绝大部分连续点上总是可导的，因此在数学分析的发展史上，数学家们一直猜测：连续函数在其定义区间中，至多除去可列个点外都是可导的. 也就是说，连续函数的不可导点至多是可列集. 但是，随着级数理论的发展，可以利用函数项级数构造处处连续而处处不可导的函数.

令：

显然hm→0(m→∞).当n≥m时,φ(10n(x+hm))=φ(10nx±10n-m)=φ(10nx);当nlt;m时,

上等式右端必定是整数,且其奇偶性与m一致,由此可知

不存在. 即该函数f(x)在R上处处连续而处处不可导.

2 函数的近似连续

数学分析中闭区间上的连续函数一定是黎曼可积的,而且积分也有连续性. 反之, 如果函数f(x)在闭区间[a,b]上黎曼可积, 那么f(x)的连续点在[a,b]中处处稠密, 即f(x)在[a,b]的每个子区间(c,d)中至少有一个连续点. 注意到，如果一个函数f(x)在[a,b]上的连续点不是处处稠密的，那么就可断言f(x)不是黎曼可积的. 例如函数：

但对于一个勒贝格可积的函数有下面的有关概念和结论.

定义1 设f(x)是定义在[a,b]上的函数,x0∈[a,b].假如存在可测集E⊂[a,b],使得x0是E之一全密点,即：

例如,函数f(x)在x=0点不是近似连续的. 其中

显然，由定义可知f(x)的连续点必是近似连续点.

容易证明, 勒贝格可积函数在它的每一个勒贝格点是近似连续的,其逆不真.反例如下: 设

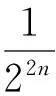
首先证明x=0是f(x)的右近似连续点.为此,令：

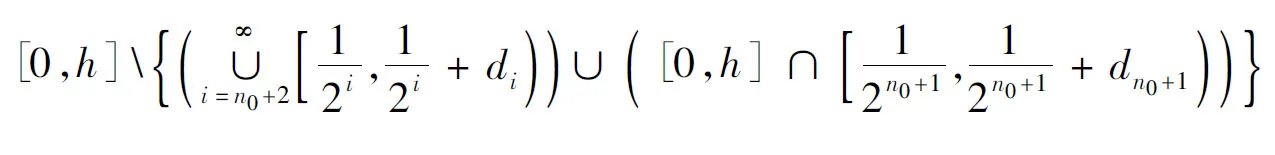
由此可知：

同理可证x=0是函数f(x)的左近似连续点. 因而x=0是f(x)的近似连续点.

即x=0不是f(x)的勒贝格点.

注:容易证明,对于有界可测函数而言, 勒贝格点与近似连续点相同. 上述反例说明了在这个陈述中, 函数有界的条件是不可去掉的.

3 函数的对称连续

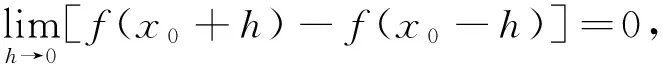
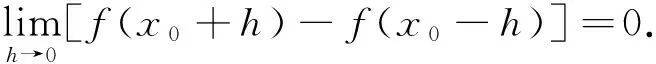
注:R上的每个对称连续函数必在R的某个稠密子集上连续. 还可进一步证明，对称连续函数必定是几乎处处连续的.

[1]陈纪修,於崇华,金路.数学分析[M].北京:高等教育出版社,2004.

[2]汪林.实分析中的反例[M].北京:高等教育出版社,1989.

ARestudyontheContinuityofFunctions

Dong Li-hua

(College of Mathematical Sciences, Dezhou University, Dezhou Shandong 253023,China)

The continuity and differentiability of functions possess the strict point to point character. By actual examples, we explain that there exist functions which are continuous but non differentiable everywhere. The continuity, approximate continuity and symmetric continuity describe the property of a point of functions. We also prove that, the continuity imply symmetric and approximate continuity, but not vice versa.

functions continuous; symmetric continuous; approximate continuous

1673-2103(2013)05-0005-03

2013-07-10

山东省“十二·五”教育科学规划项目(2011JG441)；德州学院教学改革研究重点项目(JGLX-A1108)

董立华(1965-)，女,山东平原人，教授，研究方向：函数论和教育管理.

O171

A