红细胞拉伸变形的粗粒化模拟

肖兰兰，陈 硕，刘俊彦，尚 智

（1.同济大学 航空航天与力学学院，上海200092；2.同济大学 汽车学院，上海201804；3.Institute of High Performance Computing，A＊STAR，Singapore 138632，Singapore）

人类血红细胞外表呈双凹圆盘形，其直径大约为8.0μm，中心最薄处厚度约为1.0μm.红细胞的主要功能是将肺吸进的氧运送到身体的其他组织，并带走呼出的CO2.人类血红细胞在其四个月的生命周期中，要成百万次地挤过细小的毛细血管，具有出色的变形性能［1］.红细胞膜由磷脂双分子层及附着在其内表面上的细胞骨架构成.细胞骨架对维持红细胞形状、膜的稳定和细胞的变形起着决定性的作用.细胞骨架主要由血影蛋白构成，这些血影蛋白通过短的肌动蛋白丝连接而形成网络状的膜骨架结构.

迄今为止，人们对红细胞力学特性进行了很多探索并获得了一系列实验、理论及数值模拟研究成果.实验方法包括微吸管法和光镊实验法等.实验观察表明红细胞在大变形时呈现出非线性变形特征.

理论模型主要分为两种：①连续介质模型；②微结构模型［2］.连续介质模型的优点是易于和基于连续介质的力学计算方法相结合，目前却不能够获得单个细胞变形的详细信息.微结构模型则试图详细地研究细胞变形与受力的关系，其中较为成功的有网络模型.网络模型认为细胞膜骨架是决定红细胞力学特性的主要结构，Boey等［3－4］提出了红细胞血影蛋白网络的三维网络模型.其所描述的单个红细胞变形模型得到了实验的验证，后来Li等［1］进一步对上述工作进行了扩展研究.然而，将Boey等［3－4］的红细胞模型运用到血液流动模拟中则需要巨大的计算量，目前还不可行.考虑到上述模型的缺陷，Pivkin等［5］基于平均场理论提出了一种红细胞模型的粗粒化方法.其三维红细胞膜模型考虑了弯曲能、面内剪切能，以及膜面积不变和由膜所包围的体积不变的约束，其成功之处在于可以将红细胞模型的自由度数量降低两个数量级，相应的计算量大为简化.在此基础上，Jiang等［6］对模型参数的影响进行了数值模拟及讨论.Fedosov等［7］在Pivkin等［5］工作的基础上，对红细胞血影蛋白分子网络模型的粗粒化模拟进行了系统的研究，提出了一套严格的粗粒化方法，在半分析理论的基础上，其所模拟的红细胞变形特性与前人光镊实验所得结果相吻合.

本文利用Gambit软件生成所需要的红细胞网络模型，对红细胞模型的粗粒化模拟进行讨论，包括构成细胞膜网络结构的粒子的受力分析、粗粒化参数的选取等.构成细胞骨架网络的非线性弹簧采用蠕虫链模型，弹簧受力采用指数模型.将上述粗粒化红细胞模型引入介观尺度数值模拟方法——耗散粒子动力学中，模拟由不同粒子个数构成的红细胞的变形特性，并与光镊拉伸实验值进行对比.讨论模拟参数对红细胞变形的影响，包括面积控制常数对红细胞面积和体积变化的影响，以及不同的指数和受拉伸的粒子个数对于红细胞拉伸变形的影响.

1 红细胞数值模型

1.1 红细胞膜的模型方程

前人实验表明，受到剪切作用而变形的红细胞，当剪切停止作用以后，红细胞将松弛并恢复为双凹形状，并且红细胞的边缘始终由膜的同一部分所组成，这说明红细胞的膜结构中储存有弹性能［5］.无应力状态下的红细胞呈双凹圆盘形，所储存的弹性能最小，其外形可表述为［8］

式中：细胞直径D0＝7.82μm，a0＝0.051 8，a1＝2.002 6，a2＝－4.491.

利用Gambit软件在式（1）所描述的红细胞膜表面生成非结构化网格，将其网格节点坐标导出并作为构成红细胞膜的粒子点坐标，如图1所示.网格节点之间的连接为蠕虫链连接，这些粒子坐标即为红细胞膜表面三角形网络的节点.

由上述节点所构成的红细胞膜结构系统的自由能可表述为［5，7］

式中：ri为粒子点的笛卡尔坐标，i＝1，…，Nv，Nv为构成红细胞膜的粒子个数.面内势能Ein－plane包括粒子之间的弹簧势能和细胞膜内其他弹性势能

式中：Ns为所有粒子点两两之间的弹簧连接的个数；Nt为三角形单元的个数；li为弹簧的长度，即弹性连接的两个粒子之间的距离；Ak是第k个三角形单元的面积，U是弹簧势能.另外，常数Cq和指数q与选择的模型有关.本文选用的模型是蠕虫链模型（WLC），它的弹簧势能可以表示成

式中：x＝l／lmax∈（0，1），lmax是最大弹簧长度，对于WLC模型，一般取为弹簧平衡长度l0的2.2 倍；p为弹簧驻留长度，它的大小与模拟所选用的粒子数有关；kB为玻尔兹曼常数；T为温度值，取296K.另外，式（3）中Cq在WLC模型中表达式为

式中：Kp为作用力系数，m为指数.WLC与POW 相结合可以形成指定的非零平衡长度的弹簧，文献［7］建议指数m取2来模拟红细胞非线性变形，这个模型被称为WLC－POW 模型.Kp的取值可以通过在弹簧处于平衡状态时面内作用力为零这一条件算出，即

本文的数值模拟也是在这个模型的基础上进行的.通过对面内势能求导，再加上式（6），就可以算出面内作用力的大小为

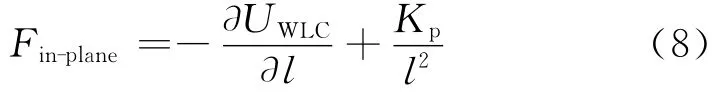
对于某一点o所受到的作用大小，其表达式如下：

式中：n为o点的弹簧连接个数，ro为o点的矢量坐标.

红细胞膜的弯曲势能定义为

式中：Kbend是弯曲常数，θi是具有共同边i的相邻两三角形单元α 和β 单位法向量之间的瞬时夹角，θ0是松弛状态下的夹角.其中cosθi＝nα·nβ，并且，当取“＋”时需满足（nα－nβ）·（rα－rβ）≥0.nα和nβ分别为两个三角形单元α 和β的外法线向量，rα和rβ分别为两个三角形单元的质心向量［9］.

o点的扰动不仅影响o点所在单元的弯曲势能，而且也会影响与其所在单元相邻单元的弯曲势能，如图2所示.因此将弯曲势能转化成o点的作用力为［10］

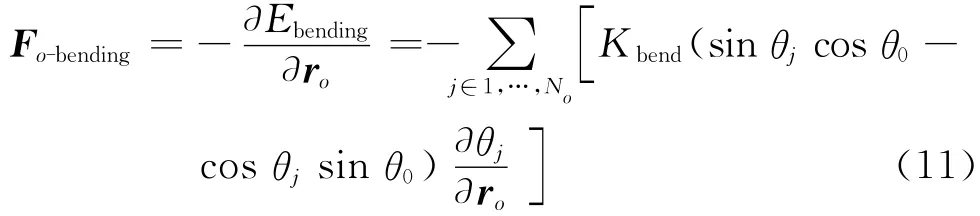
式中：No为o点所影响到的三角形单元的个数，θj是与o点有关的三角形单位法向量与其相邻三角形单位法向量之间的夹角.式（2）中的另外两项分别是面积控制势能Earea和体积控制势能Evolume.它们的表达式为

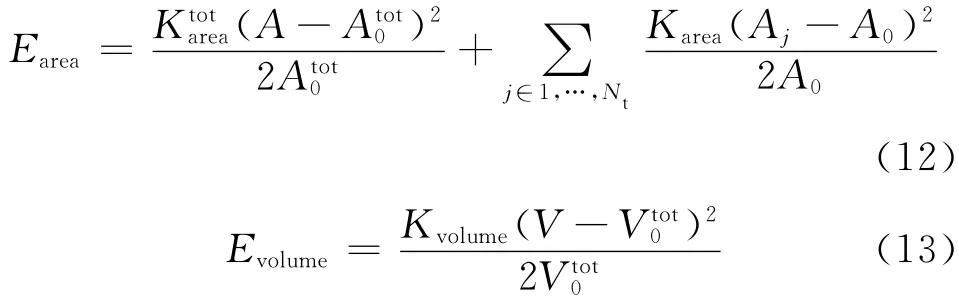
综合以上分析，可以得到某一粒子点o的作用力

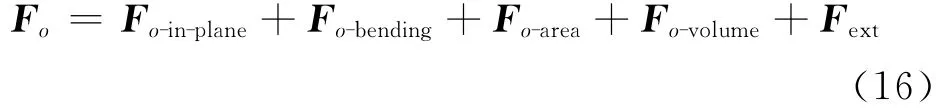
式中：Fext为o点所受到的外力.

1.2 粗粒化

红细胞的精细模型所需要的粒子数大约为27 000～45 000，模拟红细胞变形所需要的计算量较大，有必要引入粗粒化模型以减少计算量.根据Pivkin等［5］的研究，可以得到粗粒化模型参数与精细模型参数的转换关系为

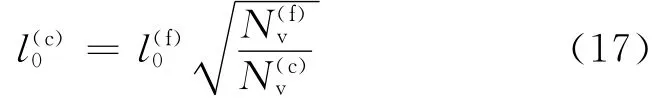
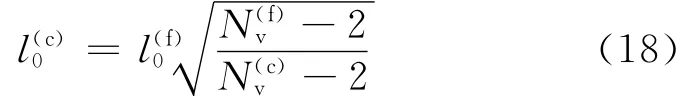
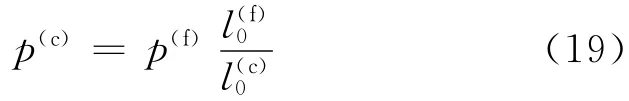
其中对于蠕虫链模型（WLC），p（f）＝14.68nm.根据弹簧最大长度lmax为平衡长度l0的2.2倍的关系，可得

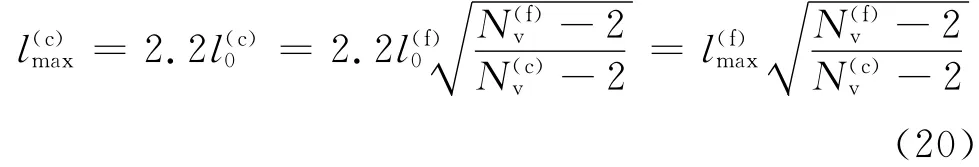
这样，通过式（18）～（20），在已假定红细胞粗粒化模型粒子点个数的前提下就可以计算出所需要改变的粗粒化模型的参数.

需要特别说明的是，Pivkin 等［5］的研究对单元之间松弛状态下的夹角也进行了粗粒化.

与上述处理不同的是，本文默认红细胞粗粒化网络模型生成后的单元夹角即为θ（c）0，它的大小与模型的粗粒化程度有关.

1.3 尺度缩放

数值模拟过程中，红细胞模型的粗粒化处理应保持红细胞的力学特性不变.模型中的量纲一参数与真实的物理参数之间需要建立对应关系，即应对物理量进行尺度缩放.

模型参数中的长度尺度［4］

式中：下标P和M 分别代表物理参数值和模拟参数值，D为红细胞直径.真实红细胞的平均直径DP＝7.8μm.

模型中的量纲一杨氏模量YM与国际单位制杨氏模量YP（N·m－1）之间的换算关系［7］为

式中：EM为模型参数中的单位能量，EP是国际单位制中的单位能量，即J.为使等号两侧单位一致，右侧需除以m2.由此可以得到模型参数中的单位能量的表达式［7］

如果rM取为1.0×10－6m，YP取为18.9×10－6N·m－1，YM根据文献［7］取为392.453，则EM的取值为

由此，可知式（4）中量纲一值kBT的计算为

进一步，模型参数中与真实参数单位力之间的转换关系为

其中FP的单位为N.其他参数的转换关系可由此类推.特别注意的是，式（24）和（25）对文献［7］中的公式做了补充说明.

2 红细胞的力学参数

为了保证膜的网络结构模型所预期的力学响应，必须选择一些力学参数，包括膜的弹性剪切模量μ0、压缩模量H及弯曲模量Kbend.根据实验测得红细胞膜的弹性剪切模量μ0 在4μN·m－1至12 μN·m－1之间.文献［11］中正六边形网络为单元推导出WLC－POW 模型的剪切模量

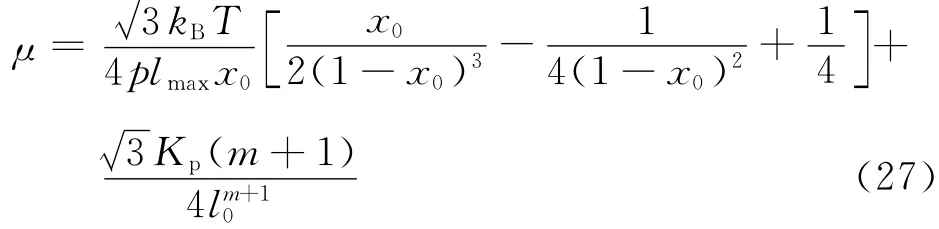
由较小的面积膨胀引起面内压力P改变，从而定义压缩模量［11］

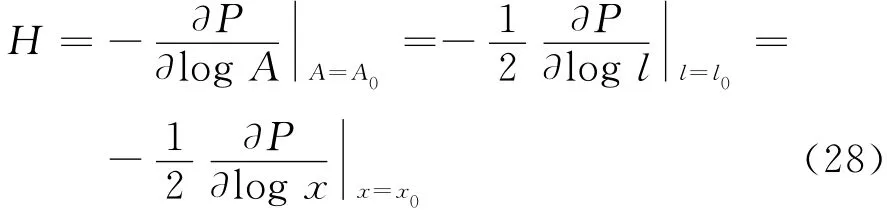
根据压缩模量方程可得WLC－POW 模型的压缩模量［7］

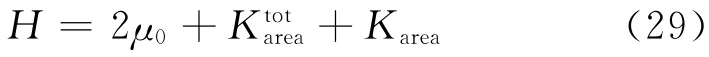
二维杨氏模量和泊松比［11］

红细胞膜的面积几乎不变，所以压缩模量远远大于弹性剪切模量.当H→∞时，可以得到Y→4μ0 以及ν→1.

从球壳的弯曲能分析中建立弯曲模量Kbend和宏观膜弯曲刚度Kc的关系，可得到弯曲模量为［7］

一般Kc的取值为2.4×10－19J.

3 模拟结果

3.1 红细胞拉伸测试

在完成模型建立之后，开始对红细胞进行拉伸模拟.首先要设定面积和体积控制常数，令Ktotarea＝4 900，Karea＝100，Kvolume＝5 000，而且对于弯曲常数Kbend，按照式（24）及（31）取值为5.754J.

接下来，把红细胞放在耗散（DPD）粒子中，并固定住它的中心点，在红细胞两端处红细胞总粒子数2%的粒子上加载拉力F，图3中红细胞两端黑色粒子为受拉伸的粒子.

先后对粒子数为191，519，1 048，2 512，5 253的红细胞进行拉伸，表1给出了粗粒化后的参数变动.表1中的数值是模型中使用的量纲一数值，对应的长度尺度rM为1.0×10－6m.另外，精细模型的驻留长度取为18.7×10－6m.

表1 红细胞模型粗粒化参数调整Tab.1 The parameter adjustment of coarse－grained RBC model

在同样的拉伸荷载下，不同粒子数目红细胞模型的变形如表2所示.表2中上面一排为不同粒子数下红细胞模型在无外力拉伸时的形态，当拉力到达100pN 时，不同粒子数的红细胞网络模型产生变形，如表2中下排所示.对红细胞施加0～200pN 的拉伸力，研究红细胞的直径变化与所受拉力大小的关系，并将不同粒子数红细胞模型的拉伸变形曲线与前人光镊实验曲线［12］进行对比，如图4所示.

图4中，上下两组曲线分别代表红细胞模型在拉伸时的最大直径Dmax和最小直径Dmin.计算表明红细胞粗粒化模拟的结果处于光镊实验值与精细模型模拟值之间.由计算结果可以看出，当构成细胞膜的粒子数粗粒化为191时，其变形依然与光镊实验值符合较好.不同粒子数所描述的红细胞在相同外力下拉伸变形有一定的差别，表明粗粒化有一定的影响.这在一定程度上与红细胞网络模型中三角形单元生成的质量好坏有关.文献［11］提出用一种称为“点电荷”的方法来生成红细胞网络节点，这种方法值得探讨.

?

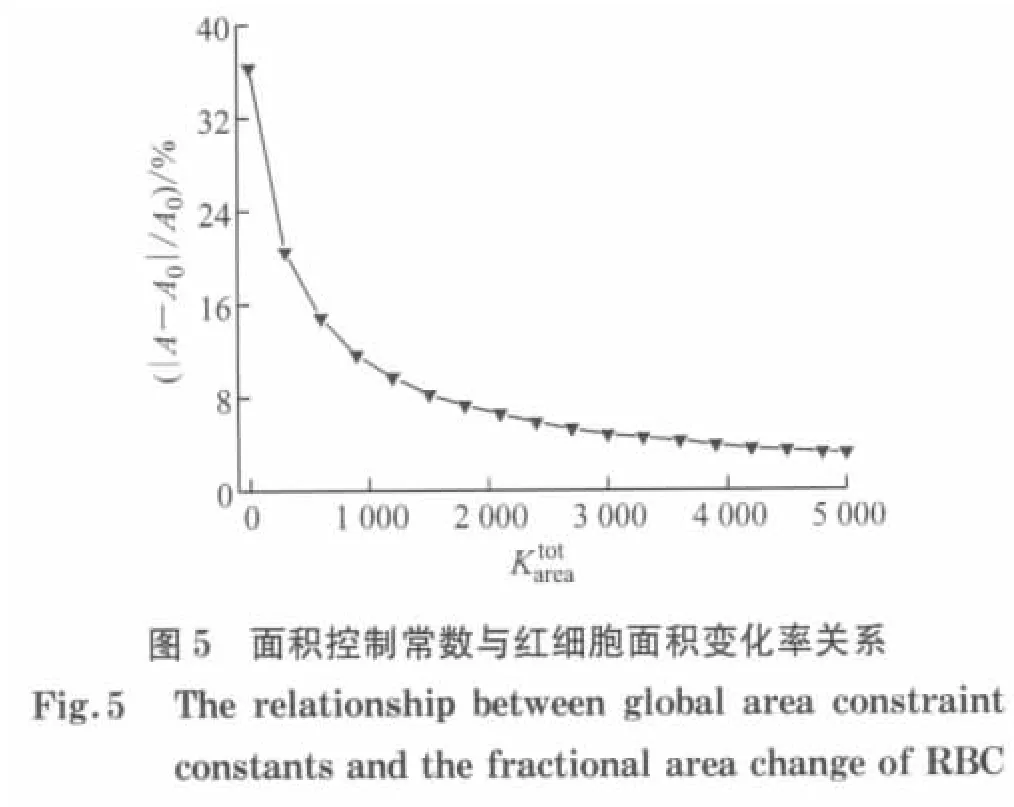
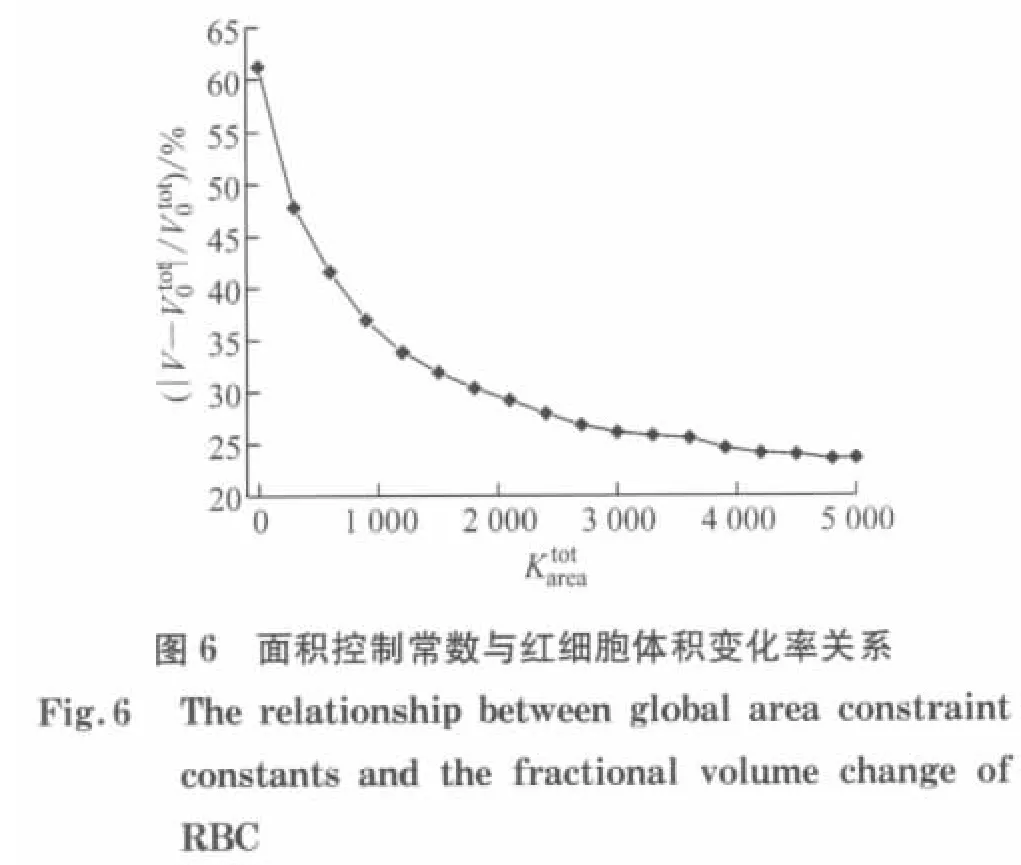
3.2 红细胞面积控制测试

本文所使用的模型假设红细胞膜是不可压缩的，由于红细胞膜的厚度很小，其变化不大，所以红细胞膜的面积几乎保持恒定，则根据式（29）压缩模量的表达式，当H→∞时，红细胞膜的面积完全不发生改变.由此可知面积控制常数远远大于膜弹性剪切模量μ0，为了使面积变化量不超过所限定的范围，需要调节面积控制常数.

3.3 指数m 和受拉伸粒子个数对拉伸变形的影响

当改变式（6）中的指数m时，粒子数为2 512的红细胞模型产生不同变形，如图7所示.图中m从1变化到3，在75pN 的拉力下红细胞的最大直径从13.25μm 变为12.39μm，这说明式（6）中指数的选择对于红细胞的变形有一定的影响.从拉伸结果看，当m＝2 时，拉伸结果曲线与光镊实验值曲线更加接近.

图7 不同的指数m 对红细胞变形的影响（N（c）v ＝2 512）Fig.7 The influence of different exponents m on the deformation of RBC

对粒子数为1 048的红细胞进行拉伸，改变受拉伸的粒子个数，发现产生不同的拉伸变形，如图8所示.在受拉伸粒子个数占构成红细胞粒子总数的2%的情况下更接近于光镊实验值，当受拉伸粒子数为5%时拉伸时其最大直径的变化偏离光镊实验值.

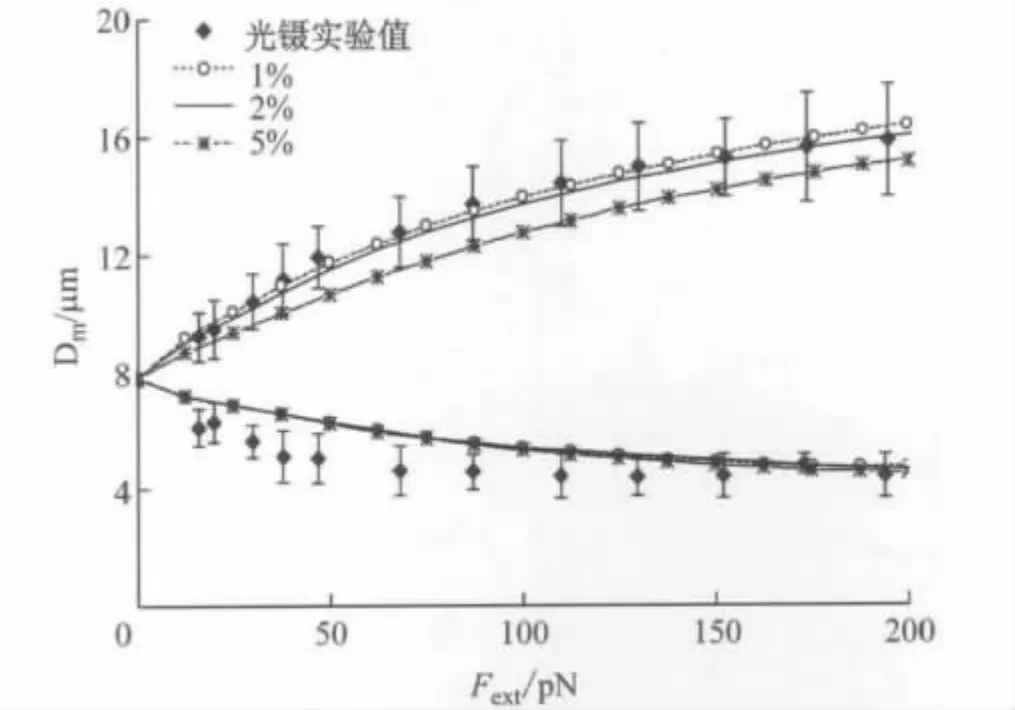
图8 不同受拉伸的粒子数对红细胞拉伸变形的影响（N（c）v ＝1 048）Fig.8 The comparison between the stretching response of RBC for different numbers of vertices subjected to the stretching force and the experiments

4 结语

本文采用蠕虫链模型进行了红细胞模型粗粒化模拟.对于模型中量纲一参数与真实物理量之间的对应关系进行了讨论，对于粒子点上的弯曲势能以及面积、体积势能所对应的受力进行了分析.模拟结果显示，当外力从0pN 变化到200pN 时，模拟结果与前人光镊实验较为一致，也是对文献［5，7］的验证.红细胞离散模型的粒子点生成，对于红细胞的变形性能有着较大的影响.为了模拟多个红细胞在血液流动中的变形，需要较少粒子数组成的红细胞模型，从而可以大大减少计算量，因此要寻求组成单个红细胞最少的粒子个数.红细胞的变形受模型中许多参数的影响，本文分析了面积控制常数对于红细胞表面积和体积变化的影响，从而选取合适的面积控制常数.指数和拉伸粒子个数对于红细胞拉伸变形的影响本文也进行了分析，可以看出影响红细胞模型变形的因素有很多.对于其他因素的影响分析将是今后的工作.此外，对于红细胞在血液流动中的变形，包括毛细血管中的泊潇叶流动中的变形、在剪切流中的变形以及多个红细胞在血液流动中发生的聚集行为等也将是进一步研究的内容.

［1］ Li J，Lykotrafitis G，Dao M，et al.Cytoskeletal dynamics of human erythrocyte［J］.Proceedings of the National Academy of Sciences，2007，104（12）：4937.

［2］ Hosseini S M，Feng J J.A particle－based model for the transport of erythrocytes in capillaries［J］. Chemical Engineering Science，2009，64（22）：4488.

［3］ Boey S K，Boal D H，Discher D E.Simulations of the erythrocyte cytoskeleton at large deformation.I.Microscopic models［J］.Biophysical Journal，1998，75（3）：1573.

［4］ Discher D E，Boal D H，Boey S K.Simulations of the erythrocyte cytoskeleton at large deformation.II.Micropipette aspiration［J］.Biophysical Journal，1998，75（3）：1584.

［5］ Pivkin I V，Karniadakis G E.Accurate coarse－grained modeling of red blood cells［J］.Physical Review Letters，2008，101（11）：118105.

［6］ Jiang L G，Wu H A，Zhou X Z，et al.Coarse－grained molecular dynamics simulation of a red blood Cell［J］.Chinese Physics Letters，2010，27（2）：028704.

［7］ Fedosov D A，Caswell B，Karniadakis G E.Systematic coarsegraining of spectrin－level red blood cell models［J］.Computer Methods in Applied Mechanics and Engineering，2010，199（29）：1937.

［8］ Evans E A，Skalak R.Mechanics and Thermodynamics of Biomembranes［M］.Boca Raton：CRC Press，Inc.，1980.

［9］ Li J，Dao M，Lim C T，et al.Spectrin－level modeling of the cytoskeleton and optical tweezers stretching of the erythrocyte［J］.Biophysical Journal，2005，88（5）：3707.

［10］ Computational hydrodynamics of capsules and biological cells［M］.［S.l.］：CRC Press，2010.

［11］ Dao M，Li J，Suresh S. Molecularly based analysis of deformation of spectrin network and human erythrocyte［J］.Materials Science and Engineering：C，2006，26（8）：1232.

［12］ Suresh S，Spatz J，Mills J P，et al.Connections between singlecell biomechanics and human disease states：gastrointestinal cancer and malaria［J］.Acta Biomaterialia，2005，1（1）：15.