海南近海Envisat测高波形重构海面高质量评价

赵 健，沈云中

（1.同济大学 测绘与地理信息学院，上海200092；2.中国石油大学（华东）地球科学与技术学院，山东 青岛266580；3.同济大学 空间信息科学及可持续发展应用中心，上海200092）

卫星测高技术能在全球范围内准确提供星下点瞬时平均海平面高度的观测值，在深海区域测得海面高（SSH）的精度可以达到±2～3cm.自1992年以来先后有T／P，ERS－1／2，GFO，Envisat，Jason－1／2等测高卫星曾经或仍然投入运行中，其观测数据被广泛应用于海平面变化、地球重力场、海底地形、海洋环流等方面的研究［1］.

目前卫星测高主要应用于深海区域，根据卫星测高数据的质量控制条件，离岸约20km 以内的近岸海域大部分数据因质量太差均被删除，导致近海测高数据不可用，但卫星测高在近岸海域的测量数据包含了大量有价值的信息.由于认识到近岸海域卫星测高数据的重要性，目前欧空局（ESA）的COASTALT 项目和法国宇航局（CNES）的PISTACH 项目正在进行中，旨在通过区域性的潮汐和大气逆压模型以及多颗卫星的轨道校正，研究和建立适用于近海的卫星测高数据处理方法，重新处理以往测高卫星在近海的历史数据，生成新的数据产品［2］.

Envisat是ESA 于2002 年3 月 发 射 的 太 阳 同步卫星，为ERS－1／2的后续卫星，其主要载荷之一为高度计RA2，轨道高度800km，轨道倾角98°，重复周期约35d，测量频率为Ku波段和S波段，在赤道上相邻轨道间隔约80km，18Hz测高波形数据对应地面轨迹采样点间距约为400m［3］.

1 波形重构算法

深海卫星测高回波波形遵循Brown海洋模型，因此可获得高精度的测高距离.近岸海域测高回波波形由于受陆地回波的污染，无法精确提供卫星与星下点之间的距离，影响到离岸约20km 的范围；而且近海的大气湿对流层校正、海洋潮汐校正及大气高频因数校正等校正量不准确，由此求得的距离包含较大的误差，甚至错误［4］.为了得到精确的测高距离观测值，必须对高度计原始波形数据重新处理，确定波形前缘中点的位置，对地球物理数据记录（GDR）中给出的卫星到海面的距离进行改正，该过程称为波形重构［5］.

近年来国内外许多学者对波形重构算法进行了大量研究.鲍李峰等［1］、杨乐等［4］分别利用Beta－5算法和重心偏移（OCOG）算法等对中国南海区域T／P和Jason－1卫星测高数据进行波形重构处理，用于近海海平面变化的研究.郭 金 运等［5－7］和Hwang等［8－9］提出了多子波参数重构算法，并对阈值（Threshold）算法进行改进，通过从有多个上升沿的回波中提取出子波形，再确定出与大地水准面模型最合适的海面高结果.

Envisat高度计RA2 发布的测高数据产品中SGDR 为传感器数据，它除了GDR 数据外，还包含离散傅里叶变换和快速傅里叶变换算法分别处理得到的18Hz波形数据.GDR 数据中不仅包含常规数据，还包 含 了Envisat利 用Ice－1，Ice－2，Sea－ice 和Ocean1等四种波形重构算法改正后的海面高，但没有给出四种结果的比较说明以及在非远海表面上测高结果的选取标准.Ice－1和Ice－2算法主要是针对冰面进行波形重构，Sea－ice算法针对海冰面回波进行波形重构，Ocean1算法是针对海洋面回波进行波形重构［5］.

为改善近海的卫星测高数据质量，本文对Envisat在海南近海的18 Hz测高波形数据采用Ocean1，Threshold，OCOG 和Beta－5参数拟合等算法进行重构分析，其中Threshold算法采用多个不同阈值进行对比.除常规的改善程度（IMP）值外，还利用重构后海面高中稳态海面地形及时变海面地形（高频噪声）的标准差等指标对重构海面高质量进行评价，选取适合海南近海的波形重构算法；对研究区域的交叉点处重构后海面高进行比对，以验证重构算法的有效性.

2 研究区域

海南位于中国最南端，是仅次于台湾岛的中国第二大岛.其北隔琼州海峡与广东的雷州半岛相望，西邻北部湾与越南相对，东北邻南海与台湾省相对，东南和南部在南海中与菲律宾、文莱和马来西亚为邻，周围还分布了包括南海诸岛在内的众多岛屿、暗礁、暗沙.海南岛海岸曲折，沿海的潮流主要受巴士海峡和巴林塘海峡传入的太平洋潮波的影响，加上岛屿与岛群地形的影响，使得潮流状况较为复杂.潮流性质、大小、方向及流动方式，因时因地而异，强弱流区相间.整个岸段包括不正规半日潮、不正规全日潮和正规全日潮等三种潮流性质，且兼有往复流和旋转流等各种运动形式，涨落潮流历时不等现象也很明显.海南岛沿岸潮差的基本特点是东部和南部潮差比较小，西部较大，西北部最大.

图1 经过研究区域的八条轨迹Fig.1 Eight passes of the study area

Envisat共有八条轨迹经过海南岛，分别为轨迹68，75，111，118，340，347，383，390，如 图1 所 示.选取第20 周期的八条轨迹作为研究对象，其中轨迹68，111，340，383为升轨，经由南海进入海南，其余四条轨迹为降轨，由海南陆地进入南海.八条轨迹在研究区域形成四个交叉点，编号为1～4.利用四种波形重构算法对八条轨迹的18Hz测高回波波形进行重构研究，其中阈值算法的阈值分别采用了10%，20%，30%，50%，并将重构结果与由EGM08模型计算得到的大地水准面高进行比对，通过计算IMP值（见式（1））、稳态海面地形及时变海面地形（高频噪声）的标准差等评价指标来判断重构结果的精度.考虑海南近海海况的复杂性，将重构海面高中稳态海面地形粗差超过±5m 及时变海面地形（高频噪声）粗差超过±1m 的数据剔除.

3 计算结果

为了评价不同重构算法的重构效果，重构后海面高的改善程度可通过计算重构前后的海面高与大地水准面高差值的标准差，即IMP值进行评价.IMP值的计算公式为［8－9］

式中：δraw为重构前海面高与大地水准面高差值的标准差，δretracked为重构后海面高与大地水准面高差值的标准差.若IMP 为负值，表明波形重构后海面高比重构前海面高的精度低.

表1给出了研究区域八条轨迹不同算法计算得到的海面高与EGM08大地水准面高差值的标准差（SD）及对应的IMP 值.其中，Ocean 算法结果由GDR 数据中重构前海面高计算得到，Ocean1结果由SGDR 数据中Ocean1算法重构后的18 Hz海面高计算得到.轨迹68计算范围为17.0°N～19.3°N，轨迹75为17.0°N～19.5°N，轨迹111 为17.0°N～18.2°N，轨迹118 为17.00°N～18.07°N，轨迹340为17.0°N～18.6°N，轨迹347为17.0°N～18.3°N，轨迹383 为17.0°N～18.3°N，轨迹390 为17.00°N～18.95°N.

从表1中可以看到，研究区域中八条轨迹不同算法重构海面高与EGM08大地水准面高差值的标准差（SD）差别较大，其中OCOG 算法标准差最大，这主要是由于该算法使用了全部波形数据，当波形位于海陆交汇处时，因为海岸地形、地球物理环境等影响，波形中含有较大的噪声.因此OCOG 算法一般用来为其他算法求定初始值.Beta－5 算法基于Brown平均脉冲反射模型，采样适当的参数函数对测高波形进行拟合，标准差较小，但在近岸海域测高回波波形较为复杂，导致该算法可能不收敛，重构成功率相对偏低.Ocean1 算法的重构效果较好，标准差比Beta－5算法要小，主要是因为该算法基于改进的Hayne模型，适合对海洋面回波进行重构［3］.在OCOG 算法基础上改进得到的Threshold算法标准差最小，八条轨迹利用Threshold算法计算得到的IMP值均大于其他算法求得的IMP值，表明在研究区域该算法的重构效果最好.这主要是因为Threshold算法对星下点地形变化较为敏感，如果定好一个较为准确的阈值，这种算法将获得一个较好的波形前缘中点.Deng［10］通过分析澳大利亚近海的卫星测高波形，建议在离岸0～5km 内，阈值因子采用30%；离岸超过5km，海洋回波是主要的波形，阈值因子采用50%.通过表1 中10%，20%，30%，50%四种阈值因子的计算结果比对，可以发现海南近岸海域测高波形重构时Threshold算法的阈值因子采用50%效果较好.

表1 八条轨迹波形重构结果对比表Tab.1 Statistics of waveform retracking of eight passes

除了IMP值外，还应考虑波形重构后海面高的平滑度，即相邻点的海面高之间的差值要小，不能产生大的突变，应保持良好的光滑性［10－11］.图2～5 是分别选取八条轨迹中的111，118，340，390利用四种重构算法重构后海面高与EGM08大地水准面高的比对，其中Threshold算法阈值为50%.从图中可以看出，利用Threshold 50%算法重构后的海面高最为平滑，且重构后海面高与大地水准面高更为相似，表明Threshold 50%算法是目前最适合该区域的重构算法.

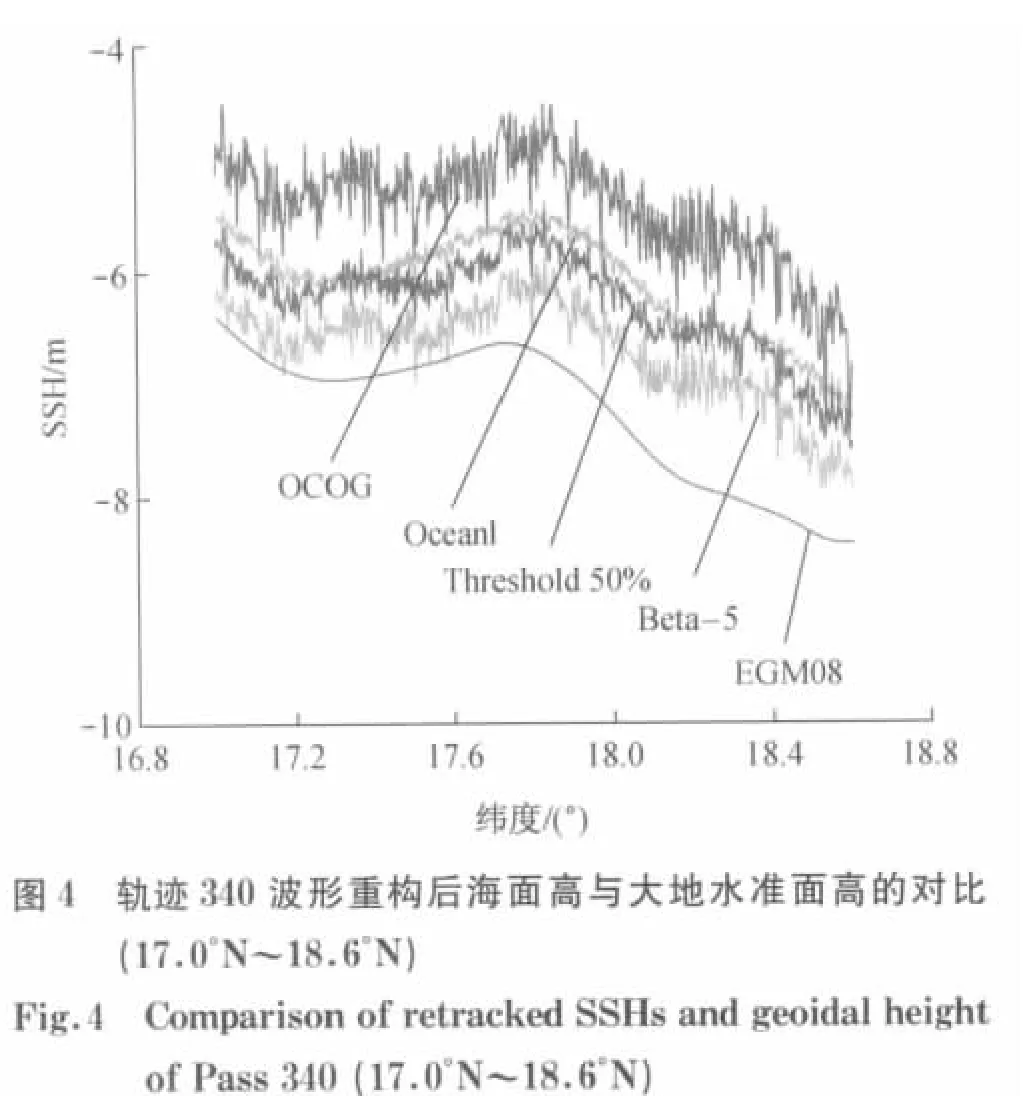
分析表1与图2～5可以发现，不同轨迹利用波形重构算法重构后海面高改善程度不同，重构前海面高的标准差对重构后的IMP值影响较大.四条降轨重构后海面高的改善程度均好于相邻的升轨，其中轨迹118波形重构效果最明显，重构后的IMP值达到59.0%.四条升轨重构前海面高标准差较小，此时测高波形多为海洋波形，未重构的海面高精度较高，因此重构后海面高改善效果不明显.四条升轨中轨迹340的IMP 值最大，为32.0%.而四条降轨重构前海面高标准差较大，此时测高波形多为似海洋波形，波形质量较差，未重构的海面高精度相对较低，重构后海面高的改善效果更为明显.除轨迹75之外，其余三条降轨重构后IMP 值均在40%以上.需要注意的是，当测高轨迹较短或研究区域较小时利用IMP值来评价重构算法的改善程度效果较好.由于海面地形变化的影响，较长轨迹或较大研究区域重构前海面高标准差可能会较大，但重构前后海面高标准差的差值可能会随着统计样本的增加而减小，使得IMP 值反而会较小，导致评价结果无法客观反映重构算法的改善情况.

重构海面高与大地水准面高之间的差值主要由两部分组成：一部分为稳态海面地形，主要为中长波分量；另一部分为时变海面地形（高频噪声），主要反映重构海面高的粗糙度.稳态海面地形的精度可利用大地水准面高与重构海面高每秒均值的差值来评价；时变海面地形的精度可通过18 Hz重构海面高与其每秒平均值之间的差值来评价［12］.以轨迹68为例，经过粗差剔除后，分别计算不同重构算法重构后的稳态海面地形与时变海面地形的标准差，如表2所示.表2中第二列为不同重构算法重构海面高中稳态海面地形的标准差（SST SD），第三列为重构海面高中时变海面地形（高频噪声）的标准差（Noise SD）.将研究区域八条轨迹重构海面高整体分析，考虑到海面地形的复杂性，在此仅计算不同重构算法重构后海面高中时变海面地形的标准差，结果如表3所示.从表2和表3中可以看出，无论是单条轨迹还是整个区域，Threshold 50%算法的标准差均较小，表现较为稳定，说明该算法是最适合该区域的重构算法.

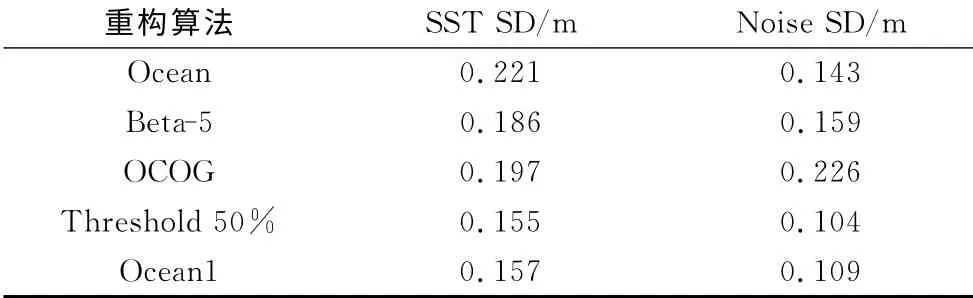
表2 轨迹68重构算法效果对比Tab.2 Comparison of retrackers of Pass 68

表3 研究区域重构算法效果对比Tab.3 Performance of retrackers in the test regions

研究区域内四条升轨与四条降轨形成四个交叉点，利用最为稳定的Threshold 50%算法、Ocean1算法分别计算升降轨在交叉点处的重构海面高，结果如表4所示.从表4中可以看到，同一交叉点处升降轨重构海面高结果非常一致，不符值为1～3cm.交叉点海面高计算结果验证了重构算法的有效性，说明在近岸海域进行波形重构是非常必要的，可显著提高卫星测高数据的精度和可用数据量.

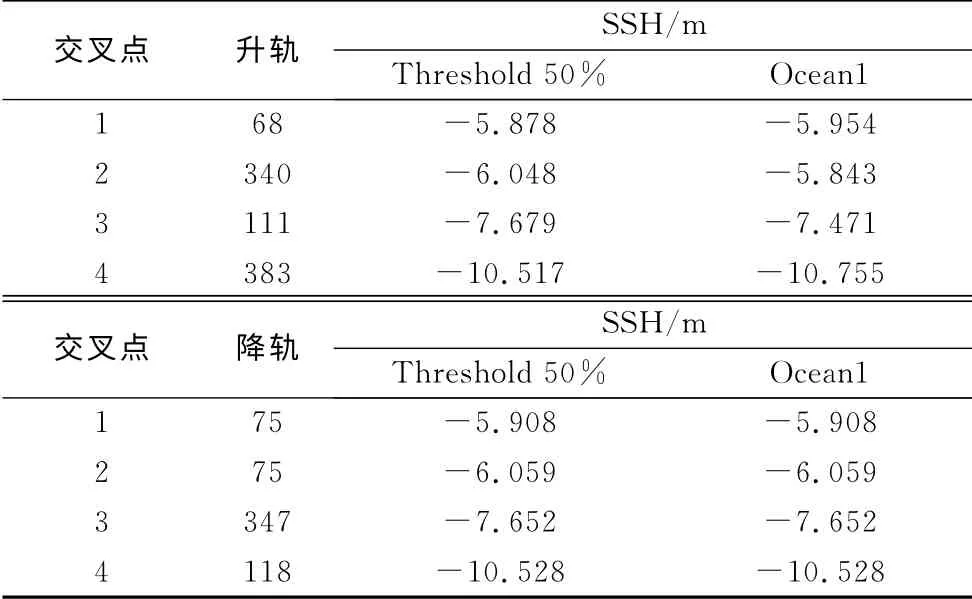
表4 研究区域四个交叉点海面高计算结果（第20周期）Tab.4 Retracked SSH of the 4crossover points in the study area（the 20th cycle）

4 结语

本文以海南近岸海域为例，利用Ocean1，Threshold，OCOG，Beta－5 等 波 形 重 构 算 法 对Envisat的18Hz测高波形数据进行重构研究，并对重构后海面高质量进行评价.由于海南周边海域复杂的海况及水深变化，该区域的研究结果对近岸海域的波形重构提供了有价值的参考.采用合适的波形重构算法能够大大提高近海测高海面高数据质量，Threshold 50%算法在研究区域的八条轨迹均取得较好的重构效果，重构后IMP 值最大可达59.0%，重构后海面高也更为光滑.重构后海面高中时变海面地形的标准差较小，交叉点处海面高的不符值也较小.今后应通过波形分类、重构算法改进等方法对近岸海域测高波形进行研究，并采用更为准确的湿对流层校正、潮汐校正等地球物理改正模型，进一步改善近岸海域卫星测高数据质量，提高近岸卫星测高数据的利用率.

［1］ 鲍李峰，陆洋，许厚泽.浅海区域Topex／Poseidon 测高卫星数据波形重构方法［J］.地球物理学报，2004，47（2）：216.BAO Lifeng，LU Yang，XU Houze.Waveform retracking of Topex／Poseidon altimeter in Chinese offshore ［J］.Chinese Journal of Geophysics，2004，47（2）：216.

［2］ CNES.Coastal and hydrology altimetry product（PISTACH）handbook（Issue 1.0）［M］.Paris：CNES，2010.

［3］ European Space Agency（ESA）.Envisat RA2／MWR product

handbook（Issue 2.1）［M］.Paris：ESA，2006.

［4］ 杨乐，林明森，张有广，等.中国近岸海域高度计JASON－1测量数据的波形重构算法研究［J］.海洋学报，2010，32（6）：91.YANG Le，LIN Mingsen， ZHANG Youguang，et al.Improving the quality of JASON－1 altimetry data by waveform retracking in coastal waters off China［J］.ActaOceanologica Sinica，2010，32（6）：91.

［5］ 郭金运，高永刚，常晓涛，等.近岸海域ENVISAT 卫星测高波形重定的Threshold 优化算法［J］.地球物理学报，2010，53（4）：807.GUO Jinyun，GAO Yonggang，CHANG Xiaotao，et al.Optimal threshold algorithm of ENVISAT waveform retracking over coastal sea［J］.Chinese Journal of Geophysics，2010，53（4）：807.

［6］ 常晓涛，李建成，郭金运，等.一种多前缘多阈值的波形重构算法［J］.地球物理学报，2006，49（6）：1629.CHANG Xiaotao，LI Jiancheng，GUO Jinyun，et al.A multileading edge and multi－threshold waveform retracker ［J］.Chinese Journal of Geophysics.2006，49（6）：1629.

［7］ GUO J Y，GAO Y G，HWANG C W，et al.A multisubwaveform parametric retracker of the radar satellite altimetric waveform and recovery of gravity anomalies over coastal oceans［J］.Science China Earth Sciences，2010，53：610.

［8］ HWANG C，GUO J Y，DENG X L，et al.Coastal gravity anomalies from retracked geosat／GM altimetry：improvement，limitation and the role of airborne gravity data［J］.Journal of Geodesy，2006，80：204.

［9］ GUO J Y，HWANG C W，CHANG X T，et al.Improved threshold retracker for satellite altimeter waveform retracking over coastal sea［J］.Progress in Natural Science，2006，16：732.

［10］ DENG X L.Improvement of geodetic parameter estimation in coastal regions from satellite radar altimetry［D］.Perth：Curtin University of Technology，2004.

［11］ DENG X L，FEATHERSTONE W，HWANG C W，et al.Estimation of contamination of ERS－2 and poseidon satellite radar altimetry close to the coasts of australia［J］.Marine Geodesy，2002，25（1）：249.

［12］ BAO L F，LU Y，WANG Y.Improved retracking algorithm for oceanic altimeter waveforms ［J］.Progress in Natural Science，2009，19：195.