基于小波技术的散乱点云自适应压缩算法

徐 工，程效军

（同济大学 测绘与地理信息学院，上海200092）

三维激光扫描系统的采样精度高（一般可以达到cm甚至mm级精度）［1］，尤其是随车载／机载扫描系统的不断成熟和完善，能够快速、准确地获取目标表面高密度点位信息，在获取数据的精度和速度方面有很大的优势，越来越广泛地应用于文物建筑的保护与修复、机械制造、数字城市建设海洋测深和环境监测等领域［1－2］.三维激光扫描获取的数据非常巨大，往往达到几十万甚至数百万的量级，庞大点云数据的存储、显示和传输占用了大量的时间和空间资源，而且大大降低了后续分析和处理的效率.因此，在保证一定精度的前提下，对海量点云数据进行压缩是点云后处理的必然选择［1－5］.

目前散乱点云数据压缩方法主要有两种：基于网格的压缩（mesh－based simplification）方法和基于点的 压 缩（points－based simplification）［5－8］方 法.前者要先建立点云数据的三角网格，然后将相同顶点的三角面片的最大法矢夹角［9］、压缩后点数和最大边界误差［10］、顶点合并的误差代价［11］等与相应的自定义阈值相比较，进行取舍，对网格进行简化.基于网格的压缩方法压缩效果比较好，但是构建网格，尤其是构建海量数据网格是一项复杂耗时的工作，效率低，而且没有固定的阈值选取准则，压缩效果具有一定的随意性.基于点的压缩方法是根据点云的空间拓扑关系计算对应的离散几何信息，如平均点距值［12］、包围盒点数［13］、均匀网格中心［14］、曲率［15］、非均匀网格特征点［4，12］等，根据信息量对点云进行精简处理.基于点的压缩方法直接简化点云，效率较高，但是压缩数据在细节和特征上的损失难以避免甚至难以控制［5］.

小波变换在时间（空间）域和频率域具有良好的局部化特性，通过小波函数的伸缩和平移，小波变换可以反映信号任意点处的细节信息，被誉为“数学显微镜”［16］.本文借助快速成型理论中的切片技术，将小波变换引入点云数据压缩中，提出一种基于小波技术的自适应压缩算法.通过与传统压缩方法的对比，说明该算法在实现快速压缩的同时能够兼顾点云的细节和特征信息，而且无需设置阈值或其他的参数，有助于实现压缩的自动化.

1 小波及小波变换理论

小波变换能够通过伸缩和平移小波函数，以不同的分辨率自适应地逼近信号.低分辨率下的小波变换可以描述信号更多的细节信息，而高分辨率下的小波变换能够反映出较大结构的轮廓.目前，小波变换已经广泛地应用于二维及高维图像和视频上，也有学者正在研究将小波变换应用于散乱点云处理方面［17］.

任一函数φ（t）∈L2（R），若其Fourier 变换满足

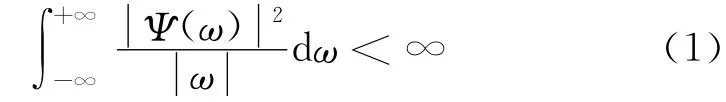
则φ（t）称为基本小波函数或小波母函数.其中，t为时间，ω为角频率，式（1）称为小波函数的可容许性条件.对小波母函数φ（t）进行平移和伸缩可得到小波基函数集

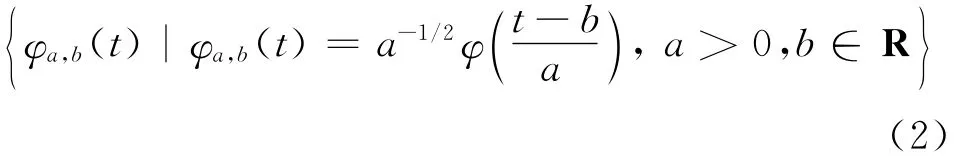
式中：a称为尺度伸缩因子，b称为时间平移因子.函数f∈L2（R）的连续小波变换（CWT）

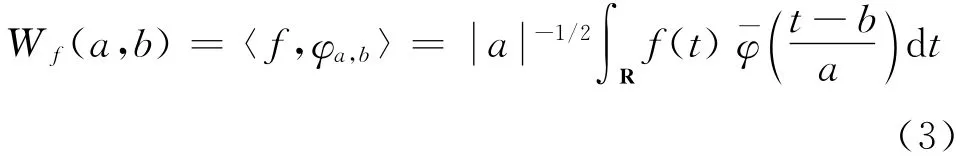
从式（3）中可以看出，小波变换为“恒Q滤波”，具有自适应性.尺度因子a决定了时（空）域和频域窗的大小，平移因子b决定了观测窗位置［16，18］.小波函数φa，b（t）中的尺度因子和平移因子决定了小波变换可以获取信号任意点处的细节信息，因而，小波系数的起伏与突变，能够自适应地识别信号的特征部位.鉴于小波系数的这种特征，本文将小波变换应用到点云数据压缩，以实现保留特征的点云自适应压缩.

2 点云特征的自适应识别

原始点云数据的特征保留是衡量点云数据压缩算法优劣的一个重要参数.以往的算法或是根据点的K近邻域［5］建立拓扑关系，计算点法矢、曲率与阈值的关系，判断特征点；或是构建网格，根据三角面片最大夹角与阈值的关系决定点的取舍［9］等.这些算法都依赖于阈值的选取，但是目前并不存在一个固定的阈值选取准则，因而特征点的提取结果具有一定的随意性.

小波系数能够反映相邻点的细节信息.若数据变化不大，即各个数据点相似，相应地由式（3）计算的小波系数也相似；当数据出现起伏变化时，对应的小波系数会发生改变，从而出现小波系数峰值，这说明小波峰值能够很好地反映点云数据的起伏变化.

假设有两组数据，一组变化平缓，近似是一条直线，另一组有起伏变化，如图1所示.从图1中可以看出，平缓数据的小波系数也是平缓的，没有峰值出现；起伏变化较大的一组数据，在发生变化的点处都出现了小波系数峰值.从仿真实例中可以明显看出小波系数的峰值可以自适应地探测数据的特征点.

图1 两组数据及其对应的小波系数Fig.1 Two sets of data and corresponding wavelet coefficients

3 算法概述

小波变换是一个一维的变换，为将小波变换引入到三维空间点云数据压缩中，需要对点云数据进行降维处理，首先借助切片技术将三维空间点云降维为二维平面点集，并按顺（逆）时针顺序对平面点集进行排序，然后对排序后的切片点云进行小波变换，获取小波系数峰值，并根据小波系数峰值自适应地选取需要保留的点.算法的流程如图2所示.

图2 算法流程图Fig.2 Algorithm flow chart

3.1 生成切片点云

三维激光扫描仪能够获取物体表面高密度的点云数据，沿物体的结构特征方向对点云数据进行切片，将落在切片上的数据投影到参考平面上，生成切片点云.经过切片处理后，三维空间散乱点云转化为能够反映物体轮廓形状的平面点集.

假 设 三 维 空 间 点 集p＝｛Pi＝（xi，yi，其 中Px＝｛x1，x2，…，xn｝，Py＝｛y1，y2，…，yn｝，Pz＝｛z1，z2，…，zn｝，分别表示X，Y，Z坐标，n表示点的数目.假设沿扫描坐标系的Z轴分割，分隔厚度为d，则第j层上的点即为Pz中满足条件zmin＋（j－1）d≤z＜zmin＋jd的点.从点集p中提取该层的点，并投影到相应的参考平面上，形成轮廓形状的切片点云.同样的方法，也可以得到沿X或Y轴分割的切片点云.以由地面激光扫描仪获取的华佗雕塑半身像的散乱点云数据为例，共69 189个点，沿Z轴做切片，得到的切片点云和其中某一单层切片如图3所示.

3.2 保留特征的点云自适应压缩

空间散乱分布的三维点云经过切片处理后，转化为以切片形式存在的二维平面点集.小波系数反映的是相邻若干数据的细节信息，从而需要对每个切片点云按照轮廓形状，以顺时针或逆时针的顺序进行排序，对排序后的数据进行小波变换，根据小波系数峰值选取需要保留的点.对图3c的切片保留特征的压缩结果如图4所示，切片点云采用的是顺时针排序.对所有的切片都进行相同的处理，可得到该点云数据的压缩结果.

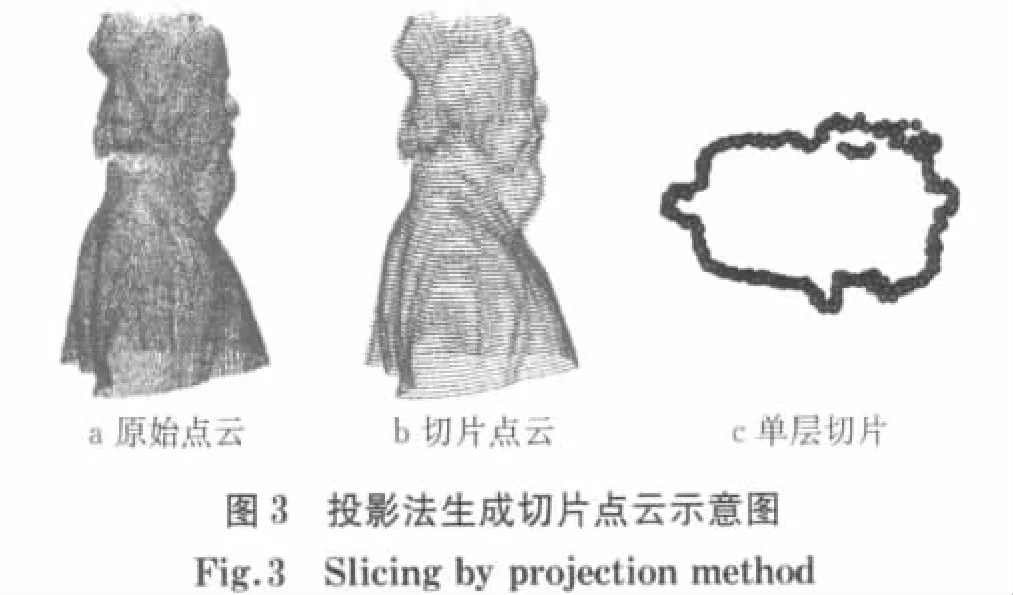
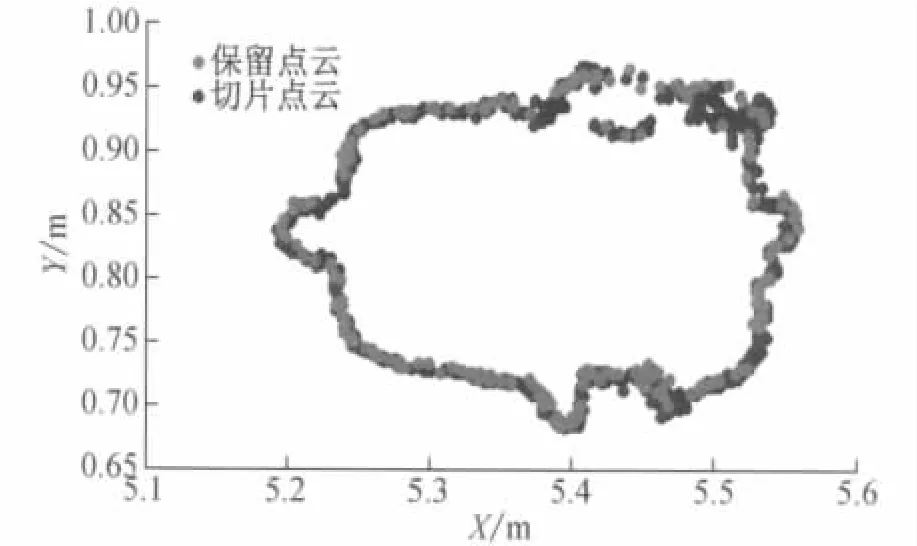
图4 单层切片点云和保留点云示意图Fig.4 Single slicing and point cloud retention

4 算例分析

点云数据压缩算法基本原则是在保证失真较小的情况下，最大限度地压缩点云数量，并在此基础上要求算法稳健、执行效率高、适应性强.一般而言，压缩率越高，保留的数据量越少，细节特征损失相对越多.下面通过实验讨论了切片分割厚度对算法的影响，以期获得最佳的切片分割厚度，并与传统压缩方法进行比较，说明本文算法在压缩率相同的情况下，能够保留更多的细节信息，失真较小.

4.1 分割厚度的选取

对原始点云做切片处理时，若切片的分割厚度d过大，投影时容易造成细节特征覆盖，损失数据特征信息；若分割厚度d过小，投影平面上的轮廓线容易出现空缺，在进行特征提取时，会将空缺的端点作为特征点保留，降低压缩率.因此切片厚度的选择和点云数据的采样间隔密切相关.综合考虑细节覆盖和轮廓线空缺问题，设计了多组实验，实验结果表明切片厚度按以下的方式选取时，可以较好地避免上述问题.

（1）若切片厚度小于2倍的采样间隔时，将落在该切片上的点全部投影到参考平面上.

（2）若切片厚度大于等于2倍采样间隔时，只取一半切片厚度的点投影到参考平面上，由于切片相对较薄，因而可以自由地选取一半切片厚度的点，可以是切片的上（或下）半部分，也可以是切片中间部分，对压缩效果影响不大.

图3所示的华佗半身像，采样间隔为0.3cm.表1是分隔厚度分别取为0.3，0.5，0.6，0.8，1.0，1.2，1.5cm 时，对应的压缩率和压缩时间统计，其中压缩时间是在Matlab平台上的运行时间.

表1 不同分割厚度对应的压缩率和压缩时间Tab.1 Reduction ratio and time in different split thickness

由表1可以看出，当分割厚度小于2倍的采样间隔时，压缩率随着分割厚度的增加而提高；当分割厚度大于等于2倍的采样间隔时，压缩率较高，其中分割厚度为0.8cm 时，压缩率出现的微小差异（量级为10－3）是由点云数据的散乱程度引起的，综合来说压缩率变化幅度较小，表明该算法对分割厚度的依赖相对较弱.

图5是针对上述实验对象，采用本文算法取不同分割厚度时对应的点云压缩效果.

通过图5 可以看出，当分割厚度取0.3，0.5，0.6，0.8，1.0cm 时，压缩效果均较好，较大程度地保留了特征信息，但是分割厚度为0.3，0.5cm 时，压缩率偏低，压缩时间较长，因此，分割厚度为0.6，0.8，1.0cm 时，压缩效果较为理想.

图6是利用图5中的压缩点云数据建立的网格模型.

由图6 可以看出，分割厚度小于等于1.0cm时，网格模型的细节和特征信息保留较好，当分割厚度大于1.2cm 时，眼睛、方巾的褶皱等部位的细节和特征信息损失严重.

通过表1、图5和6压缩效果分析可以得出，采用本文算法的压缩率较高，细节特征保留好，失真小，压缩时间快.综合压缩率和网格模型效果，建议分割厚度取为2～3倍的点云采样间隔.

4.2 与传统方法的比较

为了进一步说明本文算法，分别采用曲率估算法、均匀网格法、随机采样法对华佗半身像进行压缩.在压缩率均为86%时，三种方法点云压缩效果和网格模型分别如图7和8所示.

从图5～8可以看出，在压缩率均为86%时，从点云压缩效果和压缩后网格模型上都反映出本文算法在特征保留上具有明显的优势，在眼睛、鼻子、上嘴唇、方巾的褶皱等特征部位保留了更多的细节信息，压缩效果更为理想.

5 结语

本文借助快速成型理论中的切片技术，将小波变换引入点云数据压缩，提出基于小波技术的散乱点云自适应压缩算法.该算法实现简便、计算效率高，同时又最大限度地保留了细节和特征信息.通过实验表明切片的分割厚度选为采样间隔的2～3倍时，可以实现快速高质量的散乱点云压缩，与曲率估算法、均匀网格法、随机采样法的压缩效果进行对比，表明本文算法在特征保留上具有明显的优势，压缩效果更为理想，且无需设置阈值或其他参数，可以自适应地选取需要保留的细节和特征点，有助于实现压缩的自动化.

［1］ 吴航彬，刘春.三维激光扫描点云数据的空间压缩［J］.遥感信息，2006（2）：22.WU Hangbin，LIU Chun.Spatial compression of point cloud data from three dimension laser scanning［J］.Remote Sensing Information，2006（2）：22.

［2］ Schnabel R W，Moser S，Klein R.Fast vector quantization for efficient rendering of compressed point－clouds［J］.Computers ＆Graphics，2008，32：246.

［3］ 程效军，李伟英，张小虎.基于自适应八叉树的点云数据压缩方法研究［J］.河南科学，2010，28（10）：1300.CHENG Xiaojun，LI Weiying，ZHANG Xiaohu.Adaptive Octree－based data compression method for points cloud data［J］.Henan Science，2010，28（10）：1300.

［4］ 王秀英，刘锡国.逆向设计中点云数据处理技术的研究进展［J］.机械设计与制造，2009（9）：191.WANG Xiuying，LIU Xiguo.Development of research on point cloud data processing technology in reverse design［J］.Machinery Design ＆Manufacture，2009（9）：191.

［5］ 张鸿飞.基于散乱点云三维重建的关键技术研究［D］.上海：同济大学，2011.ZHANG Hongfei.Study of 3D reconstruction key technology based on scattered point cloud ［D］.Shanghai： Tongji University，2011.

［6］ Luebke D P.A developer’s survey of polygonal simplification algorithms［J］.IEEE Computer Graphics ＆Applications，2001，21（3）：24.

［7］ Cignoni P，Montani C，Scopigno R.A comparison of mesh simplification algorithms［J］.Computers ＆Graphics，1998，22（1）：37.

［8］ Erikson C.Polygonal simplification：an overview.Department of computer science［R］.Chapel Hill：University of North Carolina，1996.

［9］ 刘春，吴杭彬.基于真三维TIN 的三维激光扫描数据压缩方法［J］.武汉大学学报：信息科学版，2006，31（10）：908.LIU Chun，WU Hangbin.Compression method for three dimension laser scanning data based on 3D triangulated irregular network［J］.Geomatics and Information Science of Wuhan University，2006，31（10）：908.

［10］ Chen Y H，Ng C T，Wang Y Z.Data reduction in integrated reverse engineering and Rapid Prototyping［J］.International Journal of Computer Integrated Manufacturing，1999，2（12）：97.

［11］ 叶建辉，李德华.三维激光扫描数据的网格简化［J］.红外与激光工程，2002，31（6）：522.YE Jianhui，LI Dehua.Mesh simplification of 3D laser scanned data［J］.Infrared and Laser Engineering，2002，31（6）：522.

［12］ Weir D J，Milrou M J，Bradley C.Reverse engineering physical models employing wrap－around B－spline surfaces and quadrics［J］.Journal of Engineering Manufacture，1996，210（B）：145.

［13］ Sun W，Bradley C，Zhang Y F.Cloud data modeling employing a unified non－redundant triangle mesh ［J］.Computer Aided Design，2001，33（2）：183.

［14］ Martin R，Stroud I，Marshal A.Data reduction for reverse engineering［R］.［S.l.］：Computer and Automation Institute of Hungarian Academy of Science，1996.

［15］ 贺美芳.基于散乱点云数据的曲面重建关键技术研究［D］.南京：南京航空航天大学机电学院，2006.HE Meifang. Research on key technologies of surfaces reconstruction based on scattered point cloud data［D］.Nanjing：Nanjing University of Aeronautics and Astronautics Mechanical and Electrical Institute，2006.

［16］ 崔锦泰.小波分析导论［M］.西安：西安交通大学出版社，1995.CUI Jintai.An introduction to wavelet analysis［M］.Xi’an：Xi’an Jiaotong University Press，1995.

［17］ Liu C，Pei W.Wavelet transform based 3D scattered data processing in binocular micro stereovision system［J］.Key Engineering Materials，2005，291／292：673.

［18］ 李建平.小波分析信息传输基础［M］.北京：国防工业出版社，2004.LI Jianping.Wavelet analysis and information transmission［M］.Beijing：National Defence Industry Press，2004.